Задачи по риск менеджменту. ГР. Вариант 4 (определяется по последней цифре Вашего порядкового номера в списке Вашей группы в системе Элинос) Статистические методы оценки рисков
 Скачать 162.59 Kb. Скачать 162.59 Kb.
|
|
Вариант 4 (определяется по последней цифре Вашего порядкового номера в списке Вашей группы в системе «Элинос») 1. Статистические методы оценки рисков В таблице 1 представлены данные по объемам реализации компании. Рассчитайте вероятность каждого значения временного ряда, а также следующие показатели его динамики: - размах вариации - математическое ожидание - дисперсия - среднеквадратическое отклонение - коэффициент вариации Таблица 1
Рассчитаем абсолютные показатели вариации. Размах R=Xmax – Xmin=220-204 =16. Квартильный размах IQR=Q3 –Q1=215-204=11. Средняя арифметическая 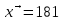 Среднее линейное отклонение: 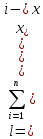 = = 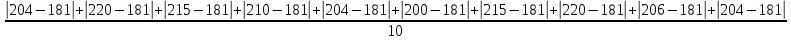 = 29 = 29Дисперсия 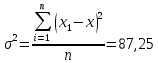 Cреднее квадратное отклонение 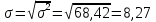 Относительные показатели вариации. Относительный размах 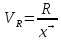 *100% = *100% = 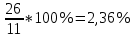 Относительное линейное отклонение 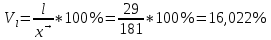 Коэффициент вариации 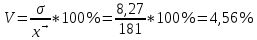 Можно сделать вывод, что вариация признана в совокупности не большая, совокупность можно считать – однородной по данному признаку. 2. Метод учета риска при расчете чистой приведенной стоимости NPV Первоначальные инвестиции компании в реализацию проекта составили 25 000 у. е. Безрисковая дисконтная ставка составляет 11 %. Вероятность возникновения денежных потоков составляет 90 %. Динамика чистых денежных потоков представлена в таблице 2. Рассчитайте эффективность проекта с учетом и без учета риска. Опишите недостатки данного метода учета рисков. Таблица 2
Чистая текущая стоимость: Поскольку NVP > 0, то проект следует принять к рассмотрению. Индекс рентабельности: Поскольку PI > 1, то проект следует принять к рассмотрению. Внутренняя норма прибыли инвестиции. Под внутренней нормой прибыли инвестиции (RR-синонимы: внутренняя доходность, внутренняя окупаемость) понимают значения коэффициента дисконтирования r, при котором NPV проекта равен нулю: Срок окупаемости – это минимальный временной интервал (от начала осуществления проекта), за пределами которого интегральный эффект становится и в дальнейшем остается неотрицательным.
В нашем случае капитальные вложения равны 25000 ден. ед. По таблице видно, что 25000 ден. ед. покроются суммарными результатами после 4 года. Это результат примерный, только в годах. Для уточнения периода окупаемости рассчитаем, за какой период будут покрыты все инвестиционные затраты после 4 года. Нарастающий DICt-PV4 = 25000-9841.123=15158.877 Интегральный результат за 5 год: PV5 = 18990.442 ден.ед. за 365 дней. DРР2=15158.877/18990.442*365=291 дней. Следовательно, срок окупаемости проекта составит: DРP=DРР1+DРР2 = 4 года + 291 день. 3. Метод построения «дерева решений» Международная нефтяная компания должна принять решение о бурении скважины. В начальный момент времени t=0 необходимо потратить $5 млн на проведение трехмерной сейсмической разведки, которая увеличивает шансы успешной разработки. Вероятность положительных результатов разведки составляет 80 %, отрицательных – 20 %. Если в результате разведки будет выяснено, что потенциал скважины достаточно высок, то компания инвестирует еще $ 40 млн на бурение (t=1). Вероятность того, что скважина все-таки окажется сухой составляет 10 %. В случае открытия месторождения компания сможет получать прибыль около $ 80 млн в год при оптимистическом сценарии (вероятность 10 %), $ 50 млн – при наиболее вероятном развитии событий (вероятность 85 %) и $ 20 млн – при наихудшем сценарии (вероятность 5 %). Срок добычи нефти в случае открытия месторождения составляет 3 года. Ставка цены капитала компании при реализации данного проекта составляет 10 % Постройте дерево решений, рассчитайте финансовый результат каждого варианта и определите целесообразность реализации проекта. Построим дерево решений
Рассчитаем чистую приведенную стоимость каждого варианта по формуле 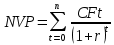
Чистая текущая стоимость: Поскольку NVP > 0, то проект следует принять к рассмотрению. Индекс рентабельности: Поскольку PI > 1, то проект следует принять к рассмотрению. Внутренняя норма прибыли инвестиции. Под внутренней нормой прибыли инвестиции (RR-синонимы: внутренняя доходность, внутренняя окупаемость) понимают значения коэффициента дисконтирования r, при котором NPV проекта равен нулю: Срок окупаемости – это минимальный временной интервал (от начала осуществления проекта), за пределами которого интегральный эффект становится и в дальнейшем остается неотрицательным.
4. Метод анализа чувствительности проекта Первоначальные инвестиции компании в реализацию проекта составили $ 80 000. Норма дисконта по проекту составляет 10 %. Постоянные затраты производства - $1 000 в год. Переменные затраты на единицу продукции равны $ 14. Планируемая цена реализации – $ 39. Объем реализации - 1 200 шт. Определите чувствительность чистой приведенной стоимости NPV проекта к изменению постоянных и переменных затрат на 10 %. Управлению каким из этих показателей компании необходимо уделить наибольшее внимание? Рассчитайте критический объем производства без учета первоначальных инвестиций и дисконтирования. Выручка нетто: 46800$ Издержки 17800 $ В том числе переменные 16800$ Маржинальной прибыли 30000 $ Общей прибыли 29000 $ Рентабельность продаж 61,97% Точка безубыточности составляет 40,00 ед. 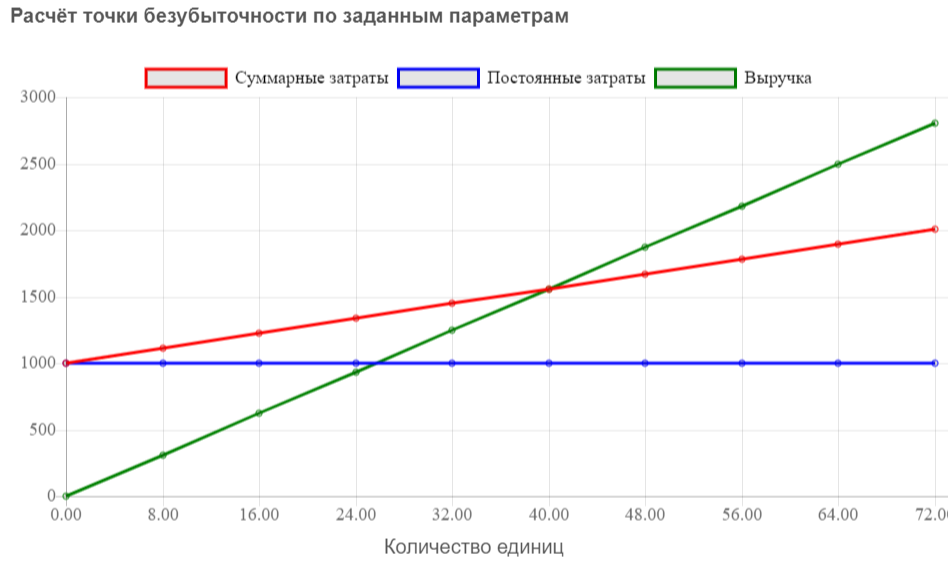 Дисконтированные денежные потоки по годам. Коэффициент дисконтирования:
Чистая текущая стоимость: Поскольку NVP > 0, то проект следует принять к рассмотрению. Индекс рентабельности: Поскольку PI < 1, то проект следует отклонить от рассмотрения. Внутренняя норма прибыли инвестиции. Под внутренней нормой прибыли инвестиции (RR-синонимы: внутренняя доходность, внутренняя окупаемость) понимают значения коэффициента дисконтирования r, при котором NPV проекта равен нулю: Срок окупаемости – это минимальный временной интервал (от начала осуществления проекта), за пределами которого интегральный эффект становится и в дальнейшем остается неотрицательным.
В нашем случае капитальные вложения равны 0 ден. ед. По таблице видно, что 0 ден. ед. покроются суммарными результатами после 0 года. Это результат примерный, только в годах. Для уточнения периода окупаемости рассчитаем, за какой период будут покрыты все инвестиционные затраты после 0 года. Нарастающий DICt-PV0 = 0-0=0 Интегральный результат за 1 год: PV1 = 42545.455 ден.ед. за 365 дней. DРР2=0/42545.455*365=0 дней. Следовательно, срок окупаемости проекта составит: DРP=DРР1+DРР2 = 0 года + 0 день. Определение предельного значения изменения дохода. В ситуации, когда инвестиционный проект будет иметь интегральную точку безубыточности, NPV будет равен нулю. Дисконтированные денежные потоки по годам. Коэффициент дисконтирования:
Чистая текущая стоимость: Поскольку NVP > 0, то проект следует принять к рассмотрению. Индекс рентабельности: Поскольку PI < 1, то проект следует отклонить от рассмотрения. Внутренняя норма прибыли инвестиции. Под внутренней нормой прибыли инвестиции (RR-синонимы: внутренняя доходность, внутренняя окупаемость) понимают значения коэффициента дисконтирования r, при котором NPV проекта равен нулю: Срок окупаемости – это минимальный временной интервал (от начала осуществления проекта), за пределами которого интегральный эффект становится и в дальнейшем остается неотрицательным.
В нашем случае капитальные вложения равны 0 ден. ед. По таблице видно, что 0 ден. ед. покроются суммарными результатами после 0 года. Это результат примерный, только в годах. Для уточнения периода окупаемости рассчитаем, за какой период будут покрыты все инвестиционные затраты после 0 года. Нарастающий DICt-PV0 = 0-0=0 Интегральный результат за 1 год: PV1 = 46800 ден.ед. за 365 дней. DРР2=0/46800*365=0 дней. Следовательно, срок окупаемости проекта составит: DРP=DРР1+DРР2 = 0 года + 0 день. Определение предельного значения изменения дохода. В ситуации, когда инвестиционный проект будет иметь интегральную точку безубыточности, NPV будет равен нулю. 5. Выбор оптимальной стратегии Минимальный гарантированно устойчивый спрос на продукцию предприятия составляет 500 шт. Устойчивый сбыт на конкретный год составляет 1 000 шт. Возможная сверх устойчивого спроса реализация составляет 2 000 шт. Маловероятный, но потенциально возможный спрос составляет 4 000 шт. Цена реализации продукции составляет 10 у. е. Постоянные расходы равны 100 у. е., переменные расходы на единицу продукции – 2 у. е. Руководство предприятия планирует три стратегии производства продукции: S1 = 1 000 шт., S2 = 2 000 шт., S3 = 4 000 шт. Определите оптимальную стратегию для данного предприятия на основе критерия Вальда, Сэвиджа и Гурвица. Выберите показатель Гурвица, близкий к пессимистическому сценарию. Прибыль рассчитаем как разницу между выручкой от реализации и затратами: П = В - З Выручка от реализации при каждом варианте размера спроса определяется как произведение цены и объема реализации (спроса): В = d * P Затраты на производство продукции рассчитаем по формуле: З = FC + vc * Q Полученные данные занесем в таблицу и определим максимальные и минимальные значения прибыли при различных вариантах объема производства, а также максимальные значения прибыли при каждом варианте объема спроса на продукцию. З = 100+2*500 = 1100 З = 100+2*1000 = 2100 З = 100+2*2000 = 4100 З = 100+2*4000=8100 Выбор оптимальной стратегии по критерию Гурвица. При выборе решения из двух крайностей, связанных с пессимистической стратегией по критерию Вальда и чрезмерным оптимизмом по критерию Сэвиджа можно выбрать некоторую промежуточную позицию, граница которой определяется показателем пессимизма-оптимизма g, находящимся в пределах 0 ≤ g ≤ 1. Такой критерий называется критерием Гурвица. Как частный случай при g=1 из него следует максиминный критерий Вальда, а при g=0 – минимаксный критерий Сэвиджа. В соответствии с критерием Гурвица для каждой стратегии выбирается линейная сумма взвешенных минимального и максимального выигрышей по формуле: Gi = g * Пmin + (1-g) * Пmax где Пmin – минимальный размер прибыли (убытков) от спроса (продаж) для каждого объема производства (табл. 6.1); Пmax – максимальный размер прибыли (убытков) от спроса (продаж) для каждого объема производства (табл. 6.1). Положим g=0,4 (близкий к оптимистическому критерий) и рассчитаем Gi для трех стратегий Q1, Q2, Q3 G1 = 0,4 * (50) + (1-0,4) * 550 = 350 у.е. G2 = 0,4 * (-50) + (1-0,4) * 950 = 550 у.е. G3 = 0,4 * (-150) + (1-0,4) * 1350 = 750 у.е. Затем выбирается такая стратегия, для которой величина Gi получается наибольшей. В нашем примере Gmax = G3, следовательно Qопт = Q3. | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
