№
|
Вопросы
|
Варианты ответов
|  106. 106.
|
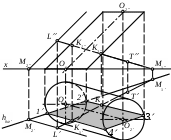
Прямая LT пересекает поверхность призмы А1В1С1А2В2С2. В направлении на плоскость 2 невидимым будет следующий участок прямой LT:
|
1) К12
2) К1К2
3) 1К1
4) 12
5) 1К2
|  107. 107.
|
Для построения точек встречи прямой LT с поверхностью конуса построено сечение S12. Это сечение образовано
|
1) вспомогательной плоскостью, проходящей через прямую LT и центр основания О
2) вспомогательной плоскостью общего положения, проходящей через прямую LT и вершину конуса S
3) вспомогательной плоскостью частного положения, проходящей через вершину S и центр основания О
4) вспомогательной плоскостью частного положения, проходящей через прямую LT
5) вспомогательной плоскостью частного положения, проходящей через вершину S
|   108. 108.
|
Для построения точек встречи прямой LT с поверхностью цилиндра построено сечение 1234. Это сечение образовано
|
1) вспомогательной плоскостью, проходящей через ось цилиндра О1О2 и точку L
2) вспомогательной плоскостью общего положения, проходящей через прямую LT и центр основания О1
3) вспомогательной плоскостью частного положения, проходящей через прямую LT
4) вспомогательной плоскостью общего положения, проходящей через прямую LT и прямую, параллельную оси цилиндра
5) вспомогательной плоскостью частного положения, проходящей ось цилиндра О1О2
|
№
|
Вопросы
|
Варианты ответов
| 109. |
Развертка поверхности представляет собой
|
1) фигуру, представляющую собой поверхность геометрического тела в натуральную величину
2) проекцию геометрического тела, выполненную при помощи параллельного ортогонального проецирования
3) определение геометрических размеров фигуры путем алгебраических вычислений
4) фигуру, образуемую при совмещении поверхности геометрического тела с плоскостью чертежа
5) проекцию геометрического тела, полученную в натуральную величину
|  110. 110.
|
Развертка поверхности пирамиды SABC построена методом треугольников, который заключается в том, что
|
1) пирамида последовательно вращается вокруг ребер до совмещения граней с плоскостью чертежа
2) поверхность пирамиды рассекается плоскостью, перпендикулярной ребрам
3) определяется натуральная величина ребер пирамиды
4) по трем известным сторонам в плоскости чертежа строятся треугольники, составляющие грани пирамиды SABC
5) одним из методов преобразования эпюра положение пирамиды преобразуется из общего в частное
|
№
|
Вопросы
|
Варианты ответов
| 111. |
Для построения развертки призмы методом нормального сечения
|
1) поверхность призмы необходимо рассечь вспомогательной плоскостью, перпендикулярной ее ребрам
2) поверхность призмы предварительно разбивается на треугольники
3) поверхность призмы совмещается с плоскостью чертежа путем вращения вокруг ее ребер
4) через ребра проводятся вспомогательные плоскости частного положения
5) поверхность призмы аппроксимируется другой многогранной поверхностью
|  112. 112.
|
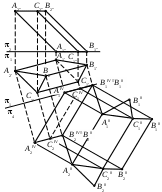
При построении развертки призмы А1В1С1А2В2С2 точка А10 была найдена
|
1) на прямой, проведенной из А1IV перпендикулярно В1IVB2IV, на расстоянии, равном А1В1, от проекции ребра В1IVB2IV
2) в пересечении прямой, проведенной параллельно А1IVВ1IV, и прямой, проведенной из А1IV перпендикулярно В1IVB2IV
3) в пересечении прямой, проведенной параллельно А1IVВ1IV, и дуги окружности, проведенной из В1IV радиусом, равным А1В1
4) в пересечении перпендикуляра, проведенного из точки А1IV, и дуги окружности, проведенной из В1IV радиусом, равным А1IVВ1IV
5) в пересечении следа плоскости вращения точки А и дуги окружности, проведенной из В1IV радиусом, равным А1В1
| 113. |
Развертка поверхности прямого кругового конуса представляет собой
|
1) сектор, радиус которой равен длине образующей конуса
2) сегмент окружности, радиус которой равен длине образующей конуса
3) фигуру, ограниченную синусоидой и двумя отрезками, исходящими из одной точки
4) прямоугольник, высота которого равна длине образующей конуса
5) равносторонний треугольник, сторона которого равна длине образующей конуса
|
№
|
Вопросы
|
Варианты ответов
| 114. |
Поверхности конуса и цилиндра относятся к
|
1) неразвертываемым поверхностям
2) развертываемым поверхностям
3) условно развертываемым поверхностям
4) аппроксимируемым поверхностям
5) приближенно развертываемым поверхностям
|  115. 115.
|
Найдите верный алгоритм построения развертки наклонного кругового конуса.
|
1) В конус вписана пирамида, ребра которой равны отрезкам образующих конуса, и методом треугольников построена развертка поверхности этого многогранника; построенные на развертке вершины основания пирамиды соединены плавной кривой линией.
2) В конус вписана пирамида, ребра которой равны отрезкам образующих конуса, и методом треугольников построена развертка поверхности этого многогранника; построенные на развертке вершины основания пирамиды соединены отрезками прямых.
3) В конус вписана призма, и методом нормального сечения построена развертка поверхности этого многогранника; построенные на развертке вершины основания пирамиды соединены плавной кривой линией.
4) В конус вписана пирамида, ребра которой равны отрезкам образующих конуса, и методом раскатки построена развертка поверхности этого многогранника; построенные на развертке вершины основания пирамиды соединены плавной кривой линией.
5) В конус вписана пирамида, ребра которой равны отрезкам образующих конуса, и методом нормального сечения построена развертка поверхности этого многогранника; построенные на развертке вершины основания пирамиды соединены плавной кривой линией.
|
№
|
Вопросы
|
Варианты ответов
|   116. 116.
|
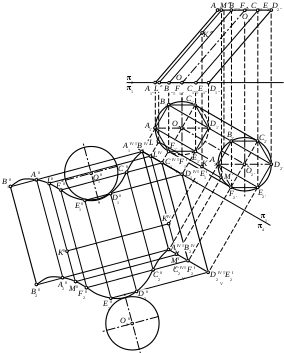
Точка К нанесена на поверхность развертки
цилиндра следующим образом.
| | |
|
1) На развертку нанесена образующая LM, и в пересечении этой образующей со следом плоскости вращения точки К найдена точка К0.
2) Из точки КIV проведен перпендикуляр к плоскости 4, и в пересечении с образующей LM найдена точка К0.
3) Она совпадает с проекцией точки К на плоскости 4.
4) В цилиндр вписана призма, построена развертка ее поверхности и на поверхности развертки найдено положение точки К.
5) В пересечении перпендикуляров, проведенных из КIV и М0.
|
№
|
Вопросы
|
Варианты ответов
|  117. 117.
|
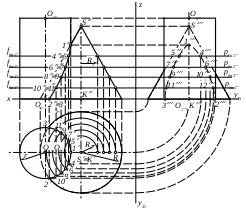
Линией пересечения прямой четырехугольной призмы D1Е1F1G1D2E2F2G2 и треугольной пирамиды SABC является
|
1) два плоских многоугольника 1-2-3 и 4-5-7-6-8-4
2) пространственная замкнутая ломаная линия 1-2-3-4-5-7-6-8-4
3) треугольник 123
4) треугольник 123 и пространственная замкнутая ломаная линия 4-5-7-6-8-4
5) пространственная замкнутая ломаная линия 4-5-7-6-8-4
|   118. 118.
|
Линия пересечения прямого кругового цилиндра и прямого кругового конуса построена
|
1) методом вспомогательных секущих сфер
2) методом вспомогательных образующих
3) методом вспомогательных секущих плоскостей (в данном случае – горизонтальных)
4) методом вспомогательных секущих плоскостей (в данном случае – фронтальных)
5) при помощи сетки проф. Д.Г.Ананова
|
№
|
Вопросы
|
Варианты ответов
| 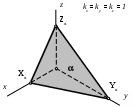 119. 119.
|
Плоскость изображена в
|
1) прямоугольной изометрической проекции
2) прямоугольной диметрической проекции
3) косоугольной фронтальной изометрической проекции
4) косоугольной горизонтальной изометрической проекции
5) косоугольной фронтальной диметрической проекции
| 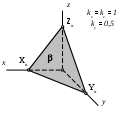 120. 120.
|
Плоскость изображена в
|
1) прямоугольной изометрической проекции
2) прямоугольной диметрической проекции
3) косоугольной фронтальной изометрической проекции
4) косоугольной горизонтальной изометрической проекции
5) косоугольной фронтальной диметрической проекции
|
Зав. кафедрой, проф. Бобин Н.Е.
Составитель, доц. Талалай П.Г.
|
 Скачать 1 Mb.
Скачать 1 Mb.