|
|
НАЧ10. Варианты ответов 1
№
|
Вопросы
|
Варианты ответов
|  101. 101.
|
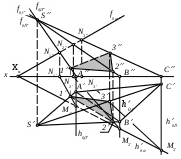
Для построения сечения пирамиды SABC плоскостью использован
|
1) способ «граней», т.е. найдены линии пересечения граней пирамиды с плоскостью
2) способ «ребер», т.е. найдены точки встречи ребер пирамиды с плоскостью
3) метод нормального сечения, т.е. пирамида рассечена вспомогательной плоскостью, перпендикулярной ее ребрам
4) способ треугольников
5) метод раскатки
| 102. |
В общем случае, построение сечения линейчатой поверхности (конуса или цилиндра) проводится путем
|
1) аппроксимации ее поверхности многогранной (пирамидальной или призматической)
2) проведения вспомогательных секущих плоскостей
3) замены данных плоскостей проекций на плоскости, по отношению к которым линейчатая поверхность будет занимать некоторое частное положение
4) совмещения ее поверхности с плоскостью проекций
5) преобразования проекций
|  103. 103.
|
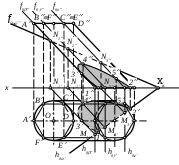
В направлении на плоскость 2 невидимой частью сечения поверхности цилиндра плоскостью будет кривая
|
1) 1-3
2) 1-3-4-5-2
3) 3-4-5-2
4) 4-5-2
5) 5-2
|
№
|
Вопросы
|
Варианты ответов
|  104. 104.
|
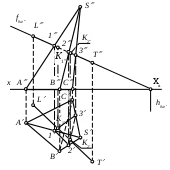
Определите правильный алгоритм нахождения точек пересечения К1 и К2 прямой LT с поверхностью пирамиды SABC.
|
1) Через прямую проведена вспомогательная фронтально-проецирующая плоскость , построено сечение 123 этой вспомогательной плоскостью и найдены искомые точки в пересечении прямой LT с контурами построенного сечения.
2) Через ребра пирамиды проведены вспомогательные плоскости, построено сечение 123 и найдены искомые точки в пересечении прямой LT с контурами построенного сечения.
3) Построена линия пересечения плоскости с пирамидой SABC, в плоскости выбрана произвольная прямой LT и найдены искомые точки в пересечении прямой LT с построенной линией пересечения.
4) Определены грани, в которых прямая LT пересекает поверхность пирамиды SABC и построены точки пересечения прямой LT с этими гранями.
5) В гранях пирамиды SABC построены вспомогательные прямые 12, 23 и 34 и найдены точки пересечения этих прямых с заданной прямой LT.
| 105. |
В чем заключается общность способов построения точек пересечения прямой линии с поверхностью многогранника и прямой линии с плоскостью.
|
1) Применяется один из способов преобразования проекций.
2) Через прямую и ребра пирамиды проводится вспомогательная секущая плоскость частного положения.
3) Применяется способ вспомогательных секущих плоскостей, проходящих через ребра многогранника.
4) Вводится дополнительная плоскость проекций, перпендикулярная плоскости 1 или 2.
5) Через прямую проводится вспомогательная плоскость (частного положения) и строится фигура, образуемая в пересечении этой плоскости с заданным геометрическим элементом.
| |
|
|
 Скачать 1 Mb.
Скачать 1 Mb.