конечные графы. Вершинами графа, элементы множества e называются ребрами графа а пара (V, e ), т е. множество вершин и ребер графа называется графом. Если две вершины графа соединены ребром, то такие вершины называются смежными
 Скачать 350.58 Kb. Скачать 350.58 Kb.
|
|
Теорема о сумме степеней вершин двудольного графа . Суммы степеней вершин двудольного графа равны . Доказательство . Пусть 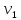 , , 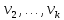 – вершины одной доли , а – вершины одной доли , а 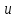 , , 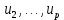 – вершиныдругой доли . Тогда из одной доли выходит d( – вершиныдругой доли . Тогда из одной доли выходит d(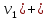 d( d(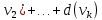 ребер , а из другой ребер , а из другой d( 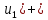 d( d(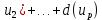 ребер . Равенство сумм следует из того , что это одни и те же ребра . ребер . Равенство сумм следует из того , что это одни и те же ребра .Определение . Граф называется n – дольным , если все его вершины можно разбить на n частей ( долей ) так , что каждое ребро будет иметь свои концы в разных долях . Определение . Связный граф , в котором отсутствуют циклы называется деревом . Граф , в котором отсутствуют циклы называется лесом . В любом дереве есть висячая вершина. Доказательство .Предположим противное . Рассмотрим произвольную вершину 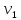 и и Перейдем из нее по любому ребру ( 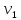 , , 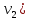 в вершину в вершину  . Поскольку степень вершины . Поскольку степень вершины  не меньше двух , то из нее по новому ребру можно в вершину не меньше двух , то из нее по новому ребру можно в вершину  и т.д. Но число вершин в графе Gконечно .Поэтому мы в конце концов придем в одну из вершин , в которой уже были . Это означает существование цикла , что противоречит условию . и т.д. Но число вершин в графе Gконечно .Поэтому мы в конце концов придем в одну из вершин , в которой уже были . Это означает существование цикла , что противоречит условию .Каждое дерево имеет висячую вершину .Удалим висячую вершину 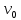 из дерева из дерева G вместе с ребром , выходящим из  будет связным ,и в нем нет циклов , то есть будет связным ,и в нем нет циклов , то есть  – дерево .Продолжим эту процедуру для – дерево .Продолжим эту процедуру для  и построим и построим  . В итоге . В итоге придем к дереву , состоящему из одной вершины . Получаем равенство m=n-1 , где m – число ребер . а n – число вершин дерева . таким образом в любом дереве число ребер будет на единицу меньше числа вершин . Задача . В связном графе , у которого число ребер на единицу меньше числа вершин нет циклов . Р     ешение . Предположим противное : Граф G содержит цикл .поставим в соответствие каждой вершине цикла ребро цикла , которое выходит из этой вершины , если проходить цикл по часовой стрелке . Для каждой вершины , не принадлежащей циклу , выделим ешение . Предположим противное : Граф G содержит цикл .поставим в соответствие каждой вершине цикла ребро цикла , которое выходит из этой вершины , если проходить цикл по часовой стрелке . Для каждой вершины , не принадлежащей циклу , выделим  цепь , соединяющую . вершину с циклом и содержащую наименьшее цепь , соединяющую . вершину с циклом и содержащую наименьшеечисло ребер .( Если таких цепей будет несколько , возьмем любую ) . Каждой такой вершине поставим в соответствие ребро выделенной цепи идущее от вершины к циклу . Таким образом каждой вершине графа будет поставлено в соответствие ребро , причем различным вершинам будут поставлены в соответствие различные ребра .Поэтому в графе ребер будет не меньше , чем вершин . Теорема . Связный граф , имеющий n вершин и mребер , является деревом тогда и только тогда , когда m=n-1. Теорема . Для графа G , имеющего n вершин и mребер следующие утверждения эквивалентны . •G- дерево ; • G – связный граф и m=n-1; •G – граф без циклов и m=n-1; •Любые две несовпадающие вершины графа G соединяет единственная простая цепь . Импликации G- дерево 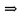 G – связный граф и m=n-1⇒G – граф без циклов и m=n-1 уже доказаны .Докажем импликацию : G – граф без циклов и m=n-1⇒Любые две несовпадающие вершины графа G соединяет единственная простая цепь . G – связный граф и m=n-1⇒G – граф без циклов и m=n-1 уже доказаны .Докажем импликацию : G – граф без циклов и m=n-1⇒Любые две несовпадающие вершины графа G соединяет единственная простая цепь .Доказательство . Предположим , что для некоторых вершин aи b путь из aв b не является единственным .Пусть существуют два различных пути : 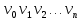 длины n длины n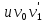 … …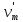 длины m , где a= 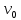 и b= и b=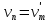 . В каждом пути должна существовать первая вершина , начиная с которой соответствующие вершины не совпадают , скажем . В каждом пути должна существовать первая вершина , начиная с которой соответствующие вершины не совпадают , скажем 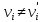 и ив каждом пути должна существовать точка , начиная с которой вершины опять одни и те же . Скажем 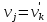 . Тогда . Тогда 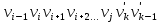 … …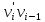 , поэтому граф G не является деревом . , поэтому граф G не является деревом .Докажем импликацию : Любые две несовпадающие вершины графа G соединяет единственная простая цепь ⇒G- дерево . Доказательство . Предположим , что G не является деревом . Тогда либо G не является связным , либо содержит цикл . Если граф G не связный, то существуют вершины a, b  G , для которых не существует пути из aв b .Значит не существует и единственного пути из aв b . Если же содержит цикл G , для которых не существует пути из aв b .Значит не существует и единственного пути из aв b . Если же содержит цикл 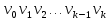 , то как , то как 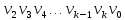 , так и , так и 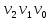 являются путями из 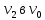 .значит из a= .значит из a= в b= в b=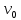 существует не единственный путь . существует не единственный путь .Пусть G – связный граф. Эксцентриситетом вершины vназывается расстояние от вершины V до самой дальней от v вершины . Центральной вершиной графа называется вершина , имеющая наименьший эксцентриситет . Множество центральных вершин графа называется центром графа . Теорема . Центр дерева состоит из одной , или двух смежных вершин . Доказательство . Пусть G –дерево . Самой дальней от любой его вершины будет некоторая висячая вершина . Если из дерева удалить все висячие вершины , то Эксцентриситет каждой вершины в новом графе станет на единицу меньше , чем в старом . Поэтому центральными вершинами в новом графе останутся те же вершины , что и в старом .Будем продолжать процесс удаления висячих вершин до тех пор , пока не придем к деревьям с одной или двумя вершинами . Так как на каждом шаге центральные вершины получающегося графа совпадают с центральными вершинами преобразуемого графа , то оставшиеся вершины будут центральными для исходного графа . Определение . Наибольшее из расстояний между вершинами графа называется диаметром графа и обозначается d(G) . Определение .Подграф графа G , содержащий все вершины графа , называется остовным . Если остовной граф является деревом , то он называется остовным деревом . Остовное дерево , имеющее минимальную суммарную длину ребер называется минимальным остовным деревом . Теорема . У каждого связного графа существует подграф , который является остовным деревом . Доказательство . Пусть G содержит цикл , если ребро { 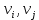 } входит в цикл то } входит в цикл то Существуют два пути из 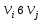 . значит ребро { . значит ребро {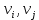 } можно из цикла удалить , а путь из вершины } можно из цикла удалить , а путь из вершины 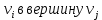 будет существовать . Пусть a иb – любые вершины в графе G . будет существовать . Пусть a иb – любые вершины в графе G .Так как граф G связен , то существует путь из a вb . Если ребро { 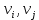 } удалено . то все равно существует путь из a вb .Удалим ребро { } удалено . то все равно существует путь из a вb .Удалим ребро {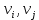 } из G и , если оставшийся граф все еще содержит цикл , удалим другое ребро , используя ту же процедуру . Процесс } из G и , если оставшийся граф все еще содержит цикл , удалим другое ребро , используя ту же процедуру . Процесспродолжим до тех пор . пока все циклы не будут удалены . В результате получим связный граф  без циклов , то есть дерево . без циклов , то есть дерево .Заметим . что вообще говоря эта процедура не однозначна . Пример :      • • • • • • • • • • • •• • • • • • • • • Диаметральной цепью называется цепь наименьшей длины между двумя вершинами , расстояние между которыми равно диаметру графа . Определение . Связный граф , в котором существует цикл , проходящий через все ребра графа называется эйлеровым . Сам цикл также называется эйлеровым . Теорема Эйлера . Связный граф является эйлеровым тогда и только тогда , когда степень каждой его вершины четна . Доказательство . Пусть G имеет эйлеров цикл . Граф связен так как каждая вершина принадлежит циклу . Эйлеров цикл проходит через v, он вносит 2 в степень v . Поэтому степень v четная . Докажем . что каждый связный граф , у которого степени вершин четные имеет эйлеров цикл . Доказательство индукцией по числу вершин . Пусть n 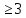 . Предположим , что . Предположим , что Каждый связный граф , имеющий менее kвершин , все вершины которого имеют четную степень , содержит эйлеров цикл . Пусть G – связный граф , содержит kвершин , степени которых четные .Пусть 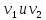 – вершины графа G. Существует путь из – вершины графа G. Существует путь из 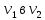 . Поскольку . Поскольку степень  – четная существует неиспользованное ребро по которому можно продолжить путь .Так как граф конечный , то путь в конце концов должен вернуться в – четная существует неиспользованное ребро по которому можно продолжить путь .Так как граф конечный , то путь в конце концов должен вернуться в 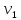 и эйлеров цикл и эйлеров цикл  можно считать построенным . Если можно считать построенным . Если 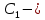 эйлеров цикл для G , то доказательство закончено .Если нет , то пусть эйлеров цикл для G , то доказательство закончено .Если нет , то пусть  подграф графа G , полученный удалением всех ребер , принадлежащих подграф графа G , полученный удалением всех ребер , принадлежащих . Поскольку . Поскольку  содержит четное число ребер , инцидентных каждой вершине , каждая вершина подграфа содержит четное число ребер , инцидентных каждой вершине , каждая вершина подграфа  имеет четную степень .Пусть e ребро графа имеет четную степень .Пусть e ребро графа  , ,и 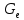 – компонента графа – компонента графа  , содержащая e . Так как , содержащая e . Так как  имеет менее , чем kвершин и у имеет менее , чем kвершин и у каждой вершины графа  четная степень , граф четная степень , граф  имеет эйлеров цикл . Обозначим его имеет эйлеров цикл . Обозначим его 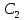 . У . У  и и 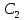 имеется общая вершина . Обозначим ее a .Теперь можно продолжить эйлеров цикл , начиная его в a . Пройти имеется общая вершина . Обозначим ее a .Теперь можно продолжить эйлеров цикл , начиная его в a . Пройти , вернуться в a , затем пройти , вернуться в a , затем пройти 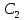 и вернуться в и вернуться вa . Продолжаем использовать этот процесс , расширяя наш эйлеров цикл , пока не получим эйлеров цикл для G . Определение. Пусть G=G(V ,E) –граф . Путь, который включает каждое ребро графа G только один раз называется эйлеровым путем . В этом случае говорят , что граф имеет эйлеров путь . Эйлеров путь . не являющийся эйлеровым циклом будем называть собственным эйлеровым путем . Теорема .Граф имеет собственный эйлеров путь тогда и только тогда, когда он связен и ровно две его вершины имеют нечетную степень . Определение. Ориентированный граф или орграф G , который обозначается G( V , E ) состоит из множества V вершин и множества Eупорядоченных пар элементов из V ., называемого множеством ориентированных ребер или просто ребер . элемент множества E называется ориентированным ребром .Если (a, b) 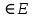 , то a называется начальной вершиной, а b называется конечной вершиной . , то a называется начальной вершиной, а b называется конечной вершиной .Ребро (a, b) называется дугой, соединяющей a иb . Определение. Размеченный граф G=G (V, L,E) представляет собой множество вершин V, множество меток L и множества , которое является подмножеством множества V 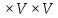 . Таким образом ребро eграфа G имеет вид (a,l,b) , где l–метка , а aи bвершины . . Таким образом ребро eграфа G имеет вид (a,l,b) , где l–метка , а aи bвершины . Определение.Ориентированный граф  ( (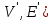 называется ориентированным подграфом ориентированного графа G( V , E ) , если называется ориентированным подграфом ориентированного графа G( V , E ) , если 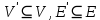 . . Определение. Ориентированный путь из a вb задается последовательностью вершин 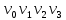 … …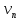 , гдеa= , гдеa=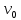 , b= , b=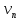 и ( и (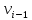 , ,  ) для 1 ) для 1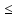 i i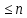 –ориентированные ребра . –ориентированные ребра .Длиной ориентированного пути называется количество ориентированных ребер , входящих в путь . Определение. Если считать ребра ориентированного графаG неориентированными, то такой граф будем называть графом, соотнесенным с графом G . Определение. Ориентированный графG( V , E ) называется связным , если его соотнесенный граф является связным . Ориентированный граф называется сильно связным, если для каждой пары вершин a,b  Vсуществует ориентированный путь из aв b . Vсуществует ориентированный путь из aв b .Определение. Ориентированное дерево Tпредставляет собой свободный от петель ориентированный граф, соотнесенный граф которого является деревом. Если в ориентированном дереве существует ребро (a, b), то не существует ребра (b ,a), так как в этом случае путь abaбыл бы циклом и путь из aв bбыл бы не единственным. Таким образом , если (a, b) 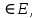 то (b ,a ) то (b ,a )  . Такое отношение называется . Такое отношение называетсяасиметричным . Вершина в самой верхней части изображения дерева называется корнем дерева. Если корень дерева определен , то дерево называется корневым деревом .Если ориентировать корневое дерево , то получится корневое ориентированное дерево 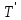 , ,Порожденное корневым деревом . Пусть корень дерева выбран. Уровень вершины vопределяется длиной единственного пути из корня в вершину v. Если рассматривается корневое ориентированное дерево 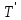 , , Порожденное данным корневым деревом T, тогда вершина uназывается родителем вершины v , а v называется сыном вершины u , если существует ориентированное ребро из u в v. Если u – родитель v и 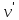 , тогда v и , тогда v и 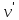 называются братьями . Если существует ориентированный путь из вершины u в вершину v , тогда u называется предком называются братьями . Если существует ориентированный путь из вершины u в вершину v , тогда u называется предкомвершины v , а v называется потомком вершины u . Если наибольшая из степеней выхода для вершины дерева равна m, то дерево называется m- арным деревом . При m=2 – бинарное дерево . Определяется левый и правый сын в каждом бинарном дереве . Определение. Пусть G=G (V , E ) – ориентированный граф . Ориентированным циклом называется ориентированный путь ненулевой длины из вершины в ту же вершину без повторения ребер . Определение. Пусть G=G (V , E ) – ориентированный граф. Ориентированный цикл , который включает все ребра и вершины графа G , называется эйлеровым циклом . В этом случае говорят , что ориентированный граф G имеет эйлеров цикл . |
