конечные графы. Вершинами графа, элементы множества e называются ребрами графа а пара (V, e ), т е. множество вершин и ребер графа называется графом. Если две вершины графа соединены ребром, то такие вершины называются смежными
 Скачать 350.58 Kb. Скачать 350.58 Kb.
|
|
Теорема . Пусть G –(ориентированный ) граф с вершинами 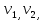 …, …,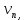 и матрицей смежности А . Путь длины kили k-путь из и матрицей смежности А . Путь длины kили k-путь из  в в 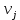 для 1 для 1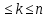 существует тогда и только тогда , когда существует тогда и только тогда , когда 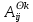 =1. =1.Теорема . Пусть G –(ориентированный ) граф с вершинами 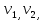 …, …,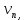 и матрицей смежности А . Из вершины и матрицей смежности А . Из вершины  в вершину в вершину 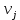 имеется mпутей длины k , где 1 имеется mпутей длины k , где 1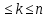 тогда и только тогда , когда 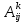 =m , где =m , где 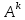 =A =A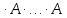 обычное умножение матриц . обычное умножение матриц . = = Теорема . Пусть G –(ориентированный ) граф с вершинами 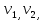 …, …,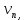 и матрицей смежности А . Пусть и матрицей смежности А . Пусть 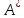 =AV =AV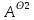 V V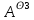 V… V V… V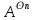 . Тогда . Тогда 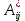 =1 тогда и только тогда , когда существует путь из =1 тогда и только тогда , когда существует путь из  в в 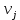 . .Теорема . Пусть G –(ориентированный ) граф с вершинами 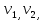 …, …,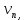 и матрицей смежности А. Пусть и матрицей смежности А. Пусть 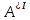 =IVAV =IVAV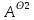 V V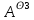 V… V V… V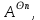 где I единичная матрица . Тогда где I единичная матрица . Тогда 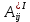 =1 для всех Iи jтогда и только тогда , когда граф G(сильно ) связный . =1 для всех Iи jтогда и только тогда , когда граф G(сильно ) связный .Найдите матрицы а) инцидентности , б) матрицы смежности следующих графов :   • •   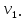  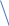  • •  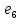 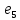   • •              • •  3. • 3. • 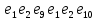 •         • •  • •  •   • •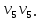 • • 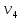 4    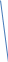   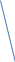    . . • • • •  • • 5. • 5. • • •  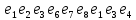 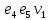  • •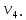 • •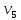 • •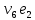 •  • •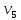 6         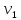 • • 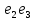 • • 7. • 7. •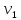 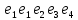 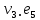    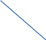  • •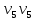 • • 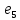 • • 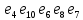 •  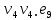 • • 8.Для заданной матрицы инцидентности найдите соответствующий граф .  9.Для заданной матрицы смежности найдите соответствующий граф . 1) 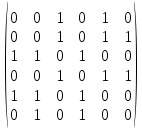 2) 2)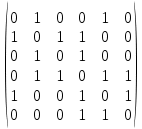 10.Для заданных графов а) найдите матрицы смежности .б) Используя матрицу смежности , найдите все пути длины 2 .в) Используя матрицу смежности , найдите все пути длины 3 .        • • • • 2) d• •f 2) d• •f   b• •e b• •e • • • • • • a• •c 3     )e• 4) • )e• 4) • c       • •d • •d • • • •   •b •b • •  •a •a • •  • • 11. Используя тот факт , что  =AV =AV V V V… V V… V , определите транзитивное замыкание отношения , представленного графом , определите транзитивное замыкание отношения , представленного графом1   ) )     • • • • 2) •e 2) •e      c• •d c• •d•b  • • • • • • •a •a    •b 4) • •b 4) •       a• •c a• •c  • •  •d • •d • • • |
