7 класс геометрия. Вертикальные углы (определение ). Свойство вертикальных углов
 Скачать 91.08 Kb. Скачать 91.08 Kb.
|
|
Билет 1. Вертикальные углы (определение ).Свойство вертикальных углов. 2.Признаки равенства треугольников (3 пр.) 3.Виды углов образованных при пересечении двух прямых секущей 4. решите задачу. 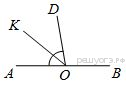 Найдите величину угла DOK, если OK — биссектриса угла AOD, Найдите величину угла DOK, если OK — биссектриса угла AOD,∠DOB = 108°. Ответ дайте в градусах. 5. Выберите неверное утверждение: 1) Биссектриса равнобедренного треугольника, проведённая из вершины, противолежащей основанию, делит основание на две равные части. 2) Если угол острый, то смежный с ним угол также является острым. 3) Для точки, лежащей на окружности, расстояние до центра окружности равно радиусу Билет 2. 1.Смежные углы (определение). Свойство смежных углов. 2. Параллельные прямые (определение и признаки) 3. Стороны прямоугольного треугольника (гипотенуза и катет) 4 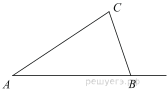 .Решите задачу: .Решите задачу:В треугольнике АВС угол А равен 40  , внешний угол при вершине В , внешний угол при вершине В равен 102  Найдите угол С. Ответ дайте в градусах. Найдите угол С. Ответ дайте в градусах.5.Выберите верное утверждение: 1) Через точку, не лежащую на данной прямой, можно провести прямую, параллельную этой прямой. 2) Треугольник со сторонами 1, 2, 4 существует. 3). Любая высота равнобедренного треугольника является его биссектрисой. Билет 3. 1. Перпендикулярные прямые (определение) 2.Свойства параллельных прямых 3. Периметр треугольника 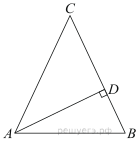 4.Решите задачу В треугольнике ABC AC = BC, AD — высота, угол BAD равен 24°. Найдите угол C. Ответ дайте в градусах. 5. Выберите верное утверждение: 1) Если два угла и сторона одного треугольника равны двум углам и стороне другого треугольника, то такие треугольники равны. 2) Вертикальные углы равны. 3) Любая биссектриса равнобедренного треугольника является его медианой Билет 4. 1.Середина отрезка (определение) 2.Признаки равенства прямоугольных треугольников 3. Внешний угол 4 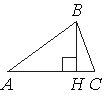 .Решите задачу: .Решите задачу:В остроугольном треугольнике ABC проведена высота BH, ∠BAC=37°. Найдите угол ABH. Ответ дайте в градусах 5. Выберите верное утверждение: 1) Если два угла и сторона одного треугольника равны двум углам и стороне другого треугольника, то такие треугольники равны. 2) Вертикальные углы равны. 3) Любая биссектриса равнобедренного треугольника является его медианой. Билет 5. 1.Определение равных треугольников 2. Медианы, биссектрисы, высоты треугольника (определение и изображение на рисунке) 3.Сумма углов треугольника. 4 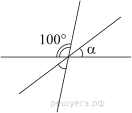 .Решите задачу: .Решите задачу:Углы, отмеченные на рисунке одной дугой, равны. Найдите угол 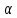 . . Ответ дайте в градусах 5. Выберите верное утверждение: 1) Через точку, не лежащую на данной прямой, можно провести прямую, параллельную этой прямой. 2) Треугольник со сторонами 1, 2, 4 существует. 3). Любая высота равнобедренного треугольника является его биссектрисой. Билет 6. 1.Определение равнобедренного треугольника 2.Окружность и ее элементы (определения, показать на рисунке) 3.Неравенство треугольника 4.Решите задачу: Н 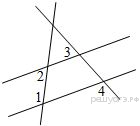 а плоскости даны четыре прямые. Известно, что а плоскости даны четыре прямые. Известно, что Ответ дайте в градусах. 5. Выберите верное утверждение: 1) Если два угла и сторона одного треугольника равны двум углам и стороне другого треугольника, то такие треугольники равны. 2) Вертикальные углы равны. 3) Любая биссектриса равнобедренного треугольника является его медианой. Билет 7. 1.Виды треугольников 2.Свойства прямоугольного треугольника 3.Аксиома параллельных прямых и ее следствия 4. решите задачу: Н  айдите величину угла DOK, если OK — биссектриса айдите величину угла DOK, если OK — биссектриса угла AOD, ∠DOB = 108°. Ответ дайте в градусах. 5. Выберите неверное утверждение: 1) Биссектриса равнобедренного треугольника, проведённая из вершины, противолежащей основанию, делит основание на две равные части. 2) Если угол острый, то смежный с ним угол также является острым. 3) Для точки, лежащей на окружности, расстояние до центра окружности равно радиусу Билет 8. 1. Окружность и ее элементы (показать на рисунке) 2.Признаки равенства прямоугольных треугольников 3.Свойства равнобедренного треугольника 4 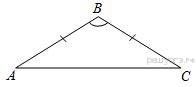 .Решите задачу: .Решите задачу:В треугольнике Найдите угол 5. Выберите неверное утверждение: 1) Если угол равен 45°, то вертикальный с ним угол равен 45°. 2) Любые две прямые имеют ровно одну общую точку. 3) Через любые три точки проходит ровно одна прямая Билет 9. 1.Соотношение между сторонами и углами треугольника 2.Свойства прямоугольного треугольника 3. Смежные углы (определение и св-ва) 4 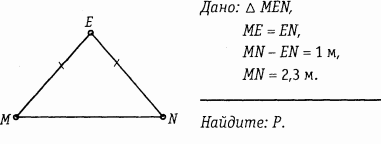 .Решите задачу: .Решите задачу:Дано: 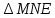 -равнобедренный, -равнобедренный, MN= 1см , MЕ = 2,3 см Найти: Р треугольника 5. Выберите неверное утверждение: 1) Каждая сторона треугольника меньше разности двух других сторон. 2) В равнобедренном треугольнике имеется не более двух равных углов. 3) Если три стороны одного треугольника соответственно равны трем сторонам другого треугольника, то такие треугольники равны |
