7б свойства пр треуг и признаки рав прямоуг треуг. Свойства прямоугольных треугольников. Признаки равенства прямоугольных треугольников

• Название: Свойства прямоугольных треугольников. Признаки равенства прямоугольных треугольников
• Анкор: 7б свойства пр треуг и признаки рав прямоуг треуг
• Дата: 11.04.2022
• Размер: 388.5 Kb.
• Имя файла: 7б свойства пр треуг и признаки рав прямоуг треуг.doc
• Тип: Урок; #462407

Открытый урок геометрии в 7-ом классе на

районном семинаре

на тему:

«Свойства прямоугольных треугольников. Признаки равенства прямоугольных треугольников»

.


Тема: Решение задач по теме «Свойства прямоугольных треугольников. Признаки равенства прямоугольных треугольников.

Тип урока: Урок когнитивного типа. Урок обобщения знаний по теме.

Форма урока: Урок исследование, постановки проблемы и ее решения.

Учебно-методическое обеспечение: Л.С. Анастасян «Геометрия 7 – 9 кл.»

Время реализации: 40 мин.

Компьютерные медиапродукты. Наглядная презентация учебного материала, сделанная в среде Power Point.

Данный медиапродукт построен непосредственно на сопровождении сценария урока и содержит необходимые иллюстрации для объяснения материала.

Цель урока: применение теоретических знаний на практике, умение переносить их и пользоваться ими в нестандартной ситуации.

Задачи урока:

• 
  Образовательные – обобщение теоретических знаний учащихся по теме «Прямоугольные треугольники», показать практическое применение свойств и признаков равенства прямоугольных треугольников;
  
• 
  Развивающие – развитие умений сравнивать, анализировать, обобщать, делать выводы; формировать исследовательскую культуру; развивать интерес к знаниям; переносить теоретические знания на практику;
  
• 
  Воспитательные – формирование умений работать в группах; принимать совместные решения; уверенности в своих силах.
  

Необходимое оборудование и материалы для занятия: компьютер, проектор, экран, табель – календари различных лет, карточки для практического задания, карточки для доказательства задачи, треугольники для работы в группах.

План урока:

Этапы занятия	Временная реализация
I. Организационный момент: приветствие, объявление темы урока.	2
II. Актуализация опорных знаний учащихся: фронтальный опрос по теории, решение задач на готовых чертежах.	7
III. Создание проблемной ситуации. Выдвижение гипотез. Проверка гипотез при помощи измерений. Работа в группах. Обсуждение гипотез.	10
IV. Формулировка и доказательство задачи. Проверка гипотезы при помощи доказательства.	8
V. Совместная работа учителя и учащихся над проблемными вопросами учителя.	10
VI. Домашнее задание.	1
VII. Рефлексия урока.	2

Учить не мыслям, а мыслить.

Кант

Сценарий урока.
I этап: Организационный момент: Приветствие, сообщение порядка работы, выбор лидера групп.

Учитель: Ребята, на прошлом уроке мы решали задачи по теме «Прямоугольные треугольники». Сегодня я вам предложу еще одну задачу на эту тему. Вы обратили внимание на то, что у вас на столе лежат табель-календарики. Задача, которую я вам предложу сегодня для исследования будет связана с календарем. Геометрия в календаре! Необычно? Сегодня у нас много будет необычного. Но это впереди, а пока мы повторим пройденный материал.
II этап: Актуализация опорных знаний учащихся. (По ходу урока идет просмотр презентации)

1. Фронтальный опрос. (слайд №3). Повторение теоретических знаний.

• 
  Какой треугольник называется прямоугольным? Как называются его стороны?
  
• 
  Какие признаки равенства прямоугольных треугольников вы знаете?
  
• 
  Перечистлите свойства прямоугольных треугольников.
  

2. Решение задач по готовым чертежам с целью повторения свойств прямоугольного треугольника и признаков равенства прямоугольных треугольников. (Рисунки к задачам готовятся заранее на планшетах.) . (Слайды № 4, 5).

1). Устно. Определить вид треугольника. ( ∆АВС – прямоугольный.)



Какое свойство прямоугольного треугольника это подтверждает?

На ваших партах красные треугольники

Проверим это свойство практически. Свернем у красных прямоугольных треугольников острые углы к прямому (если есть затруднения показать, как это сделать).

Сделайте вывод (В прямоугольном треугольнике сумма острых углов равна 90°).

2). Устно. Докажите, что треугольники АВС и NKM равны.




(В=35°; N=55°. Против равных углов лежат равные стороны. Значит, СВ=КМ, АС=МК. ∆АВС= ∆NKM по двум катетам.)

3). Письменно у доски. Определить вид треугольника ВМС (данная задача готовит учащихся к доказательству проблемной задачи в календаре).


Решение.

1=55°, 2=35°, против равных углов лежат равные стороны, значит

АВ = МD, АМ = СD.

∆АВМ=∆МСD (по двум катетам), следовательно ВМ=МС, ∆ВМС – равнобедренный.
Учитель: Докажите, что ∆ВМС – прямоугольный.

Углы 1 и 2 дополняют угол 3 до развернутого. 1+2+3=180°. 1+2=90°, следовательно 3=90°. ∆ВМС – прямоугольный.

Вывод: ∆ВМС – равнобедренный прямоугольный.
III этап. Создание проблемной ситуации. Выдвижение гипотез. Проверка гипотез.

1. Учитель: Ребята, у вас на столе лежат табель–календари за 2021 г. Соедините в апреле этого года числа 10, 20, 30. Какую фигуру получили? (Треугольник). Чтобы в дальнейшем было легче работать с календарем, сделали его на клетчатой бумаге. Возьмите такой календарь за декабрь 2020 г. и соедините центры клеток с числами 10, 20, 30. Получили треугольник. (слайд № 7.) Назовите его (10–20–30). Необычно? Да. Но сегодня будем обозначать треугольники, отрезки и углы числами. Назовите стороны треугольника и его углы.

Как вы думаете, какой получился треугольник? Нам предстоит сейчас решить эту проблему. (слайд № 7)

2. Выдвижение гипотезы учащимися: (слайд № 8.)

а) равнобедренный;

б) прямоугольный;

в) равнобедренный прямоугольный.
Учитель: Для того, чтобы доказать или опровергнуть вашу гипотезу у вас имеются чертежные прямоугольные треугольники, линейка и вырезанный треугольник 10–20–30. В группах обсудите, как, используя эти инструменты, определить вид треугольника 10–20–30.

3. Работа в группах. (учащиеся при помощи измерений определяют вид треугольника. У каждой группы имеются необходимые инструменты для каждого ученика).

4. Обсуждение гипотез. Разбираются представленные гипотезы. Один человек от группы презентует классу свое решение.

4.1. Измерили линейкой и треугольником стороны и угол 10 . Получили равнобедренный прямоугольный треугольник 10–20–30 с прямым углом 10.

4.2. Измерили углы в данном треугольнике. Они равны 45°, 45°, 90°. Треугольник 10–20–30 – прямоугольный. Так как углы при основании равны, то он еще и равнобедренный.

4.3. Угол 10 – прямой. Проверили чертежным треугольником Свернем острые углы к углу 10. Сумма острых углов в треугольнике равна прямому т.е. 90°. Это свойство прямоугольных треугольников.

Треугольник 10–20–30 – равнобедренный прямоугольный.

Вывод: Треугольник 10–20–30 – равнобедренный прямоугольный.

(слайд № 9.)

IV этап. Формулировка и доказательство задачи. (Проверка гипотезы при помощи доказательства).

Учитель: Вид треугольника мы определили при помощи измерений. Мы уже говорили с вами, что измерениям доверять нельзя из-за возможных погрешностей. Любые экспериментальные данные в геометрии требуют доказательства.

Давайте сформулируем задачу, которую нам надо решить.

Задача.

(слайд № 10)

5. Совместная работа учителя и обучающихся. (Учащиеся работают с карточками декабря 2020 г, сделанными на клетчатой бумаге, где имеется доказательство с пропусками) (приложение 1).

Доказательство. (слайд № 11).

Учитель: Соединим центры клеток, соответствующих чисел. Сделаем дополнительные построения: проведем отрезки 30 – 9,

9 –13 и 13–20. Получили два треугольника: 30–9–10 и 10–13–20. Докажите, что:

а). треугольники 30–9–10 и 10–13–20 равны;

б). стороны 10–30 и 10–20 равны.

(Углы 9 и 13 прямые, стороны 9–30 и 10–13 равны соответственно сторонам 13–20 и 10–13. Значит, треугольники равны по двум катетам. Так как треугольники равны, то равны и их гипотенузы. Стороны 30–10 и 10–20 равны.)

Учитель: Определите вид треугольника 10–20–30 (равнобедренный).

Докажите, что угол 30–10–20 – прямой.

(Из равенства треугольников 30–9–10 и 10–13–20 следует, что углы 9–30–10 и 20–13–10 равны углам 30–9–10 и 10–13–20 соответственно. В прямоугольном треугольнике сумма острых углов 9–10–30 и 13–10–20 равна 90°. Углы 9–10–30 и 13–10–20 дополняют угол 30–10–20 до развернутого, значит угол 30 –10–20 равен 180–90=90°.)

Вывод: треугольник 10–20–30 – равнобедренный прямоугольный.

(слайд № 12)
V этап. Совместная работа учителя и учащихся над проблемными вопросами учителя.

Учитель: Ребята, как вы думаете, такой результат будет только для декабря 2020 г.? А верно ли это утверждение для декабря любого года? (да).

Давайте проверим вашу гипотезу.

1. Работа в группах. (учащиеся работают с табель–календарями, соединяют центры клеток чисел 10–20–30 в декабрях различных лет). (приложение 2).

2. Обсуждение результатов. (рисунки вывешены на доске). (слайды № 13-15).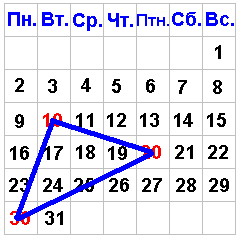



2006 2007 2008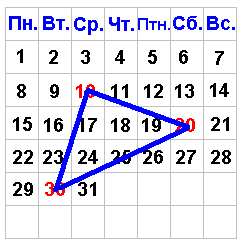


2003 2009 2010

Вопросы учителя:

• 
  Проанализируйте рисунки. Какой вывод вы можете сделать? (получаются 6 прямоугольных равнобедренных треугольников и отрезок);
  
• 
  Отчего зависит расположение треугольников? (от расположения чисел в декабре месяце);
  
• 
  Сколько существует различных вариантов расположения дат в декабрьском календаре. (Семь. Это зависит оттого, каким днем недели будет 1 декабря);
  
• 
  Когда получается отрезок? (когда центры клеток чисел 10, 20, 30 лежат на одной прямой);
  
• 
  Сколько различных треугольников получилось? (два: с прямым углом 10 и прямым углом 30).
  

VI этап. Домашнее задание.

Для ситуации, когда прямым углом является угол 10, мы провели доказательство. По образцу классной работы докажите дома, что и во втором случае (угол 30 прямой) получится равнобедренный прямоугольный треугольник. Рассуждения будут аналогичными

VII этап. Рефлексия урока.

Учитель:

• 
  Какие знания помогли вам исследовать такую нестандартную задачу? (Свойства и признаки прямоугольных треугольников; свойства развернутого угла; свойства треугольника; умение измерять углы).
  
• 
  Проанализируйте свою работу на уроке. Оцените свою работу
  

• 
  Поднимите руки те, кому было на уроке трудно, но интересно?
  
• 
  Поднимите руки те, кому было на уроке понятно, но остались вопросы?
  
• 
  Поднимите руки те, кому было все понятно.
  

Сегодня на уроке вы увидели необычное в привычном. Вы замечательно работали! Всем спасибо за урок!

Приложение 1

Задача. Доказать, что при соединении чисел 10, 20, 30 в декабре 2020 г. получится равнобедренный прямоугольный треугольник.


Доказательство

Проведем отрезки 30–9, 9–13 и 13–20. Получили два треугольника 30–9–10 и ________. Углы 9 и __ прямые. Отрезки 9–10 и _____ равны. Отрезки ______ и 13-20 равны. Треугольники ______ и ______ равны по ___________________.

Из равенства треугольников 30–9–10 и 13–20–10 следует, что равны и гипотенузы _____ и _____. Треугольник 10–20–30 – равнобедренный.

Из равенства треугольников 30–9–10 и 13–20–10 следует, что углы 9–10–30 и 13–20–10; 9–10–30 и 13–20–10 равны (лежат против равных сторон). Углы ___ и ___ дополняют угол 30–10–20 до развернутого.

Сумма углов 9–10–30 и 13–10–20 равна 90° по свойству прямоугольного треугольника.

Значит, угол 30–10–20 равен 180° – ___ = ___, то есть треугольник 10–20–30 – ____________________.

Вывод: треугольник 10–20–30 – равнобедренный, прямоугольный.

Приложение 2

Календарь декабрей разных лет.