ОПД. Выбор профессии один из серьезнейших шагов молодежи
 Скачать 1.37 Mb. Скачать 1.37 Mb.
|
|
СОДЕРЖАНИЕ: ВВЕДЕНИЕ Выбор профессии – один из серьезнейших шагов молодежи. Оттого насколько адекватно он совершен, отвечает ли выбранная профессия способностям, интересам и склонностям, востребованности на рынке труда зависит многое в дальнейшей жизни молодого человека. Важно знать и чисто бытовые особенности профессиональной жизни: каков характер рабочего дня, с какой техникой придется иметь дело, с какими людьми общаться, в какое время года обычно отпуск, какова зарплата и др. Профессии электрика существуют практически во всех отраслях производства начиная с добычи энергоресурсов, их переработке, получения и использования электроэнергии. Любая профессия топливно-энергетического комплекса позволяет человеку побывать в разных уголках не только родной страны. Это связанно с разными климатическими и погодными условиями для чего необходим достаточный уровень здоровья. Работа в электроэнергетике по любой специальности и на любой должности отличается напряженными разъездами и ненормированным характером в отношении рабочего времени. Это связанно с масштабами электроэнергетической системы (предприятие, поселок, город, регион). При этом специалист может заниматься монтажом, наладкой, контролем и ремонтом электротехнического оборудования в любую погоду, зачастую вдали от какого - либо населенного пункта. Профессии и специальности в электроэнергетическом комплексе достаточно разнообразны. Получив любую из них, выпускник должен отчетливо представлять, что:
Характер и содержание работы:
Необходимо отметить, что везде к дисциплине работника в электроэнергетике предъявляются требования сродни армейским, т.к. объекты электроэнергетики не только в ряде случаев повышенной опасности для населения, но и являются объектами жизнеобеспечения всей инфраструктуры городов, производственных предприятий, объектов сельского хозяйства. ГЛАВА 1 ОСНОВНЫЕ ЗАКОНЫ ЭЛЕКТРОТЕХНИКИ 1.1. ЭЛЕКТРИЧЕСКОЕ ПОЛЕ, ЕГО СИЛОВЫЕ И ЭНЕРГЕТИЧЕСИКЕ ХАРАКТЕРИСТИКИ Заряженные тела взаимодействуют между собой: одноименно заряженные - отталкиваются, разноименно заряженные – притягиваются. Это взаимодействие происходит на расстоянии и передается не мгновенно, а через конечный промежуток времени, т.е. существует конечная скорость передачи взаимодействия. Объяснение действия на расстоянии вызвало много гипотез, в результате которых возникла теория близкодействия, центральным понятием которой является понятие силового поля. Заряженное тело является источником электрического поля. Взаимодействие заряженных тел объясняется тем, что каждое из них создает в окружающем пространстве поле, которое действует на другое заряженное тело с некоторой силой. Электрическое поле является одной из форм материи, оно столь же реально, как и обычное вещество. Поле обладает энергией. Согласно закону Эйнштейна энергия 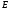 связанна с массой связанна с массой 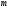 зависимостью зависимостью 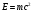 , где , где 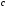 - скорость света, поэтому поле должно иметь и массу. - скорость света, поэтому поле должно иметь и массу.Электрическое поле – одна из двух сторон электромагнитного поля, характеризующаяся воздействием на электрически заряженную частицу с силой, пропорционально заряду частицы и не зависящей от ее скорости. Строго говоря, в природе отдельно не существуют электрическое и магнитное поля, они являются проявлением единого электромагнитного поля. Отдельно рассматривать электрическое поле можно лишь в том случае, если магнитное поле достаточно мало и его влияние на изучаемые процессы не существенно. В аналогичной ситуации рассматривается и магнитное поле. Взаимодействие заряженных тел зависит от их формы. Чтобы устранить влияние формы тела и установить общие закономерности сил, действующих на заряды в электрическом поле, рассматривают так называемые точечные заряды, т.е. такие заряженные тела, размеры которых намного меньше расстояния между ними. Сила 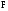 взаимодействия двух точечных зарядов взаимодействия двух точечных зарядов 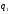 и и 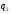 определяется законом Кулона определяется законом Кулона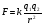 . .Эта сила пропорциональна произведению величин зарядов и обратно пропорциональна квадрату расстояния  между ними. между ними.Электрическая сила взаимодействия двух зарядов зависит от расстояния так же, как и сила тяготения. Ее отличие от силы тяготения состоит, во-первых, в изменении знака силы в зависимости от знака заряда (сила может быть отталкивающей и притягивающей), а, во-вторых, в том, что эта сила неизмеримо больше силы тяготения (в 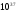 раз!). раз!).Важнейшей характеристикой электрического поля, определяющей его действие на неподвижный заряд, является напряженность. Если величина и линейные размеры заряда достаточно малы и практически не искажают исследуемое поле, то для различных по величине зарядов отношение силы, действующей на заряд, к его величине, т.е. 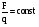 . Следовательно, это отношение не зависит от величины заряда, а определяется только полем в данной точке. . Следовательно, это отношение не зависит от величины заряда, а определяется только полем в данной точке.Отношение 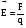 является векторной характеристикой электрического поля и называется напряженностью поля. Она равна силе, действующей на единичный положительный заряд, помещенный в данную точку поля. Графически электрическое поле изображают линиями напряженности, называемыми также электрическими силовыми линиями. Электрическое поле уединенного заряда представляется в виде силовых линий, имеющих вид лучей, выходящих из центра, где расположен заряд (рис. 1.1, а). Поле в точке 2, созданное зарядом 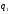 , расположенным в точке 1: , расположенным в точке 1: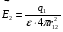 , ,где 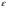 - диэлектрическая проницаемость среды. - диэлектрическая проницаемость среды.Электрическое поле двух одноименных и двух разноименных зарядов показано на рис. 1.1, б, в. Поле может создаваться множеством источников и не обязательно определяется путем сложения полей отдельных зарядов, а может быть определенно по распределению плотности поверхностного или объемного заряда. Если поле 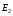 каким-то образом измерено или рассчитано в месте расположения заряда каким-то образом измерено или рассчитано в месте расположения заряда 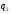 , то сила, действующая на заряд , то сила, действующая на заряд 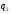 , ,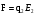 . .Электрическое поле может иметь сложную форму, например в высоковольтном изоляторе. Поле в плоском конденсаторе равномерно, за исключением краев (рис. 1.1, г). 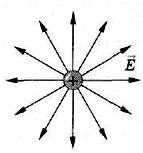 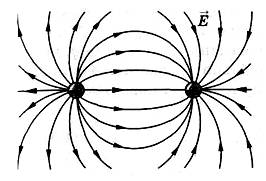 а б 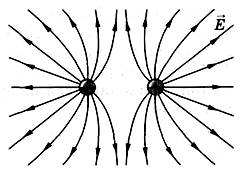 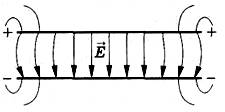 в г Рис.1.1. Конфигурация электрический полей: а – уединенного положительно заряда; б – двух разноименных зарядов; в – двух одноименных зарядов; г – плоского конденсатора. Линии электростатического поля начинаются на положительном заряде и оканчиваются на отрицательном, т.е. они не замкнуты. Незамкнутые силовые линии означают наличие источников поля - зарядов. Заряженное тело, например проводник, изолированный от земли, обладает потенциалом относительно земли. Потенциал 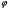 в данной точке измеряемся работой, которую необходимо затратить, чтобы перенести единицу заряда из бесконечности в данную точку. В бесконечности, под которой можно понимать землю, потенциал принимается равным нулю. В отличие от напряженности, являющейся векторной величиной, потенциал – величина скалярная. Он является энергетической характеристикой поля и определяет потенциальную энергию заряда в данной точке измеряемся работой, которую необходимо затратить, чтобы перенести единицу заряда из бесконечности в данную точку. В бесконечности, под которой можно понимать землю, потенциал принимается равным нулю. В отличие от напряженности, являющейся векторной величиной, потенциал – величина скалярная. Он является энергетической характеристикой поля и определяет потенциальную энергию заряда 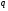 в данной точке поля: в данной точке поля: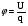 . .Потенциальная энергия 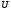 определена с точностью до произвольной постоянной, это же относится и к потенциалу определена с точностью до произвольной постоянной, это же относится и к потенциалу 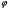 . Поэтому практический интерес представляют не сами потенциалы точек поля, а их разность или изменение потенциала при перемещении из одной точки поля в другую. Разность потенциалов между двумя точками равна напряжению . Поэтому практический интерес представляют не сами потенциалы точек поля, а их разность или изменение потенциала при перемещении из одной точки поля в другую. Разность потенциалов между двумя точками равна напряжению 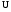 и может быть рассчитана, если известно распределение электрического поля между ними. Для плоского конденсатора, например, считая поле равномерным, получим и может быть рассчитана, если известно распределение электрического поля между ними. Для плоского конденсатора, например, считая поле равномерным, получим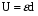 , ,т.е. разность потенциалов равна напряженности электрического поля, умноженной на расстояние  между обкладками. Зная распределение потенциалов в различных точках поля, можно определить его напряженность. Если при перемещении на величину между обкладками. Зная распределение потенциалов в различных точках поля, можно определить его напряженность. Если при перемещении на величину 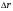 потенциал изменяется на потенциал изменяется на 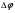 , то проекция вектора напряженности электрического поля на направление перемещения , то проекция вектора напряженности электрического поля на направление перемещения 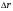 определяется по формуле определяется по формуле 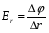 . .Отсюда следует, что напряженность поля определяется изменением потенциала и направлена в сторону его уменьшения. Если разность потенциалов между любыми точками некоторой поверхности равна нулю, то составляющая напряженности поля вдоль такой поверхности также равна нулю и, следовательно, вектор напряженности электрического поля 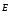 может быть только перпендикулярен, и направлен в сторону наиболее быстрого уменьшения потенциала. может быть только перпендикулярен, и направлен в сторону наиболее быстрого уменьшения потенциала.Важной характеристикой электрического поля является также вектор электрического смещения 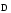 . Он связан с вектором . Он связан с вектором 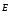 соотношением соотношением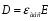 , ,где 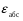 - абсолютная диэлектрическая проницаемость вещества, равная произведению диэлектрической проницаемости вещества - абсолютная диэлектрическая проницаемость вещества, равная произведению диэлектрической проницаемости вещества 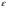 (безразмерная величина) и электрической постоянной (безразмерная величина) и электрической постоянной 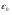 (диэлектрической проницаемости вакуума), т.е. (диэлектрической проницаемости вакуума), т.е.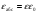 , , причем 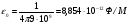 . .Вектор напряженности электрического поля 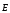 изменяется при переходе из одной среды с диэлектрической проницаемостью изменяется при переходе из одной среды с диэлектрической проницаемостью 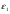 в другую среду с диэлектрической проницаемостью в другую среду с диэлектрической проницаемостью 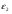 , а вектор , а вектор 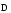 остается неизменным. остается неизменным.У поверхности проводника при отсутствии пространственных свободных зарядов в прилегающих слоях диэлектрика величина вектора электрического смещения равна поверхностной плотности заряда 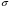 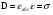 . .При равномерном распределении заряда 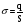 или или 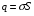 , ,где 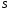 - площадь поверхности проводника. - площадь поверхности проводника.Одной из важнейших физических характеристик проводников является их электрическая емкость. Если к уединенному проводнику (т.е. проводнику, вблизи которого нет других тел, влияющих на распределение зарядов на нем) подвести заряд 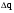 , то потенциал возрастет на величину , то потенциал возрастет на величину 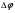 , пропорциональную приращению заряда. Отношение , пропорциональную приращению заряда. Отношение 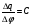 называется электрической емкостью. Емкость проводника характеризует его способность накапливать электрический заряд. Единицей емкости в единицах СИ является фарад (Ф). Это емкость такого проводника, увеличение заряда которого на 1 Кл приводит к повышению его потенциала на 1 В. Фарад очень крупная единица (например, емкость земного шара составляет всего 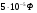 ), поэтому на практике применяются более мелкие единицы: микрофарад ( ), поэтому на практике применяются более мелкие единицы: микрофарад (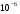 Ф) и пикофарад ( Ф) и пикофарад (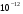 Ф). Значение емкости зависит от размеров тела и расстояния от поверхностей, где сосредоточенны положительные и отрицательные заряды. Ф). Значение емкости зависит от размеров тела и расстояния от поверхностей, где сосредоточенны положительные и отрицательные заряды.Свойство емкости используется в технике для накопления зарядов, т.е. создания накопителей энергии. Такие устройства называются конденсаторами. Конденсатор состоит из проводящих поверхностей, разделенных диэлектриком. Емкость плоского конденсатора 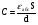 , ,где 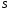 - площадь поверхности одной из обкладок, м2; - площадь поверхности одной из обкладок, м2; 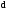 - расстояние между обкладками, м; - расстояние между обкладками, м; 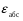 - абсолютная диэлектрическая проницаемость вещества, разделяющая обкладки. - абсолютная диэлектрическая проницаемость вещества, разделяющая обкладки.1.2 МАГНИТНОЕ ПОЛЕ ПОСТОЯННОГО ТОКА Наиболее распространенным видом электрического тока является ток проводимости, представляющий собой направленное движение свободных носителей электрического заряда в веществе или вакууме. Ток создает магнитное поле. Например, ток, протекающий по прямолинейному уединенному проводнику достаточно большой длины, создает магнитное поле, силовые линии которого имеют вид концентрических окружностей. Вектор напряженности магнитного поля в данной точке совпадает с направление касательной к окружности, определяемым по правилу буравчика. Величина напряженности определяется законом полного тока: падение магнитного потенциала вдоль некоторого замкнутого контура, охватывающего ток, равно полному току через этот контур. Полный ток представляет собой алгебраическую сумму всех токов, охваченных контуром. 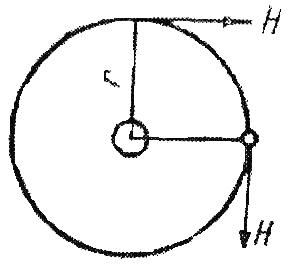 Рис. 1.2 магнитное поле уединенного проводника с током Математически закон полного тока записывается так: 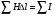 . .Для уединенного прямолинейного проводника с током 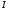 (рис. 1.2) поле на расстоянии (рис. 1.2) поле на расстоянии  одинаково. Тогда на основании закона полного тока одинаково. Тогда на основании закона полного тока 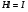 , но так как , но так как 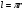 , то , то 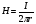 . .Поле двух параллельных прямолинейных проводников с токами может быть получено путем геометрического сложения полей уединенных проводников с токами. 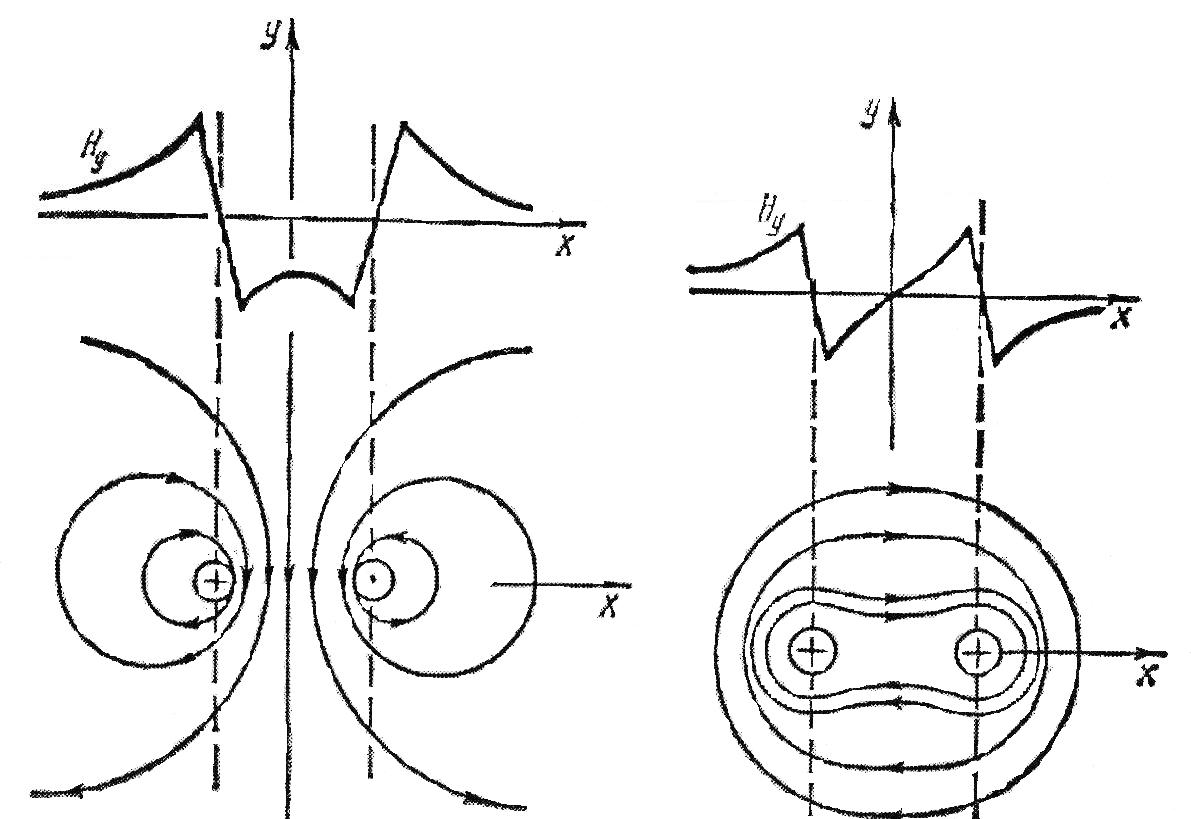 а б Рис. 1.3. магнитное поле параллельных проводников с токами: а – одинакового направления; б – разного. Результирующее поле двух проводников с токами одинакового направления предоставлено на рис. 1.3, а, для токов разного направления – на рис. 1.3, б. На этих же рисунках показано изменение составляющих поля 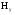 вдоль оси вдоль оси 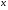 . .При сложении ряда круговых токов образуется поле соленоида (рис. 1.4). Она похоже на поле прямолинейного магнита. Для соленоида достаточно большой длины 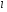 по сравнению с его диаметром поле в центре (без учета влияния концов) по сравнению с его диаметром поле в центре (без учета влияния концов)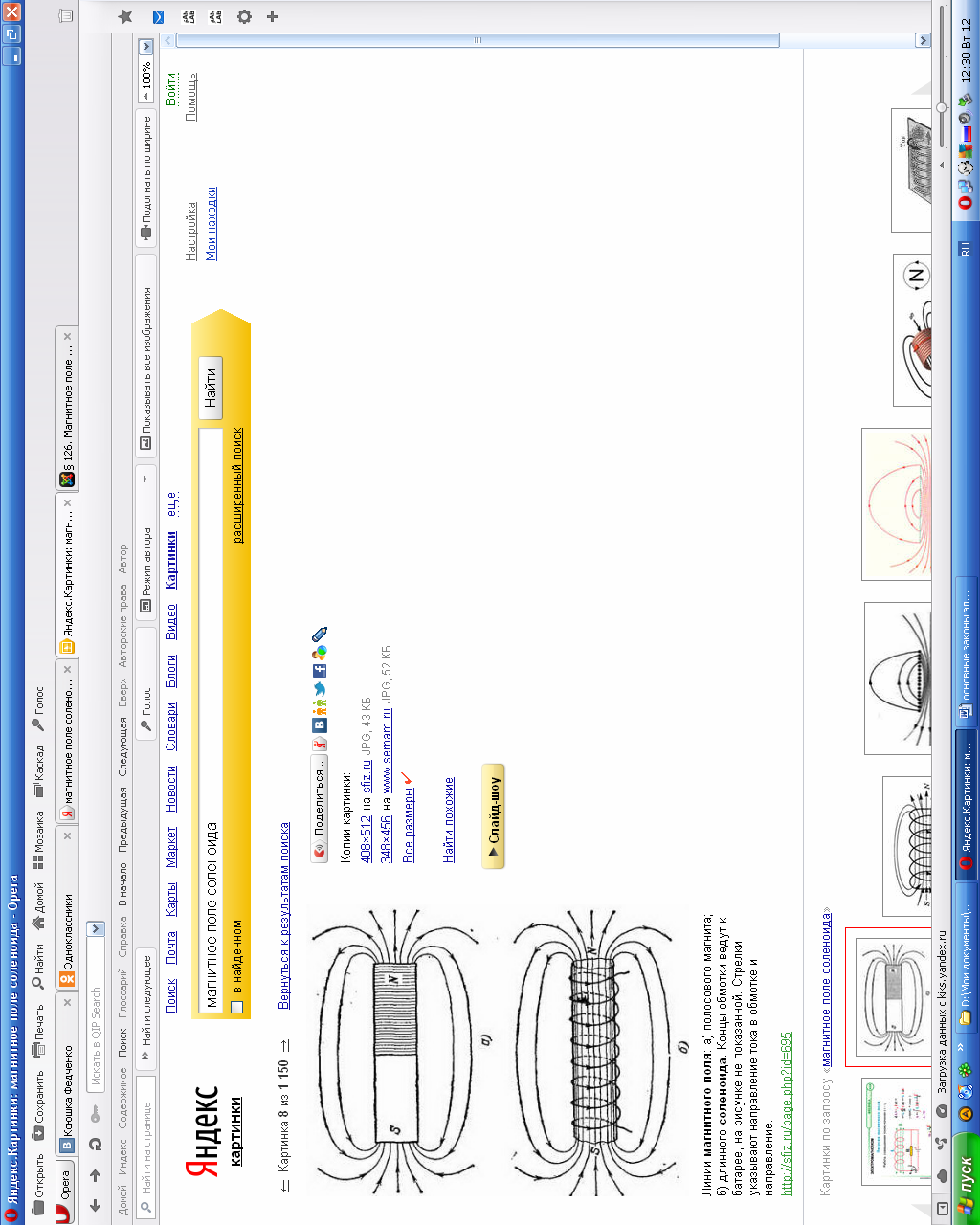 Рис.1.4 магнитное поле соленоида 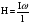 , ,где 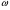 - число витков соленоида. - число витков соленоида.Для любого тока в однородной среде поле может быть рассчитано по закону Био-Савара – Лапласа. Согласно этому закону каждый элемент тока 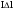 создает на расстоянии создает на расстоянии  от элемента поле от элемента поле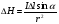 , ,где 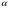 - угол между направлением тока и вектора - угол между направлением тока и вектора 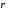 . .Результирующее поле находится суммированием полей отдельных элементов тока. Вектор электромагнитной индукции 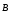 связан с вектором связан с вектором 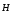 уравнением уравнением 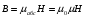 , ,где 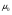 - магнитная постоянная (магнитная проницаемость вакуума); - магнитная постоянная (магнитная проницаемость вакуума); 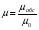 , ,причем 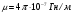 . .Сила взаимодействия между однородным полем индукции 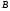 и прямолинейным проводником с током определяется по закону Ампера и прямолинейным проводником с током определяется по закону Ампера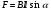 , ,где 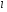 - длина проводника; - длина проводника; 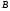 - индукция, постоянная по всей длине - индукция, постоянная по всей длине 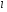 ; ; 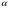 - угол между вектором - угол между вектором 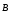 и направлением тока и направлением тока 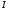 . .Направление силы определяется правилом «левой руки». Однако проще воспользоваться правилом Миткевича, объяснение которого дано в следующем параграфе. Максимальная сила получается, когда 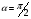 , т.е. когда индукция направлена перпендикулярно току. , т.е. когда индукция направлена перпендикулярно току. Нормальная составляющая вектора 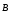 при переходе из одной среды в другую изменяется непрерывно, т.е. при переходе из одной среды в другую изменяется непрерывно, т.е. 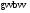 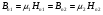 , а нормальная составляющая вектора , а нормальная составляющая вектора 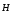 изменяется скачком изменяется скачком 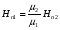 пропорционально отношению магнитных проницаемостей сред пропорционально отношению магнитных проницаемостей сред 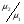 . .Важной особенностью линий магнитного поля является замкнутость магнитных силовых линий. Это указывает на то, что в природе не существует «магнитных» зарядов, являющихся источником поля. Такое поле называется вихревым, в отличие от потенциального поля (электростатического), имеющего источник (заряды). Сравним силы взаимодействия зарядов в электрическом поле и токов в магнитном поле. Силы взаимодействия между зарядами или между полем и помещенным в нем зарядом теоретически могут достигать весьма большой величины. Однако применит эти силы в технике весьма затруднительно по причине возникновения пробоя в диэлектрике. Если пользоваться технически доступными значениями напряженности, например для воздуха 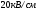 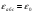 плотность заряда на обкладке плотность заряда на обкладке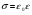 , ,заряд при площади пластин 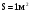 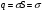 и сила притяжения между пластинами 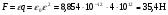 . .Рассчитаем теперь силу взаимодействия двух параллельных проводников с токами. Пусть ток в проводе равен 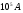 , расстояние между проводами , расстояние между проводами 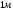 . Тогда по закону Ампера при . Тогда по закону Ампера при 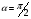 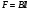 . .Индукция, создаваемая током одного провода в центре другого 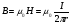 , , Следовательно, при 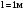 сила сила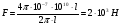 . .Из этого примера становится ясным целесообразность применения магнитного поля как источника электромагнитной силы. 1.3. ЭЛЕКТРОДИНАМИКА. ЭЛЕКТРОМАГНИТНОЕ ПОЛЕ До сих пор мы рассматривали электростатические и магнитостатические поля. Открытия Фарадея, Максвелла, Герца положили начало учению об электромагнитном поле. Закон электромагнитной индукции для проводника длиной 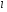 в формулировке Фарадея записывается в виде в формулировке Фарадея записывается в виде 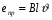 , ,где 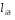 - электродвижущая сила (э.д.с) в проводнике; - электродвижущая сила (э.д.с) в проводнике; 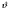 - скорость движения проводника относительно поля; - скорость движения проводника относительно поля; 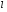 - длина проводника. Если, как показано на рис. 1.5, между полюсами движется проводник и пересекает перпендикулярно направление поля вектора - длина проводника. Если, как показано на рис. 1.5, между полюсами движется проводник и пересекает перпендикулярно направление поля вектора 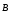 , то в проводнике возникает э.д.с и по замкнутому проводнику пойдет ток в направлении э.д.с. , то в проводнике возникает э.д.с и по замкнутому проводнику пойдет ток в направлении э.д.с.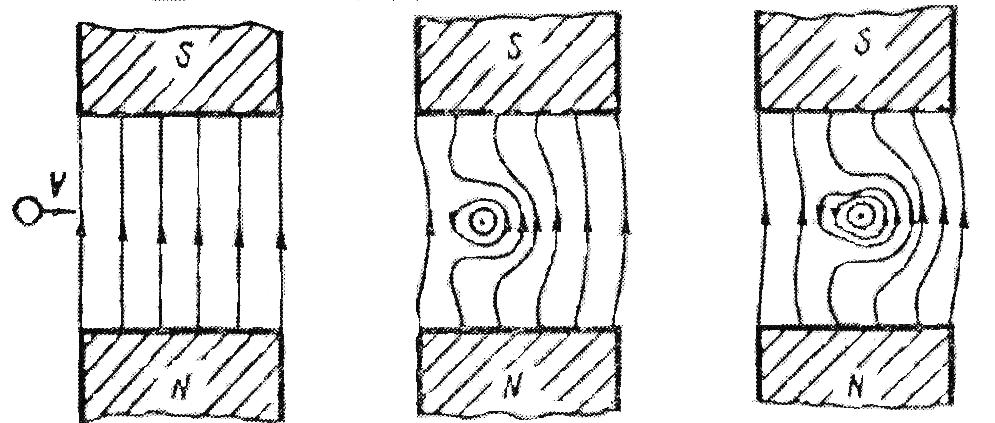 а б в Рис. 1.5. взаимодействие проводника с током и магнитного поля. Направление э.д.с. определяется правилом «правой руки». Кроме этого правила, полезно знать правило Миткевича, которое формулируется так: направление индуцированной э.д.с. и тока определяется деформацией поля по правилу буравчика (правого винта). Электромагнитная сила направлена в сторону ослабленного поля. Линии магнитного поля мнемонически ведут себя подобно упругим нитям и стремятся к сокращению действия электромагнитной силы. Явление электромагнитной индукции лежит в основе преобразования механической энергии в электрическую и наоборот. Действительно, электромагнитная мощность равна произведению электромагнитной силы на скорость перемещения проводника, т.е. 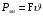 . .Так как по закону Ампера 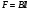 , а , а 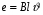 , то , то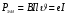 , ,Таким образом, электромагнитная мощность равна произведению э.д.с. на величину тока. Из этого уравнения следует возможность преобразования электрической мощности в механическую и обратно. Если замкнутый проводник, расположенный перпендикулярно магнитному полю, привести в движение со скоростью 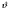 за счет внешней механической силы, то при этом возникает электрический ток, создающий тормозящую электромагнитную силу,- происходит преобразование механической энергии в электрическую (генераторный). Если же проводник питать от внешнего источника тока, то возникает ускоряющая электромагнитная сила, уравновешивающая внешнюю тормозящую силу, т.е. происходит обратный процесс преобразования электрической энергии в механическую (двигательный). за счет внешней механической силы, то при этом возникает электрический ток, создающий тормозящую электромагнитную силу,- происходит преобразование механической энергии в электрическую (генераторный). Если же проводник питать от внешнего источника тока, то возникает ускоряющая электромагнитная сила, уравновешивающая внешнюю тормозящую силу, т.е. происходит обратный процесс преобразования электрической энергии в механическую (двигательный).По Фарадею э.д.с. возникает вследствие пересечения проводником силовых линий магнитного поля. Максвелл рассматривал э.д.с. в замкнутом контуре и показал, что э.д.с. равна скорости изменения магнитного потока 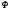 , сцепленного с контуром, , сцепленного с контуром,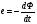 . .Магнитный поток 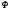 равен площади, ограниченной контуром, умноженной на среднее значение нормальной составляющей индукции, равен площади, ограниченной контуром, умноженной на среднее значение нормальной составляющей индукции,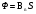 . .Положительной принята э.д.с., возникающая при убывании потока, т.е. когда приращение 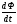 отрицательно. Отрицательный знак в приведенной формуле принят согласно закону инерции магнитного потока. При исчезновении тока возникает э.д.с., стремящаяся поддержать исчезающий ток, и, наоборот, при возникновении тока э.д.с., препятствующая возрастанию тока. отрицательно. Отрицательный знак в приведенной формуле принят согласно закону инерции магнитного потока. При исчезновении тока возникает э.д.с., стремящаяся поддержать исчезающий ток, и, наоборот, при возникновении тока э.д.с., препятствующая возрастанию тока.Можно доказать, что обе эти формулировки закона электромагнитной индукции эквивалентны, если рассматриваются замкнутые цепи. Из формулировки Фарадея следует, что при движении в магнитном поле проводника длиною в 1 м возникает напряженность электрического поля, равная векторному произведению: 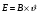 . .Из формулировки Максвелла следует, что для возникновения э.д.с. не обязательно нужен замкнутый контур проводника. Можно рассматривать любой воображаемый контур в пространстве. При изменении потока в этом контуре будет возникать индуцированное электрическое поле. 1.4.ЭЛЕКТРИЧЕСКИЕ И МАГНИТНЫЕ ЦЕПИ ПОСТОЯННОГО ТОКА При передаче электрической энергии от генераторов к потребителям образуется замкнутые электрические цепи тока. В цепь входят генератор, линия передачи, потребители. Генератор постоянного тока создает э.д.с., под действием которой в замкнутой цепи протекает ток. По закону Ома ток прямо пропорционален э.д.с 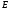 и обратно пропорционален полному сопротивлению цепи и обратно пропорционален полному сопротивлению цепи 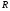 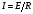 Основным сопротивление цепи является полезное сопротивление потребителя (например, лампа накаливания, электрическая печь). Внутреннее сопротивление генератора и сопротивление линии передачи должны быть по возможности минимальными для уменьшения потерь энергии, поскольку электрический ток, проходя по проводам, нагревает их. При этом электрическая энергия превращается в тепловую, которая рассеивается в окружающем пространстве, не выполняя полезной работы, т.е. представляет потерю энергии. Мощность потерь электрической энергии пропорционально квадрату тока и сопротивлению цепи 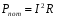 Сопротивление проводника постоянного тока зависит от материала, пропорционально его длине 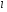 и обратно пропорциональна поперечному сечению и обратно пропорциональна поперечному сечению 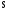 , т.е. , т.е.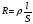 , ,где 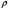 - удельное сопротивление материала проводника. - удельное сопротивление материала проводника.Для уменьшения потерь энергии желательно использовать материалы с малым удельным сопротивлением. Минимальное удельное сопротивление имеют серебро и медь, однако серебро – дорогостоящий металл, поэтому в настоящее время самыми распространенными проводниками является медь и алюминий. Перспективным для снижения потерь энергии является использование явления сверхпроводимости, открытого Х. Камерлинг-Оннесом в 1911 г. Оно заключается в том, что вблизи температуры абсолютного нуля (-273,16 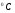 ) удельное электрическое сопротивление некоторых металлов падает до нуля. Уменьшение сопротивления происходит почти скачкообразно в пределах разности температур 0,01 ) удельное электрическое сопротивление некоторых металлов падает до нуля. Уменьшение сопротивления происходит почти скачкообразно в пределах разности температур 0,01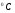 . Многие металлы, их сплавы и соединения переходят в состояние сверхпроводимости и при температурах несколько выше абсолютного нуля. Сверхпроводники теряют свойство сверхпроводимости, когда индукция магнитного поля на их поверхности превысит определение для данного металла и данной температуры критическое значение. До сих пор самые высокие температуры и критические поля наблюдались в соединениях . Многие металлы, их сплавы и соединения переходят в состояние сверхпроводимости и при температурах несколько выше абсолютного нуля. Сверхпроводники теряют свойство сверхпроводимости, когда индукция магнитного поля на их поверхности превысит определение для данного металла и данной температуры критическое значение. До сих пор самые высокие температуры и критические поля наблюдались в соединениях 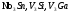 , однако, они слишком хрупкие и дорогие. Поэтому в настоящее время широкое применение получил сплав ниобия с цирконием, легко поддающийся пластической обработке. , однако, они слишком хрупкие и дорогие. Поэтому в настоящее время широкое применение получил сплав ниобия с цирконием, легко поддающийся пластической обработке.В неразветвленной электрической цепи алгебраическая сумма э.д.с. равна сумме падений напряжения на всех элементах цепи. Аналогичный закон справедлив и для магнитный цепей: в замкнутом контуре магнитной цепи сумма намагничивающих сил равна сумме произведений напряженности магнитного поля на длину участка магнитной цепи, т.е. 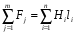 , ,где 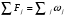 - сумма произведений токов на число витков. - сумма произведений токов на число витков.Выразив 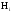 через величину индукции - через величину индукции - 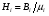 и учитывая, что в неразветвленной магнитной цепи поток и учитывая, что в неразветвленной магнитной цепи поток 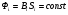 (здесь (здесь 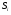 - площадь поперечного сечения магнитопровода), получим соотношение для магнитной цепи, аналогичное закону Ома для электрической цепи - площадь поперечного сечения магнитопровода), получим соотношение для магнитной цепи, аналогичное закону Ома для электрической цепи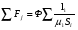 , ,или 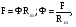 где 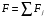 - сумма намагничивающих сил; - сумма намагничивающих сил; 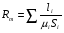 - сумма магнитных сопротивлений последовательно включенных участков магнитной цепи. - сумма магнитных сопротивлений последовательно включенных участков магнитной цепи.По форме выражение для тока в электрической цепи подобно выражению для потока в магнитной цепи. Существенное различие состоит в том, что электрическое сопротивление обычно мало зависит от тока и может считаться постоянным, а магнитное сопротивление от магнитной проницаемости данного элемента цепи. 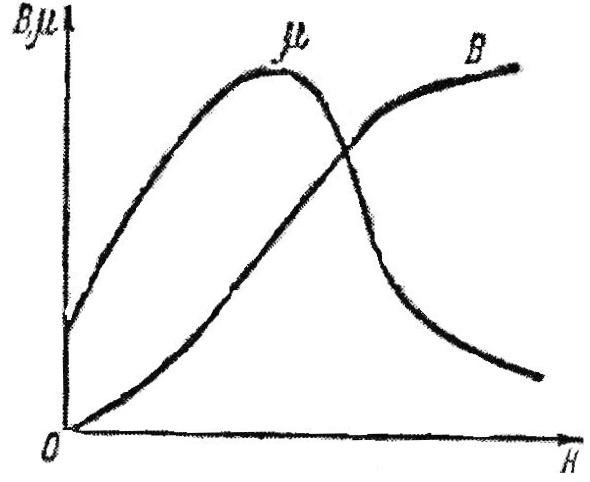 Рис. 1,6 зависимость магнитной проницаемости 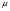 и индукции и индукции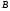 от напряженности магнитного поля 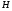 для ферромагнитных для ферромагнитных материалов. В свою очередь магнитная проницаемость зависит от напряженности, а следовательно, от магнитного потока (рис. 1.6). Поэтому при расчете магнитной цепи задаются потоком 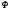 , по его величине определяют индукцию в отдельных элементах цепи путем деления , по его величине определяют индукцию в отдельных элементах цепи путем деления 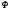 на площадь сечения на площадь сечения 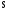 . Затем по кривым намагничивания . Затем по кривым намагничивания 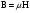 находят напряженность поля находят напряженность поля 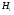 , умножают ее на длину участка , умножают ее на длину участка 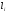 и, суммируя и, суммируя 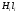 по всей цепи находят намагничивающую силу для заданного значения потока. по всей цепи находят намагничивающую силу для заданного значения потока.1.5. ЦЕПИ ПЕРЕМЕННОГО ТОКА Переменный ток вырабатывается генератором переменного тока – электрической машиной, обычно состоящей из трехфазного статора и ротора. Ротор может возбуждаться постоянным током – в это случае машина будет синхронной, т.е. вращение ротора и магнитного поля синхронное, или переменным током – в этом случае машина асинхронная, т.е. частота вращения ротора выше частоты вращения магнитного поля. В любом случае в обмотках статора по закону электромагнитной индукции индуцируется трехфазной переменный ток заданной частоты. Наиболее целесообразной формой тока является синусоидальная, что достигается специальным устройством обмоток на статоре. Мгновенное значение тока 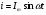 , ,где 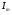 - амплитуда тока; - амплитуда тока; 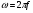 - угловая частота. - угловая частота.Стандартная промышленная частота государств может отличаться от 50 Гц. При протекании тока по контуру, состоящему из нескольких витков, создается магнитный поток, связанный со всеми витками. Этот поток называется потокосцеплением и определяется по формуле 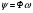 , ,где 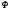 - поток, создаваемый одним витком. Потокосцепление пропорционально тока и коэффициенту самоиндукции (индуктивности) - поток, создаваемый одним витком. Потокосцепление пропорционально тока и коэффициенту самоиндукции (индуктивности)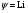 . .Индуктивность определяется как частное от деления потокосцепления на ток 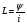 и характеризует способность контура записать магнитную энергию. Индуктивность в линейных цепях величина постоянная. В контурах с ферромагнитным сердечником при изменении тока в контуре магнитная проницаемость, а следовательно, и магнитное сопротивление меняются, поэтому зависимость потока от тока является нелинейной. При переменном токе в контуре возникает э.д.с. самоиндукции, уравновешивающая напряжение, приложенное к контуру, активным сопротивлением которого можно пренебречь: 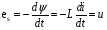 . .При постоянном токе э.д.с. самоиндукции отсутствует и приложенное постоянное напряжение уравновешивается омическим падение напряжения на активном сопротивлении: 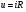 . .В более общем случае при переменном токе приложенное к цепи внешнее напряжение уравновешивается активным падением напряжения и э.д.с. самоиндукции, т.е. 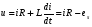 . .Если 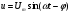 , то должен возникнуть установившийся ток , то должен возникнуть установившийся ток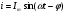 , ,амплитуда которого равна напряжению, деленному на полное сопротивление цепи, а фаза отставания тока от напряжения определяется отношением индуктивного и активного сопротивления: 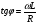 . .В общем случае электрическая цепь состоит из активного сопротивления 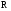 , катушки индуктивности , катушки индуктивности 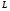 и конденсатора емкостью и конденсатора емкостью 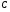 (рис. 1.7). Конденсатор проводит переменный ток (рис. 1.7). Конденсатор проводит переменный ток 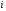 за счет изменения электрического поля во времени (ток смещения). за счет изменения электрического поля во времени (ток смещения).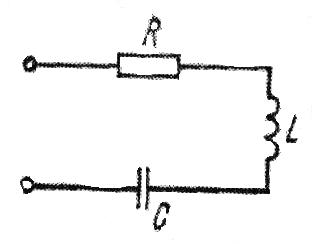 Рис. 1.7 цепь с последовательно соединенными активным сопротивлением, индуктивностью и емкостью. Если известен ток, можно найти заряд конденсатора 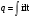 , , а зная емкость 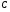 , нетрудно определить напряжение на конденсаторе , нетрудно определить напряжение на конденсаторе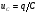 . .Тогда уравнение равновесия напряжений в цепи будет иметь вид 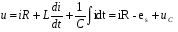 . .При синусоидальном приложенном напряжении в цепи устанавливается ток 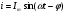 амплитудой амплитудой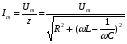 , ,где  - полное сопротивление цепи; - полное сопротивление цепи; 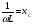 - емкостное сопротивление; - емкостное сопротивление; 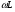 - индуктивное сопротивление. - индуктивное сопротивление.Результирующее реактивное сопротивление равно разности индуктивного и емкостного сопротивлений 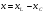 , ,Поэтому при определенных величинах частоты и емкости 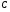 результирующее реактивное сопротивление может обратиться в нуль. Происходит явление резонанса напряжений, т.е. полная компенсация индуктивного сопротивления емкостным. В результате ток значительно возрастает, так как его величина будет определяться только активным сопротивлением результирующее реактивное сопротивление может обратиться в нуль. Происходит явление резонанса напряжений, т.е. полная компенсация индуктивного сопротивления емкостным. В результате ток значительно возрастает, так как его величина будет определяться только активным сопротивлением 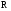 . .Наличие реактивных сопротивлений в цепи влияет не только на величину тока, но и приводит к сдвигу тока во времени (по фазе) по отношению к приложенному напряжению. Величина угла сдвига 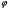 определяется по выражению определяется по выражению 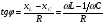 . .В зависимости от характера полного сопротивления угол 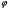 может изменяться от может изменяться от 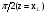 до до 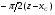 . Большинство приемников электрической энергии имеет активно-индуктивное сопротивление, поэтому для них угол . Большинство приемников электрической энергии имеет активно-индуктивное сопротивление, поэтому для них угол 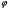 лежит в пределах от 0 до лежит в пределах от 0 до 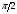 . .При этом полный ток 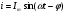 может рассматриваться как сумма активного тока может рассматриваться как сумма активного тока 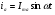 , совпадающего по фазе относительно напряжения на четверть периода. , совпадающего по фазе относительно напряжения на четверть периода.Амплитуда активного тока 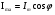 , реактивного тока , реактивного тока 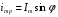 . .Активная составляющая тока определяет мощность, передаваемую по цепи 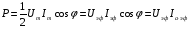 , ,где 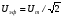 и и 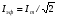 - эффективные (действующие) значения напряжения тока. - эффективные (действующие) значения напряжения тока.Величину 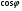 называют коэффициентом мощности. В силовых цепях называют коэффициентом мощности. В силовых цепях 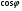 стремятся приблизить к единице для уменьшения потерь в сетях, генераторах и их элементах. стремятся приблизить к единице для уменьшения потерь в сетях, генераторах и их элементах. |
