Практическая работа 5. Вычисление площадей и периметров многоуго. Вычисление площадей и периметров многоугольников
 Скачать 35.15 Kb. Скачать 35.15 Kb.
|
|
Практическая работа 5. Тема: Вычисление площадей и периметров многоугольников Цель: Закрепить и систематизировать знания по теме «Многоугольники». Ход работы 1. Проверка готовности к практической работе: устный опрос. 2. Выполнение заданий. 1) Для того чтобы выполнить практическую работу, необходимо выбрать соответствующие задания по вашему варианту. 2) Опираясь на теоретический материал, тренировочные упражнения на уроке и домашнее задание, произвести расчет заданий 3. Ответить на контрольные вопросы. Справочные материалы Трапеция Трапеция - четырёхугольник, у которого две стороны параллельны (основания трапеции), а две другие - непараллельны (боковые стороны трапеции). Отрезок, соединяющий середины боковых сторон, называется средней линией трапец. 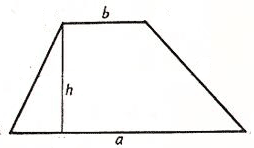 Формула площади трапеции: Площадь геометрической фигуры - часть поверхности, ограниченная замкнутым контуром данной фигуры. Величина площади трапеции выражается числом заключающихся в него квадратных единиц. 1) Площадь трапеции равна произведению полусуммы ее оснований на высоту (a, b, h). 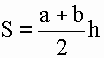 S - площадь трапеции a - длина 1-ого основания b - длина 2-ого основания h - длина высоты трапеции Формула периметра трапеции: Периметр геометрической фигуры - суммарная длина границ плоской геометрической фигуры. Периметр имеет ту же размерность величин, что и длина. 1) Периметр трапеции равен сумме 4-х её сторон (a, b, c, d). P - периметр трапеции a, c - длины оснований трапеции b, d - длины боковых сторон трапеции Ромб Ромб - это четырёхугольник, у которого все стороны равны. Ромб можно рассматривать как частный случай параллелограмма, у которого или две смежные стороны равны, или диагонали взаимно перпендикулярны, или диагональ делит угол пополам. Ромб с прямыми углами называется квадратом. 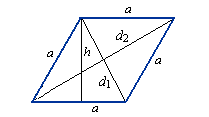 Формулы площади ромба: Площадь геометрической фигуры - часть поверхности, ограниченная замкнутым контуром данной фигуры. Величина площади ромба выражается числом заключающихся в него квадратных единиц. 1) Площадь ромба равна произведению длины его стороны на высоту (a, h). 2) Площадь ромба равна половине произведения его диагоналей. 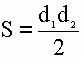 S - площадь ромба a - длина основания ромба h - длина высоты ромба d1 - длина 1-ой диагонали d2 - длина 2-ой диагонали Формула периметра ромба: Периметр геометрической фигуры - суммарная длина границ плоской геометрической фигуры. Периметр имеет ту же размерность величин, что и длина. 1) Периметр ромба равен сумме 4-х длин его сторон или произведению длины любой его стороны на четыре (так как у ромба длины всех сторон равны). P - периметр ромба a - длина стороны ромба Параллелограмм Параллелограмм - это четырёхугольник, у которого противолежащие стороны попарно параллельны, т.е. лежат на параллельных прямых. Частными случаями параллелограмма являются прямоугольник, квадрат и ромб. 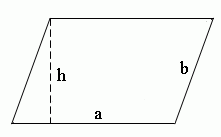 Смежные стороны параллелограмма - стороны, имеющие общую вершину Формула площади параллелограмма: Площадь геометрической фигуры - часть поверхности, ограниченная замкнутым контуром данной фигуры. Величина площади параллелограмма выражается числом заключающихся в него квадратных единиц. 1) Площадь параллелограмма равна произведению длины его основания на длину высоты (a, h). S - площадь параллелограмма a - длина основания h - длина высоты Формула периметра параллелограмма: Периметр геометрической фигуры - суммарная длина границ плоской геометрической фигуры. Периметр имеет ту же размерность величин, что и длина. 1) Периметр параллелограмма равен удвоенной сумме 2-х его смежных сторон (a, b). P - периметр параллелограмма a - длина 1-ой стороны параллелограмма b - длина 2-ой стороны параллелограмма Варианты практической работы Вариант 1. Диагонали ромба равны 18 м и 24 м. Найти периметр ромба и расстояние между параллельными сторонами. Сторона ромба равна 50, а диагональ равна 80. Найдите площадь ромба. Контрольные вопросы 1 . Что называется многоугольником? 2. Что называется трапецией, ромбом? 5. Дайте определение смежным сторонам параллелограмма. Критерии оценивания
| |||||||||||||||||
