Вычислительная математика
 Скачать 0.74 Mb. Скачать 0.74 Mb.
|
|
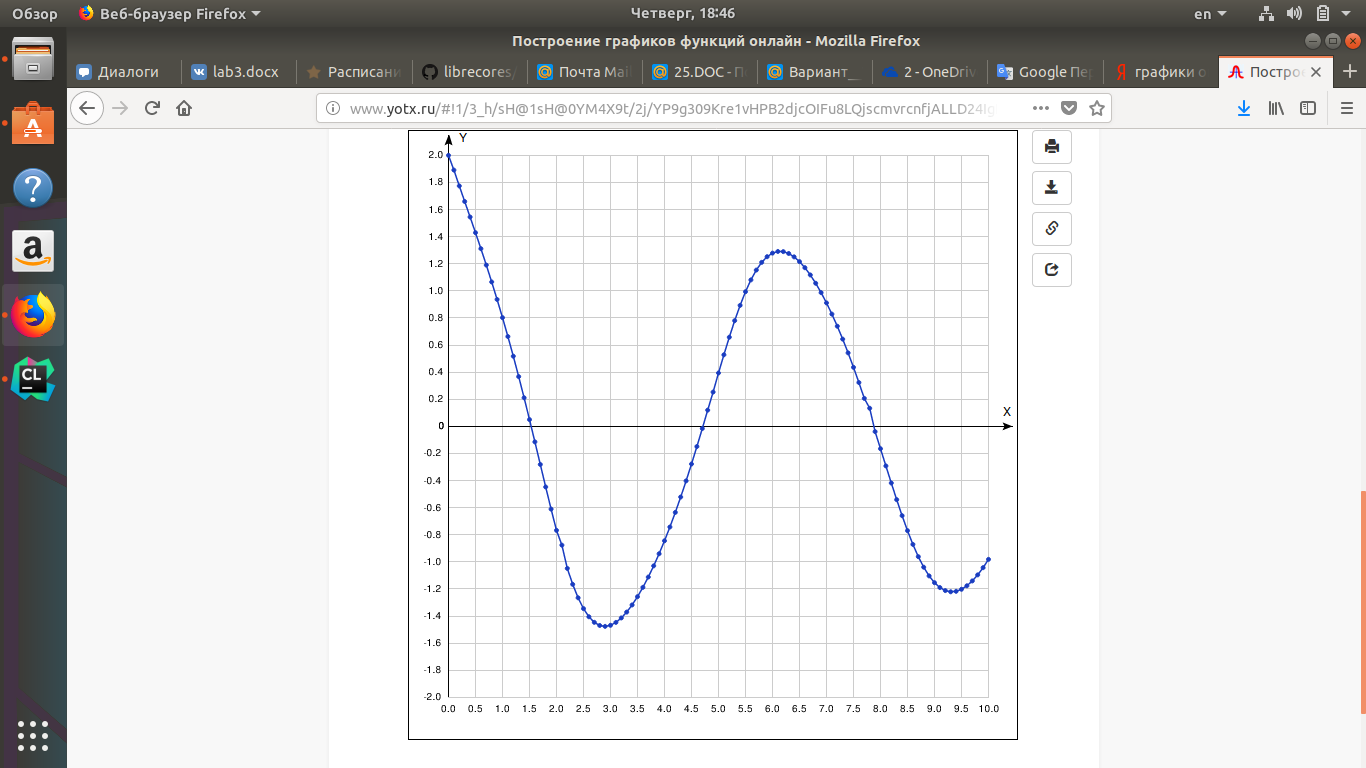
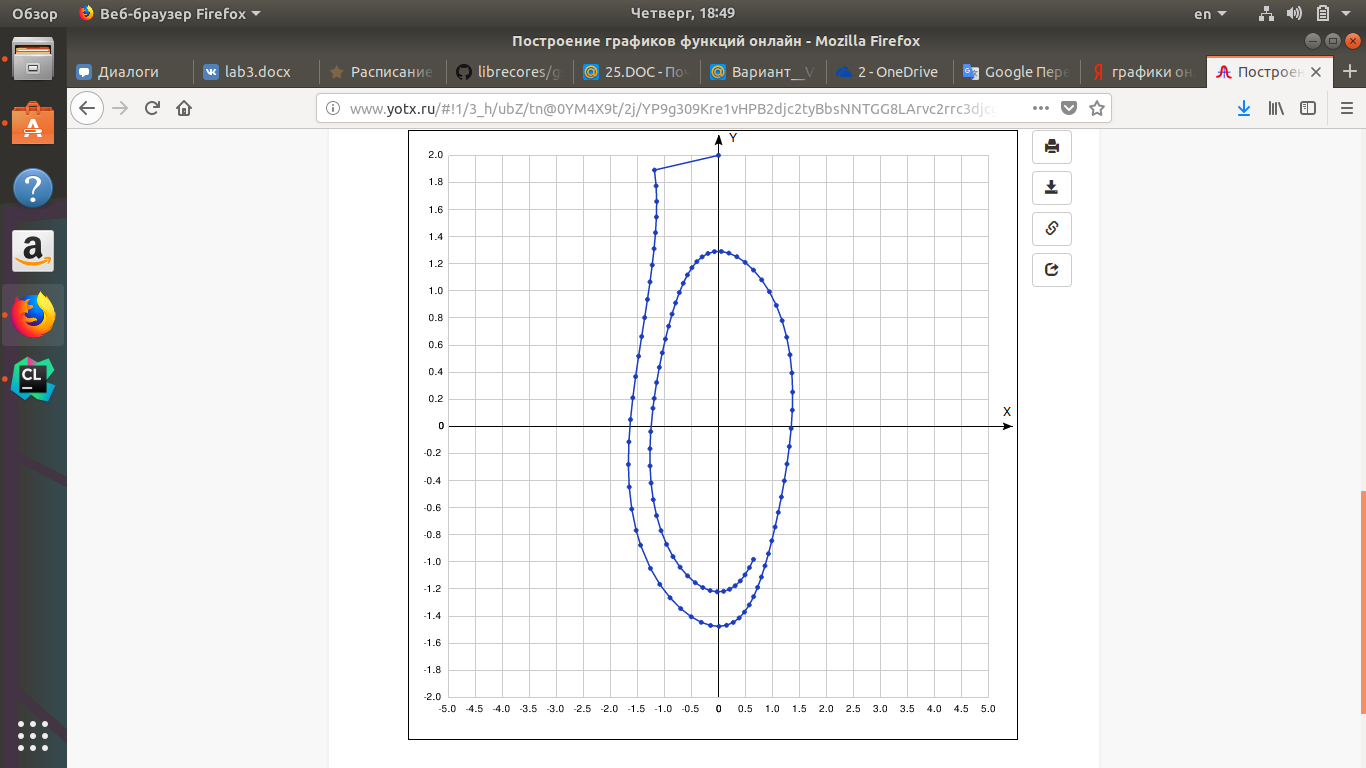
Санкт-Петербургский государственный политехнический университет Институт компьютерных наук и технологий Кафедра «Компьютерные системы и программные технологии» КУРСОВАЯ РАБОТА Разработка программы для исследования осциллятора Ван дер Поля с запаздывающей амплитудой по дисциплине «Вычислительная математика» Выполнил студент гр.23531/3 _________П.Р. Малахов Руководитель доцент, к.т.н. _________ В.Н. Цыган «___» __________ 2018 г. Санкт-Петербург 2018 Санкт-Петербургский государственный политехнический университет ЗАДАНИЕ НА ВЫПОЛНЕНИЕ КУРСОВОЙ РАБОТЫ студенту группы 23531/3 Малахову Павлу Романовичу (номер группы) (фамилия, имя, отчество) 1. Тема работы: Разработка программы для исследования осциллятора Ван дер Поля с запаздывающей амплитудой 2. Срок сдачи законченного проекта (работы) 4 июня 2018 г. 3. Исходные данные к проекту (работе): Общий вид системы дифференциальных уравнений, описывающих свободные колебания осциллятора Ван дер Поля с запаздывающей амплитудой; начальные условия для решения; рекомендованный шаг исследования численного решения дифференциального уравнения; перечень заданных преподавателем параметров уравнения с указанием уравнений или соотношений для их нахождения (вариант К-3-25). 4. Содержание пояснительной записки (перечень подлежащих разработке вопросов): введение, основная часть (вычисление значений заданных преподавателем параметров дифференциального уравнения; анализ результатов; влияние погрешности на результат), заключение, список использованных источников, приложение 1(код программы). Дата получения задания: «01» марта 2018 г. Руководитель _______________В.Н. Цыган (инициалы, фамилия) (подпись) Задание принял к исполнению ______________П.Р. Малахов (инициалы, фамилия) (подпись студента) ____________ (дата) Содержание 1.Введение…………………………………………………………….…………………3 1.1 Задание…………………………………………..…..………..………….3 2. Основная часть…………………………………….………………………………….4 1. Вычисление значений параметров дифференциального уравнения…………………………………………………………………..4 2. Вывод программы..……………...…………………………………………5 3. Графики и анализ погрешности…..…………………...…………..……...7 3.Заключение………………………………………………………………….……......8 1.Список использованной литературы……………...........……………….9 2. Приложение 1(код программы)…………………………….….…….....10 1. Введение: В данной курсовой работе рассматриваются вопросы применения методов вычислительной математики для решения задачи параметрической идентификации объекта. Целью работы является разработка программ, позволяющих на основе математического описания объекта оценить емкость конденсатора в электрической цепи. При разработке собственных программ использовались стандартные библиотечные программы численного интегрирования, решения систем дифференциальных уравнений и др. Выполнение курсовой работы позволяет закрепить теоретические знания путем решения практической инженерной задачи. 1.1 Задание  2.1 Вычисление значений параметров дифференциального уравнения Для решения поставленной задачи был выбран язык C++. При выполнении задания была использована следующая вспомогательная программа: RKF45 – программа решения системы дифференциальных уравнений первого порядка методом Рунге-Кутты 4-ой степени. Приведем систему дифференциальных уравнений 2-го порядка к системе уравнений 1-го порядка. Искусственно введем переменную y: v` = y; z` = (v^2 — z) / Ƭ; y`=2μ[(1 — z)y — z`v] – ω0v. Найдем начальные условия, которые в будущем подставим в RKF45(): 1) C помощью программ DECOMP() & SOLVE() решаем заданную систему уравнений, находим коэффициенты A, B, C: A = 2; B = 0; C = 1. 2) Затем будем искать ω0. С помощью программы quanc8() посчитаем значение интеграла и умножим его на коэффициент k= 0.9517245 . Таким образом, ω0 = 1. 3) После этого найдем . Для этого с помощью программы ZEROIN() найдем корни уравнения 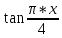 =x+3 , выберем наименьший положительный корень и умножим на коэффициент k1= 0.05763710. =x+3 , выберем наименьший положительный корень и умножим на коэффициент k1= 0.05763710.Таким образом, =0,01. Найденные коэффициенты подставим в систему дифференциальных уравнений и решим её с помощью RKF45(). 2.2 Вывод программы: 1)Значения параметров: 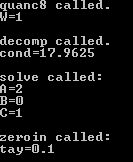 Решение системы дифференциальных уравнений : 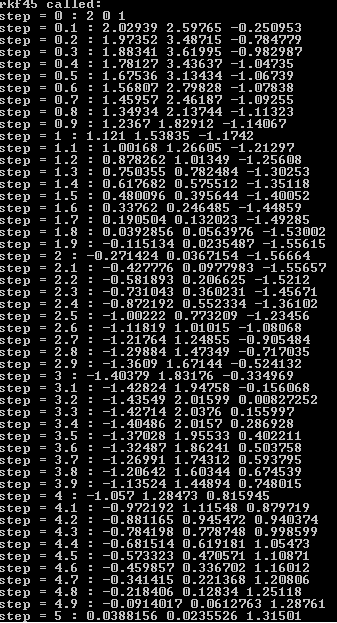 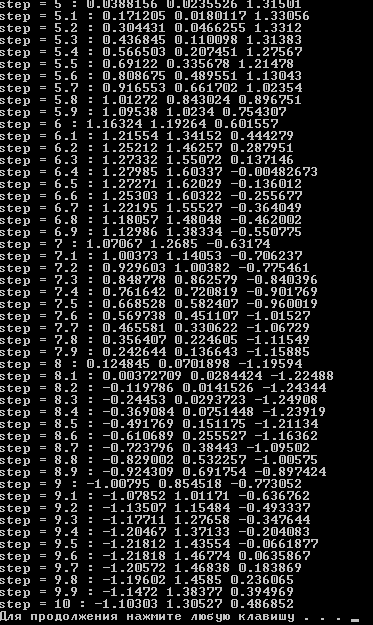 2.3 Графики и анализ погрешности: Построены графики функций V(t) и V(V`) в промежутке t: от 0 до 10.
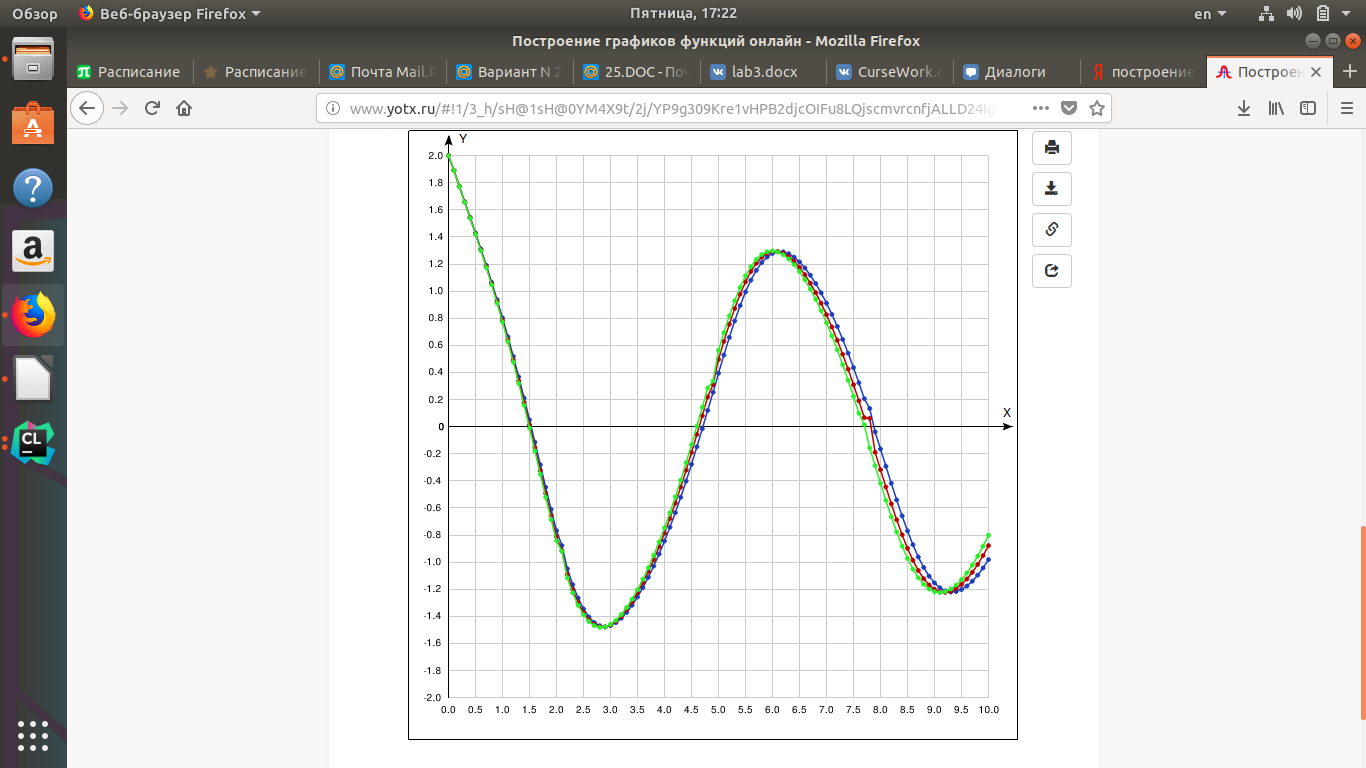
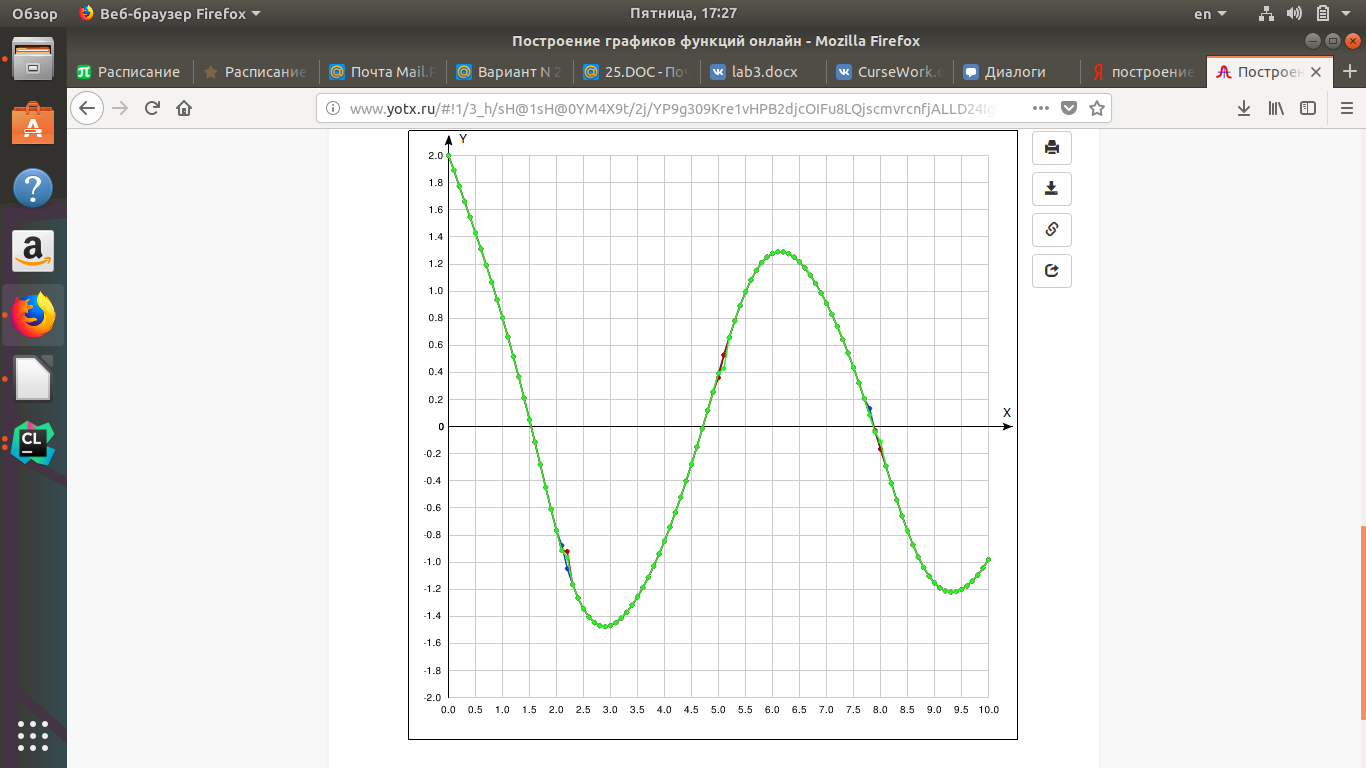
Погрешность V(t) будем искать следующим образом: Найдем среднеквадратичное отклонение и умножим на коэффициент Стьюдента. Полученная погрешность равна ∆V = 0.140336 В. Изменим значения ω0 и Ƭ на 3% и 5% , чтобы определить обусловленность системы. Рассмотрим график функций V(t):
3 Заключение Благодаря проделанной работе, была изучена система уравнений для исследования осциллятора Ван дер Поля, было выявлено, что метод Рунге-Кутты 4-ой степени является точным. Вызов RKF45 с измененными начальными условиями приводит к получению таких результатов при которых наша система является устойчивой к небольшим изменениям в начальных условиях и они не оказывают существенной роли на решение. Рассмотрев полученный график V(t), мы можем сказать, что график V(t) является тригонометрическим, а V(V`) - образует «кольцо», следовательно можно утверждать, что V(t) — действительно, колебательная система. 3.1 Список используемой литературы 1. Устинов С.М., Зимницкий В.А. Вычислительная математика. – СПб.: БХВ Петербург, 2009. – 336 с.: ил. – (Учебное пособие). 2. Решение уравнений https://www.kontrolnaya-rabota.ru - (Электронный ресурс) 3.2 Приложение 1 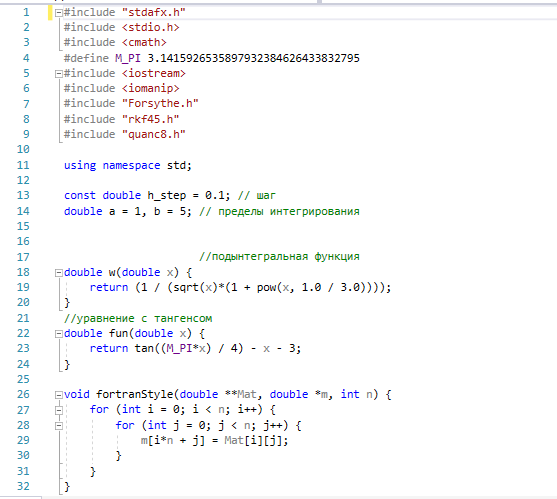 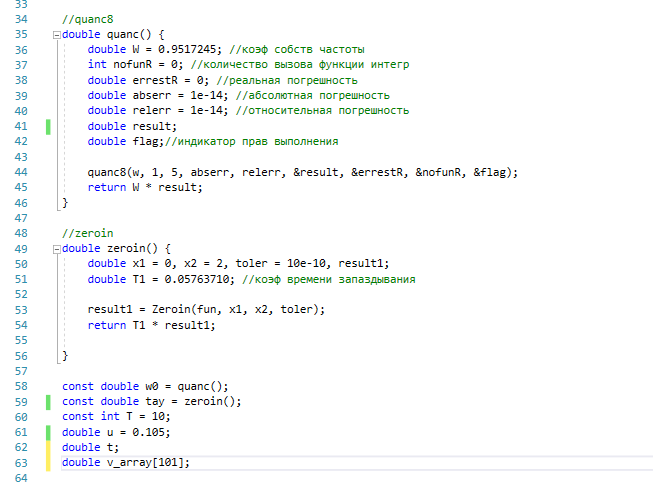 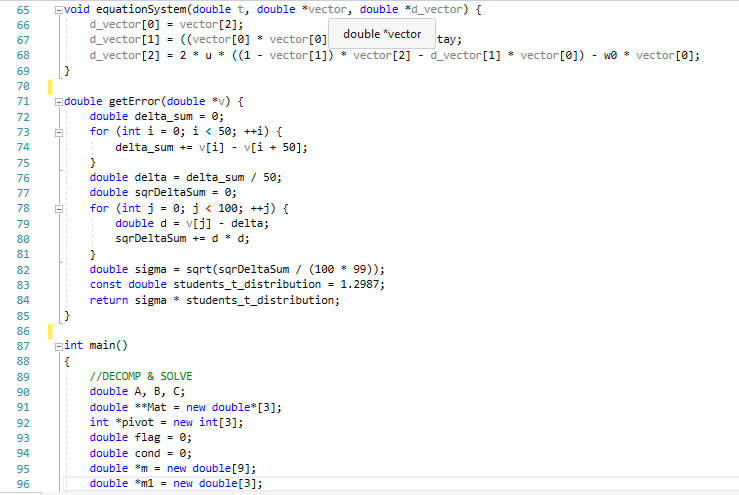 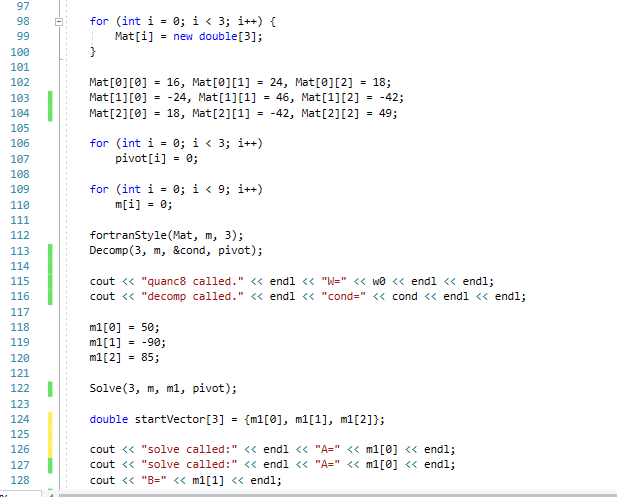  |