лекция 3. Выделение вязко пластический плиты и метод ее решения
 Скачать 363.61 Kb.
|
|
Выделение вязко пластический плиты и метод ее решения. Условие вязко пластичности отличается от условия пластичности обычно 1 или несколькими слагаемыми, отвечающие за вязкость. Вязкость обозначается ню. Если принять ню=0, т.е. вязкости нет, тогда по условию темы останется только пластическое состояние плиты. В этом случае пластичность обычно имеет вид жесткой пластичности, т.е. упругая часть тела не интересует на данном этапе. Для плоского состояния, в двумерной постановке задачи, когда все искомые функции зависят только от х и у, и не зависят от z, условие пластичности сводится к соотношению (сигма х – сигма у )^2=4k^2. В случае пространства это же соотношение можно записать по-другому соотношение пластичности становится переводимой из одной другой методом перестановки. О этих уравнений будет 3. Для пространственной задачи вязко-пастичности в каждом множестве добавляется слагаемое, отвечающее за вязкость. Константа k отвечает за пластичность, итого имееем 3 уравнения.  Очень многие уравнения такого сложного типа решить в чистом виде не представляется возможным, методы которыми решаются такие уравнения основы на небольших во сновном разновидностям и называются различными методами, например: метод линеаризции, пенелова, фурье, пошагового спуска, последовательных приближений, степ бай степ, рекуррентных соотношений. Основа почти всех методов – чтобы схватить основное отличие решения вытащить это отличие, а далее продолжать уточнять полученное решение, приближаясь шаг за шагом к искомому точному решению. Самый простой метод – это метод маклорейна, когда какую-либо функции. Выстраивают в ряд, но с неизвестными функциями это не всегда возможно.Сначала формула (3 потом 2) Обозначим за мю 1 выражение Мю 1 и мю 2 – это влияние пластичности 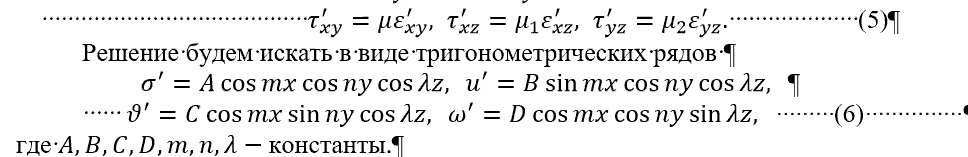 Сигма = 1/3 (сигма х + сигма у + сигма зед) 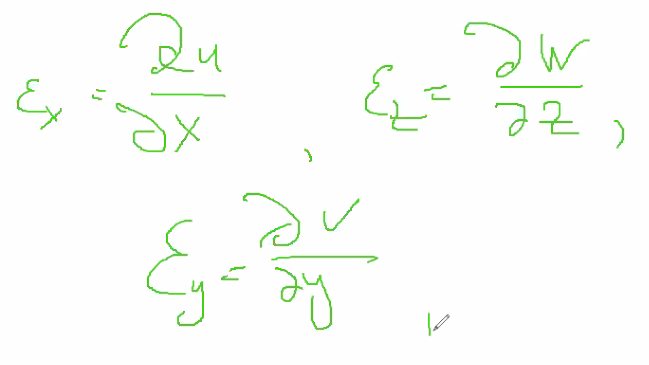 Уравнение 7 – уравнение равновесия 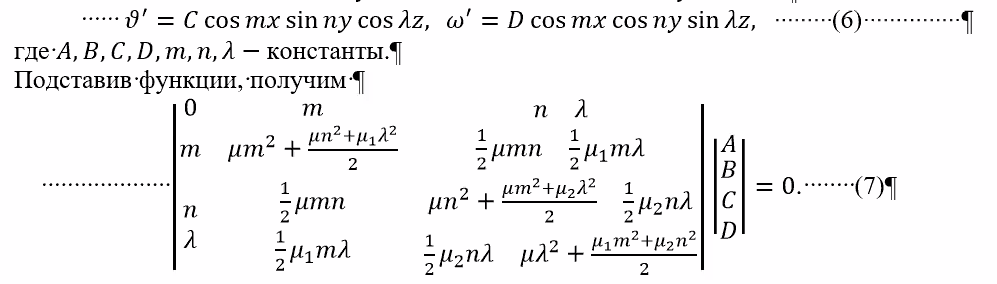 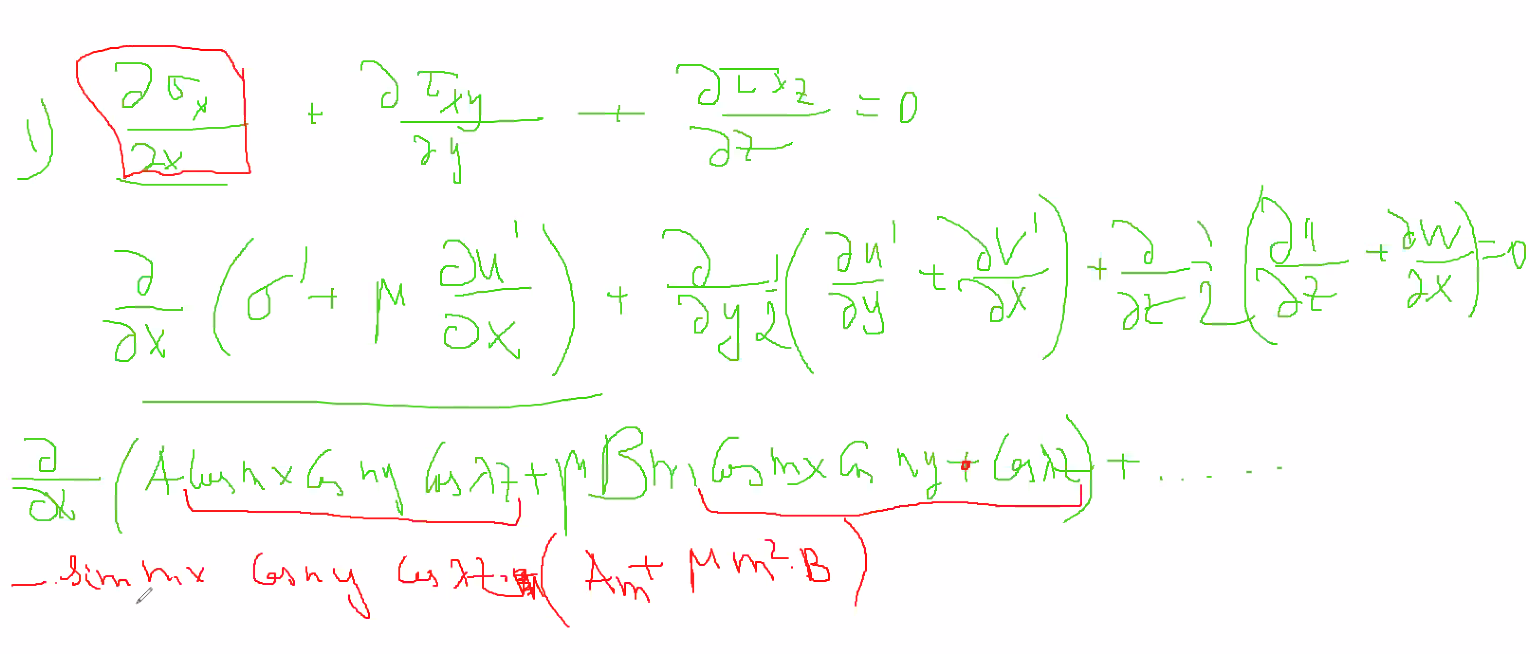 |