Лекция_7. Vii неустановившаяся фильтрация упругой жидкости в упругой пористой среде

• Название: Vii неустановившаяся фильтрация упругой жидкости в упругой пористой среде
• Дата: 24.01.2023
• Размер: 1.01 Mb.
• Имя файла: Лекция_7.doc
• Тип: Документы; #902874
• страница: 2 из 4

По правилу дифференцирования сложных функций находим

;
;
.
Подставляя найденные значения производных в уравнение (7.14), получаем обыкновенное дифференциальное уравнение
, (7.15)
которое должно быть проинтегрировано по условиям (7.13)

Для решения (7.15) обозначим , тогда уравнение (7.15) принимает вид

. (7.20)

Разделяя переменные в (7.20) и интегрируя, получаем
, (7.21)
где С₁ – постоянная интегрирования.

Интегрируя (7.21), будем иметь
- по первому условию из (7.13).

Второе условие из (7.13) дает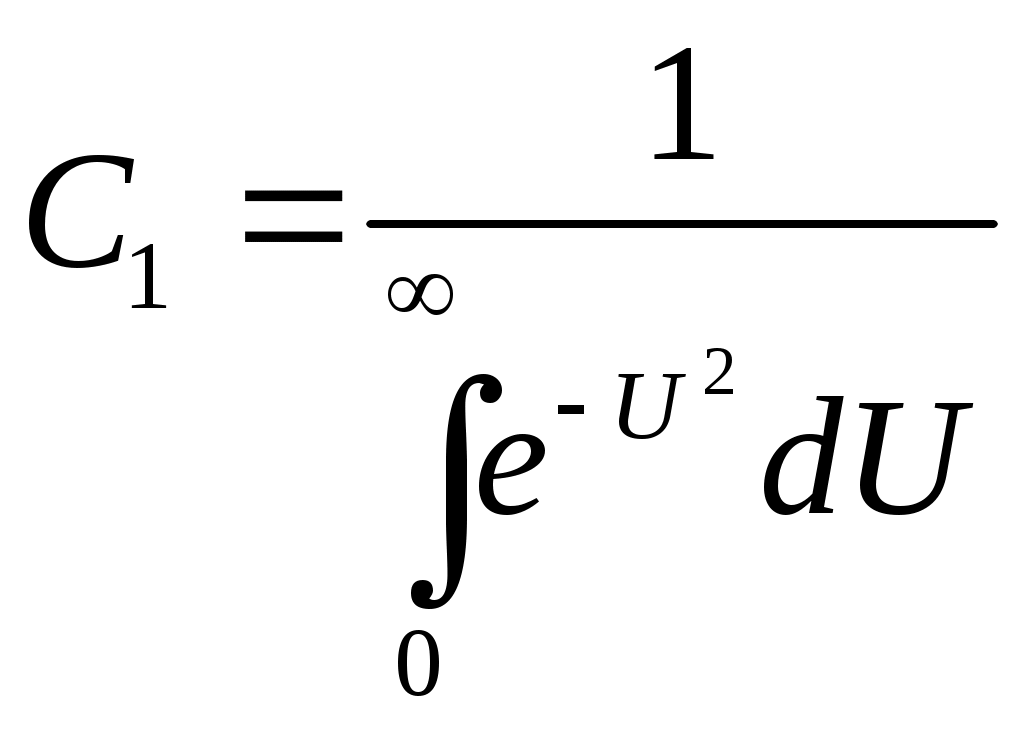

.

Из интегрального исчисления известно, что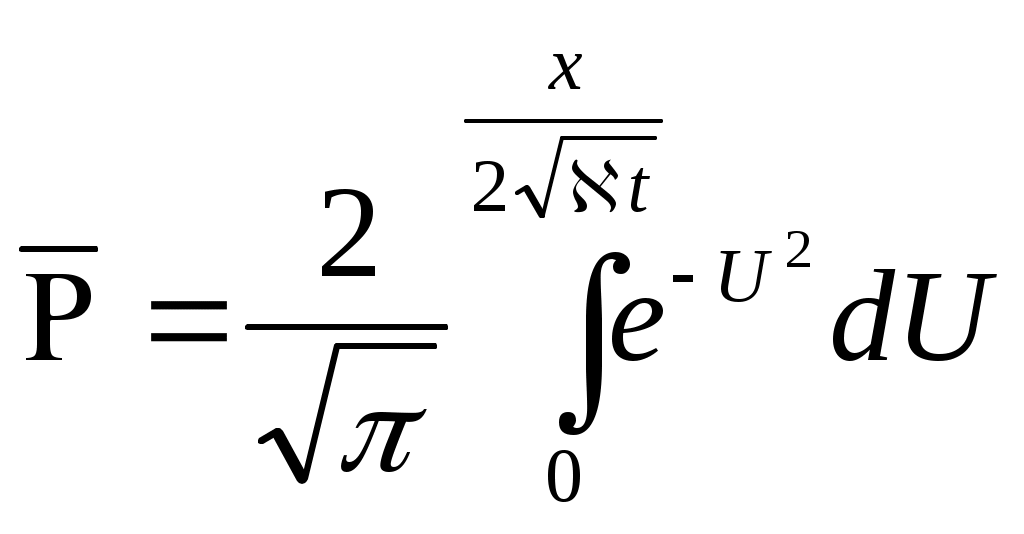
- интеграл Пуассона;
поэтому , а . (7.22)

Интеграл в (7.22) называется интегралом вероятности и является табулированной функцией, изменяющейся в пределах от 0 до 1: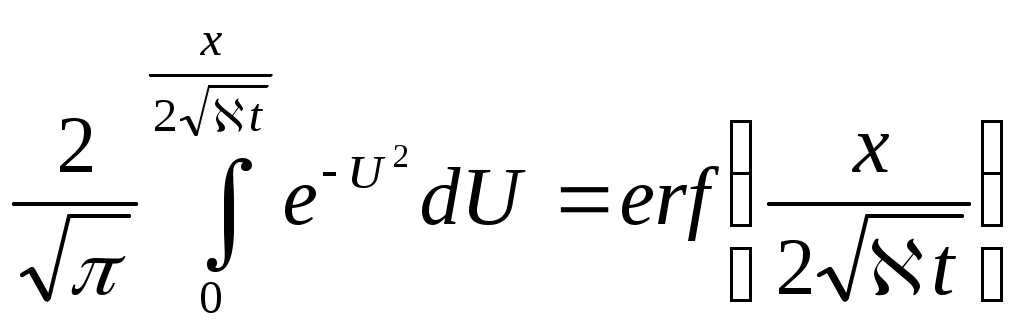
- интеграл вероятности или функция

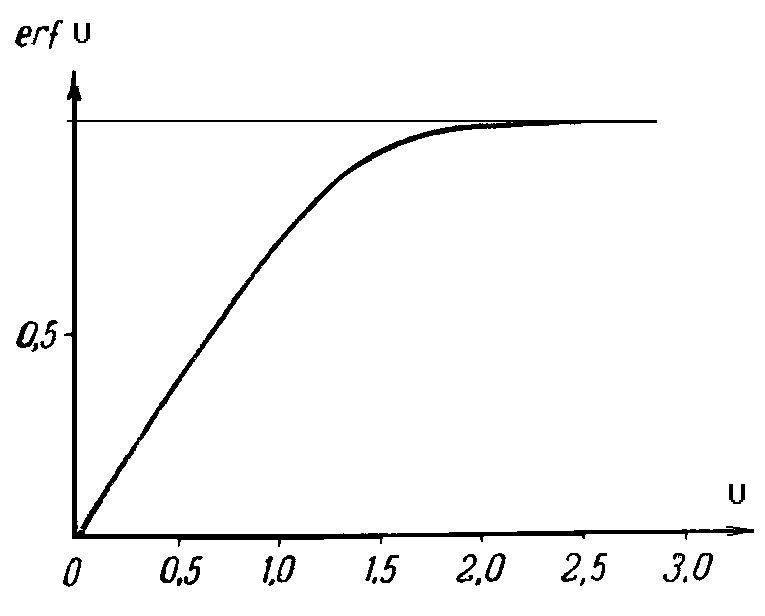Крампа (график функции представлен на рис.42)

Рис. 42

Таким образом

.

Тогда закон распределения давления в неустановившемся прямолинейно-параллельном потоке упругой жидкости имеет вид
. (7.23)

Зная х и t, определяем значение , а 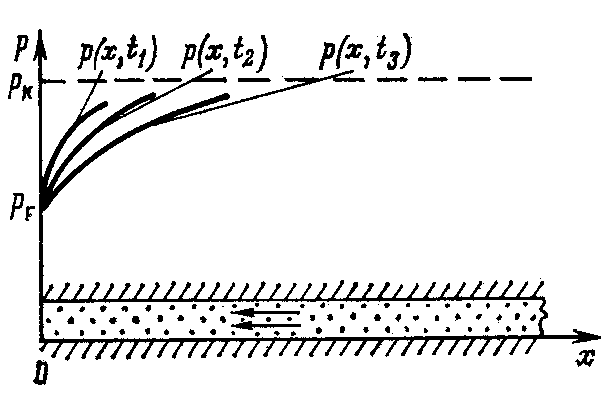затем из таблиц или из графика находим и находим по формуле (7.23) значение давления Р.

Р
аспределение давления Р(х,t) показано на рис.43.

Рис. 43

Найдем дебит Q галереи.

Будем считать положительным дебит, отбираемый из галереи (х=0), когда поток движется против оси х.

Согласно закону Дарси, имеем
,
где В, h – соответственно ширина и толщина пласта.

Дифференцируя выражение (7.23), получаем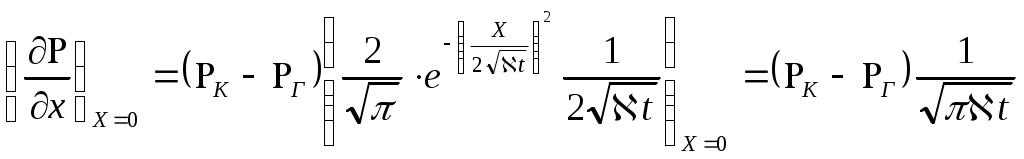
.

Тогда дебит будет равен

. (7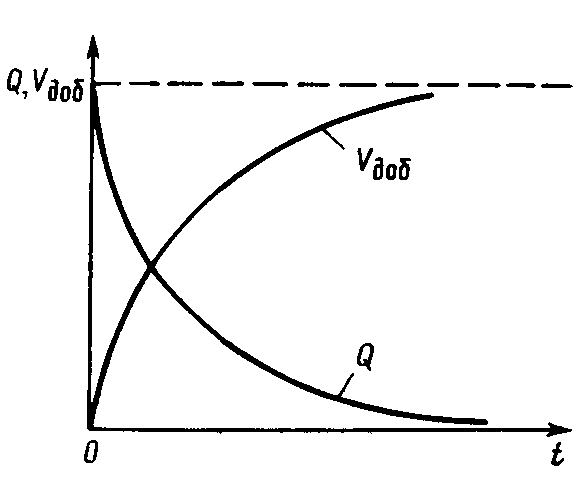.24)
И
з формулы (7.24) следует, что дебит галереи убывает с течением времени по закону и при t→  стремится к нулю.

Рис. 44

Накопленная к моменту времени t добыча V_доб определяется по формуле

т.е. сразу после начала отбора из галереи V_доб быстро возрастает, а затем растет очень медленно.

4. 
   Плоскорадиальный фильтрационный поток упругой жидкости; основная формула теории упругого режима
   

Пусть в неограниченном горизонтальном пласте постоянной толщины h имеется добывающая скважина нулевого радиуса (точечный сток). Начальное пластовое давление во всем пласте одинаково и равно Р_К. В момент времени t=0 скважина пущена с постоянным объемным дебитом Q₀=const. В пласте образуется неустановившийся плоскорадиальный поток упругой жидкости.

Распределение давления в пласте Р(r,t) определяется интегрированием уравнения (7.10), которое для плоскорадиального движения (в полярных координатах) запишется в виде

. (7.25)

Начальные и граничные условия задачи:

при t = 0;

при r ; (7.26)

при r=0, t0.

Последнее условие запишем в виде

. (7.27)

Проведем анализ размерностей.

Искомое распределение давления в пласте Р(r,t) зависит от пяти определяющих параметров: r, t, , P_K , Q/2kh , размерности которых следующие:

.

Тогда давление, приведенное к безразмерному виду зависит от двух безразмерных параметров (т.к. из пяти параметров три имеют независимые размерности – r, t, P_K: n = 5, k = 3, n-k = 2):

, (7.28)

где - безразмерный комплекс.

Таким образом, задача автомодельна и уравнение (7.27) можно свести к обыкновенному.

Дифференцируя (7.28), найдем аналогично предыдущему

;

;

.

Подставляя полученные выражения в уравнение (7.25), получаем обыкновенное дифференциальное уравнение вида

, (7.29)

которое нужно проинтегрировать при условиях, полученных из (7.26) и (7.27):

при

и . (7.30)

Используем подстановку , тогда вместо (7.29) будем иметь

,

или

. (7.31)

Интегрируя (7.31), получаем

, (7.32)

где С₁ – постоянная интегрирования.

Потенцируя (7.32), имеем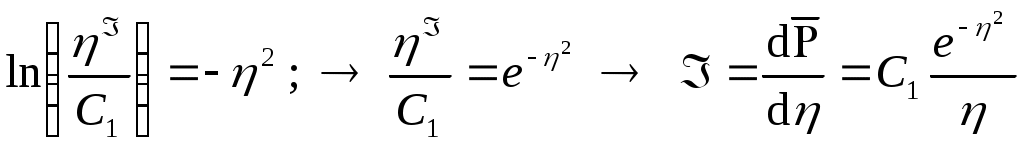

. (7.33)

Интегрируя (7.33) и учитывая первое из условия (7.30), получаем

. (7.34)

Умножая (7.33) на , устремляя  0 и используя второе из условий (7.30), находим

.

Тогда из (7.34) получим

. (7.35)

Интеграл в последней формуле легко свести к табличному следующей подстановкой

.

Тогда .

Перейдем от безразмерного давления 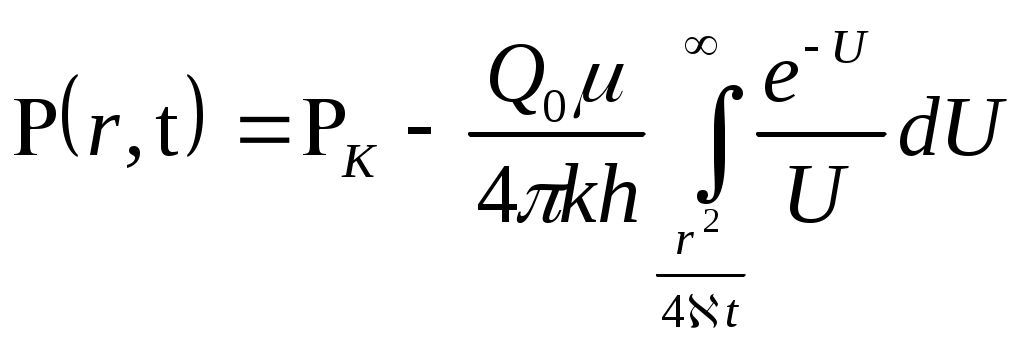к размерному , получим

. (7.36)

Интеграл в (7.36) называется интегральной показательной функцией, которая табулирована и обозначается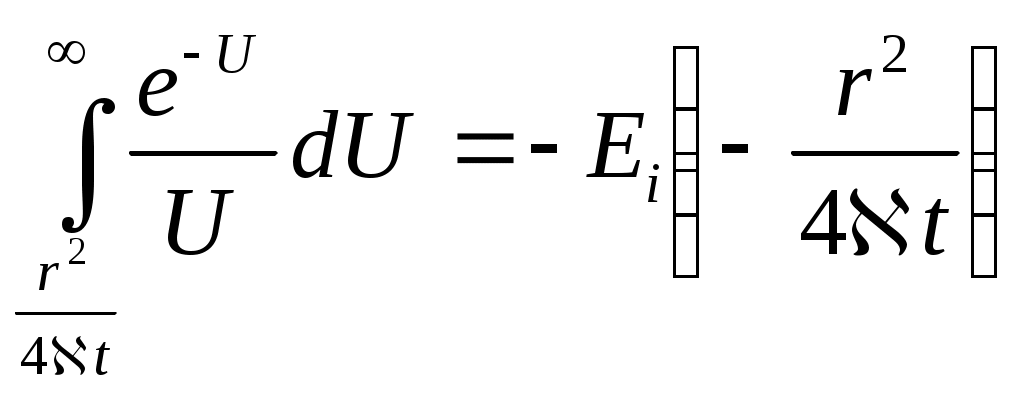

.

К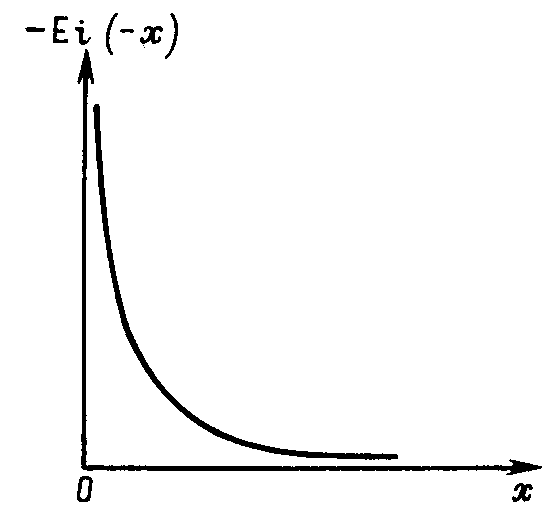
ачественное изменение этой функции показано на рис. 45.

Рис. 45

Следовательно, давление в любой точке плоскорадиального потока в условиях упругого режима фильтрации определяется по формуле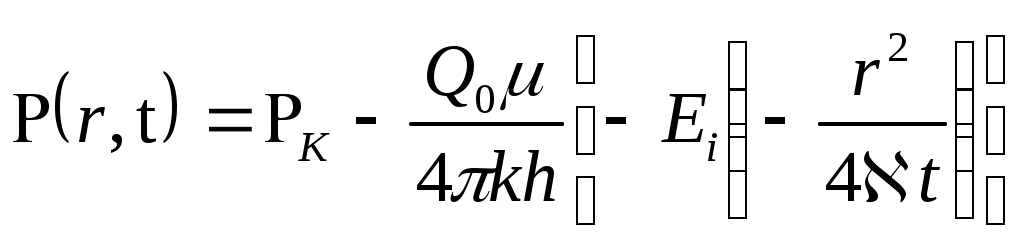

. (7.37)

Формула (7.37) называется основной формулой теории упругого режима фильтрации. Она носит широкое практическое применение, и в частности используется при интерпретации результатов исследования скважин.

При малых значениях аргумента - интегральная показательная функция имеет простую асимптотику:

,

где 0,5772 = ln 1,781 = С_Э – константа Эйлера;

т.е. ; (7.38)

при этом погрешность не превышает

0,25 %, если ;

1,0 % , если .

Таким образом, при малых значениях , т.е. при больших значениях времени t, можно пользоваться приближенной формулой, вытекающей из (7.37) и (7.38)

,

или

. (7.39)

Из (7.37) находим, что расход жидкости через любую цилиндрическую поверхность радиусом r и скорость фильтрации определяются соответственно по формулам

; (7.40)

. (7.41)

Из последней формулы следует, что стационарная скорость достигается очень быстро на небольших расстояниях от скважины, т.к. значение коэффициента пьезопроводности  очень велико.

Заметим, что формула (7.37) справедлива лишь для точечного стока, т.е. для r = 0 в неограниченном пласте (R_K = ).

Для оценки влияния конечного радиуса возмущающей скважины r_C на результаты расчетов давления В.Н.Щелкачев использовал параметр Фурье . С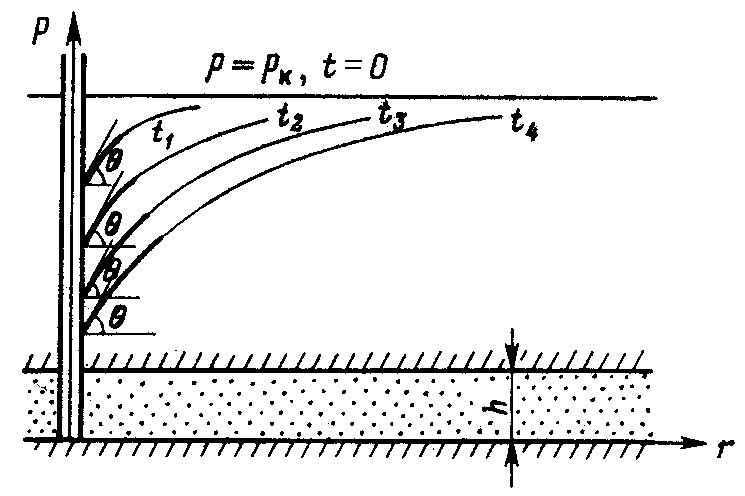равнивая результаты расчетов давления по формуле (7.37) с точными данными Ван-Эвердингера и Херста, учитывающими конечный радиус скважины r_C, В.Н.Щелкачевым было показано, что для скважин обычных размеров формула (7.37) обеспечивает высокую степень точности уже на самой ранней стадии (а тем более на поздней стадии) процесса перераспределения давления.

Р
ассмотрим пьезометрические кривые для бесконечного пласта, который эксплуатируется скважиной радиуса r_C с постоянным дебитом Q₀ (рис.46).

Рис. 46

Для точек вблизи забоя скважины можно пользоваться формулой (7.39); дифференцируя ее по координате r, найдем градиент давления

.

Из этой формулы следует, что градиент давления для значений практически не зависит от времени и определяется по той же формуле, что и для установившейся плоскорадиальной фильтрации несжимаемой жидкости (3.7), (3.9). Для указанных значений r пьезометрические кривые представляют собой логарифмические линии (рис.46), у которых углы наклона  касательных одинаковы для всех кривых у забоя скважины.

Таким образом, вокруг скважины, непрерывно увеличиваясь, образуется область, в пределах которой давление распределяется как при установившемся режиме (область квазиустановившегося процесса) – на рис.46 показаны жирными линиями.

Решение дифференциального уравнения упругого режима для различных случаев фильтрации упругой жидкости в ограниченных открытых и закрытых пластах представляются бесконечными рядами по функциям Бесселя. В то же время непосредственными расчетами В.Н. Щелкачев показал, что в громадном большинстве практически интересных случаев поведение возмущающей скважины в конечном открытом пласте (рис.47) можно в течении достаточно длительного времени изучать при помощи простой формулы (7.37) для бесконечного пласта. В частности расхождение в значениях 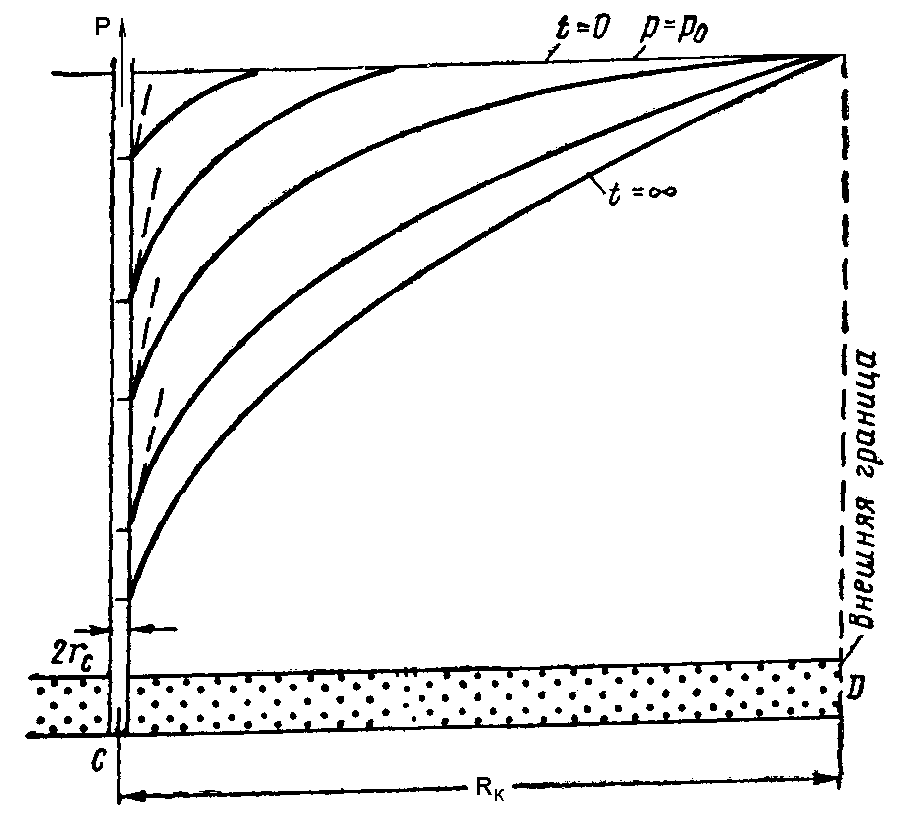для бесконечного и конечного пластов не превосходят 1%, если


и или если

и .

Характер распределения давления Р(r,t) для случаев ограниченного открытого и закрытого пластов показан на рис.47 и 48 соответственно.