Реферат по матметодам. Використання функціїоригіналу для опису фізичного процесу
 Скачать 38.58 Kb. Скачать 38.58 Kb.
|
|
План Основи - використання функції-оригіналу для опису фізичного процесу; - порядок аналізу функції-оригіналу; - формування вимог до функції-образу Використання функції-оригіналу для опису фізичного процесу Функцію-оригінал можна описати так-це будь-яка комплекснозначна функція f(t) дійсного аргументу t яка повинна задовольняти такі умови: f (t) и f '(t) або всюди безперервні, або мають на будь-якому кінцевому проміжку лише кінцеве число точок розриву першого роду; для всіх негативних функцій f (t) = 0, для всіх точок t < 0 ; f (t) зростає не швидше показової функції, тобто існують такі числа M > 0 и s0 ≥ 0, що для всіх t 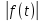 ≤ Mes0t , s0 – показник зростання функції f (t) . ≤ Mes0t , s0 – показник зростання функції f (t) .З точки зору фізичних додатків умови 1 і 3 виконуються для більшості функцій f(t), що описують фізичні процеси (t – час). Умова 2 відповідає умові початку експерименту, тобто вся інформація про хід процесу до моменту початку спостереження міститься в початкових умовах. Математично ця проблема вирішується з використанням одиничної функції Хевісайда η ( t), яка визначається наступним чином: 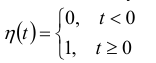 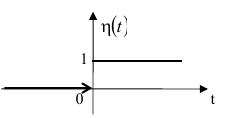 Тоді функцію ϕ (t), яка задовольняє умовам 1 і 3, але не задовольняє умові 2 можна зробити оригіналом, помноживши цю функцію на η(t). ("гасимо" ϕ (t) для значень t < 0 і не змінюємо її для значень t ≥ 0.) 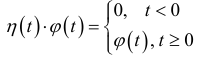 Користуючись одиничною функцією, можна зробити оригіналами такі відомі функції, як sint, cost, cht, sht, eλt . - Порядок аналізу функції-оригіналу; Для початку ми виробляємо графічну побудову просторової фігури робочої або утворює рівняння функції в своєму власному просторі. Аналізуємо конструкцію фігури функції (взаємна віддаленість екстремумів по вертикалі і горизонталі, крутизна схилів); просторове розташування фігури функції; характер і розташування коренів, і т. д. Виводимо загальні вирази для коренів функції-оригіналу, визначаємо їх чисельне значення. Потім аналізуємо залежність сигналів вхід-вихід і інших параметрів моделі від номіналів фізичних елементів, комплектуючих макет. Оцінюємо розташування і можливість переміщення робочої точки і інтервалу регулювання. Оцінюємо стійкість роботи макета і можливість переміщення (коригування положення) робочої точки з метою зміни стану стійкості. - Формування вимог до функції-образу Графічна побудова фігури синтезованої функції з урахуванням вимог до якості і розміщення в просторі. Завдання розміщення робочої точки і інтервалу регулювання на «тілі» функції.. Завдання крутизни і лінійності ділянки регулювання робочої функції Кількісне завдання рівнів стійкості, надійності, економічності та інших якісних характеристик проекту у функції номіналів фізичних елементів, сигналів та інших параметрів моделі, що визначають коефіцієнти функції-образу. Формування вимог до функції синтезованої моделі у формі рівнянь зв'язку між коефіцієнтами функції-образу. Література 1) Операционное исчисление http://imas.tpu.ru/lecture/%D0%BA%D0%BE%D0%BD%D1%81%D0%BF%D0%B5%D0%BA%D1%82%20operation%20calculus.pdf 2) Крайнов А.Ю., Рыжих Ю.Н. Операционное исчисление. Примеры задач. - 2007 https://ftf.tsu.ru/wp-content/uploads/Operatsionnoe-ischislenie-primery-i-zadachi-A.YU.-Krajnov-YU.N.-Ryzhih.pdf 3) Корчагин И.Ф.«АНАЛИТИЧЕСКИЙ СИНТЕЗ И АНАЛИЗ МАТЕМАТИЧЕСКИХ МОДЕЛЕЙ» - 2006 https://www.bezopasnost.ru/upload/iblock/453/korchagin7.pdf
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
