«Вынужденные колебания систем с одной степенью свободы без учета. Вынужденные колебания систем с одной степенью свободы без учета демпфирования
 Скачать 378.79 Kb. Скачать 378.79 Kb.
|
|
Министерство образования и науки Республики Казахстан НАО «Евразийский национальный университет имени Л.Н.Гумилева» Архитектурно-строительный факультет СРО №6 По дисциплине «Динамика и устойчивость сооружений» На тему: «Вынужденные колебания систем с одной степенью свободы без учета демпфирования» Проверил: Абильмаженов Т. Ш. Выполнила: Батурина О.В. Астана 2022 План: 1. Действие мгновенного импульса 2. Действие системы импульсов 3. Действие произвольной нагрузки 4. Действие вибрационной нагрузки 5. Действие внемассовой нагрузки 6. Кинематическое возмущение эпюр 1. Действие мгновенного импульса Пусть находящаяся в покое колебательная система с массой m в момент времени подвергается действию мгновенного импульса S (рис. 2.9 а). Это воздействие вызовет свободные колебания системы, которые, если не учитывать демпфирование, можно считать собственными колебаниями. Поэтому примем 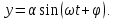 (2.32) (2.32)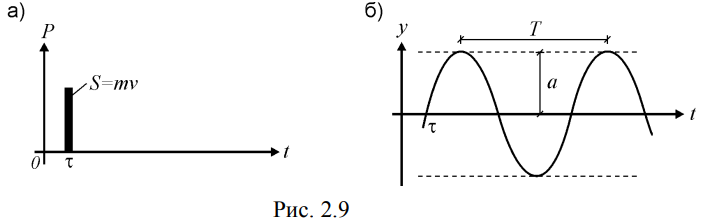 Мгновенный импульс не успевает изменить положение массы, поэтому yt= 0. Однако, действуя как импульс, он сообщает массе начальную скорость vt=S/m. По этим начальным условиям из (2.32) определим амплитуду и начальную фазу колебаний: a = S /m , = – . Тогда уравнение (2.32) принимает вид 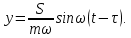 (2.33) (2.33)Значит, колебания массы m будут происходить с собственной частотой и периодом T собственных колебаний системы. График этого движения представлен на рис. 2.9 б. 2. Действие системы импульсов Если в моменты 1,2,…,k на систему действуют несколько мгновенных импульсов S1, S2, ..., Sk, то на основе принципа суперпозиции (независимости действия сил), перемещение массы будет определяться суммой перемещений от каждого импульса. С учетом (2.33), получим Наиболее невыгодным, оказывающим наибольшее воздействие на систему, является периодическое действие импульсов. Пусть импульсы равной величины S действуют через период Ts (рис. 2.10 а). Если момент (время) начала действия первого импульса принять 1=0, то момент приложения i-го импульса будет i=(i–1)Ts . Тогда имеем 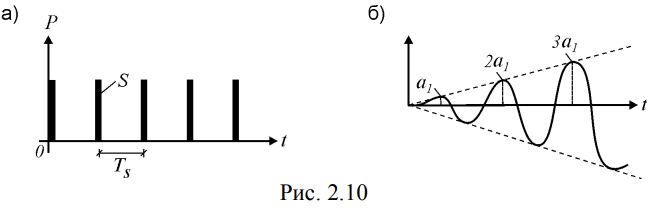 Если период действия импульсов равен периоду собственных колебаний (т.е. Ts=T=2 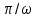 ), то уравнение движения массы будет определяться формулой ), то уравнение движения массы будет определяться формулой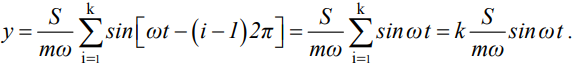 Из него следует, что амплитуда колебаний зависит от числа импульсов k: График этого движения представлен на рис. 2.10 б. Таким образом, при действии импульсов с постоянной частотой, равной частоте собственных колебаний системы, амплитуда колебаний равномерно и неограниченно растет. Совпадение частоты возмущающей силы с собственной частотой и сопровождающие его явления называются резонансом. При резонансных колебаниях сооружения возникают большие деформации и напряжения, что может привести к разрушениям. 3. Действие произвольной нагрузки Для определения частного решения неоднородного дифференциального уравнения Он называется интегралом Дюамеля.  Так как это есть частное решение дифференциального уравнения (2.29), а общее решение однородного уравнения определяется по формуле (2.31), то общее решение всего уравнения будет 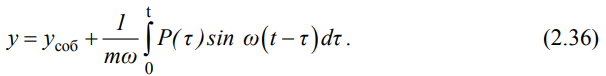 Первое слагаемое yсоб в этом выражении соответствует собственным колебаниям системы, а второе − вынужденным колебаниям. Таким образом, масса совершает сложное движение, состоящее из суммы двух колебаний. Однако, из-за наличия внутреннего трения (в реальных системах − сооружениях − оно всегда присутствует) свободные колебания затухают. Поэтому через некоторое время после начала колебаний свободными колебаниями можно пренебречь и считать, что в дальнейшем система совершает только чисто вынужденные колебания, определяемые выражением (2.35). 4. Действие вибрационной нагрузки Рассмотрим вибрационную нагрузку, изменяющуюся по закону P(t)=P0sin θt. Если подставить эту функцию в (2.35), получим выражение 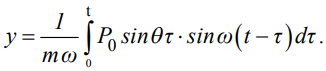 Его интегрирование дает следующий результат Первое слагаемое в правой части этой формулы sinωt соответствует собственным колебаниям с частотой , а второе слагаемое представляет чисто вынужденные колебания с частотой вибрационной силы θ. В обычных сооружениях собственные колебания быстро затухают и после нескольких колебаний остаются лишь вынужденные колебания. Этот процесс называется установлением колебаний. После установления колебаний система колеблется лишь с частотой возмущающей силы: Преобразуем эту формулу. Так как Здесь P0 = yст − статический прогиб под действием силы P0. Тогда По этой формуле можно заключить, что, в зависимости от частоты, вибрационная нагрузка может оказывать бόльшее воздействие чем статическая нагрузка. С целью изучения этого явления вводится понятие коэффициента динамичности , который показывает, во сколько раз максимальное отклонение от динамической нагрузки больше отклонения от ее статического действия:  Если этот коэффициент известен, то расчет на динамическую нагрузку P(t)=P0sint можно заменить расчетом на статическую нагрузку P= P0 . Коэффициент динамичности вибрационной силы определяется из (2.39): Эта формула используется при малых частотах вибрационной силы, когда θ. При больших частотах, когда θ, получаем Значит, в этом случае Анализ формулы (2.38) позволяет сделать некоторые выводы: 1) когда θ, знак отклонения y совпадает со знаком силы P, поэтому вибрационная сила и вызванное ею перемещение массы находятся в одной фазе; 2) когда θ, то знак отклонения будет противоположен знаку силы, т.е. возмущающая сила P и перемещение y будут в противофазе; 3) когда частота вынуждающей силы приближается к частоте собственных колебаний, т.е. θ , то амплитуда колебаний неограниченно возрастает: y ∞. Такой случай соответствует резонансу. Однако, вывод о неограниченном возрастании перемещений был получен без учета затухания колебаний. В действительности, из-за наличия демпфирования, этого не будет. Этот вывод не справедлив и потому, что в области больших деформаций становится непригодным решение теории линейных колебаний. Поэтому резонанс следует рассматривать как случай, когда значительно возрастает амплитуда колебаний (рис. 2.12). И это может стать опасным для прочности Рис. 2.12 сооружения. 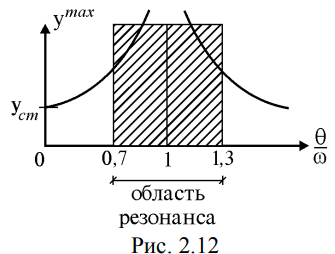 Согласно нормам, в период установившегося режима работы машин нужно стремиться к тому, чтобы частоты θ и отличались друг от друга не менее чем на 30%, т.е. чтобы их отношение не лежало в интервале 5. Действие внемассовой нагрузки Приложение динамической нагрузки в системе вне массы (рис. 2.13 а) является более общим случаем рассмотренного вопроса. Такая задача решается путем замены действующей внемассовой силы P(t) на эквивалентную ей заменяющую силу Pm(t) (рис. 2.13 б). Заменяющая сила Pm(t) должна дать такое же перемещение массы m, что и сила P(t), т.е. должно быть y(t)=ym(t). С другой стороны, ym(t)=Pm(t) , где – податливость балки в точке расположения массы m (рис. 2.13 в). Тогда внемассовая нагрузка приводится к замещающей силе. 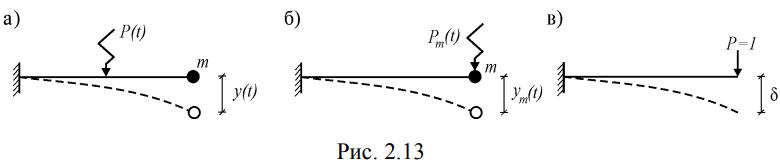 6. Кинематическое возмущение эпюр Рассмотрим балку с массой m (рис. 2.14 а), правая опора которой перемещается по известному закону (t). 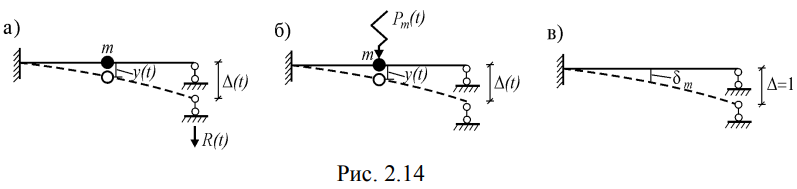 Условно можно считать, что балка совершает вынужденные колебания под действием реакции R(t) в опоре при ее смещении на (t). Тогда, на основании формулы (2.44), внемассовую силу R(t) можно заменить силой приложенной к массе (рис. 2.14 б). Перемещение y(t) найдем по методу перемещений, рассматривая единичное состояние балки (рис. 2.14 в) при =1. Если m – перемещение массы m, то Тогда заменяющая сила, эквивалентная смещению (t), будет Подставляя ее в (2.36), получим 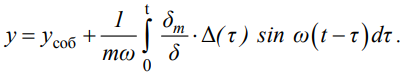 С учетом того, что 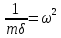 , окончательно получаем , окончательно получаем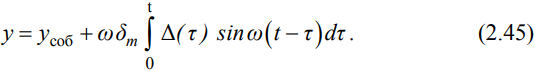 Рассмотрим частный случай кинематического возбуждения по гармоническому закону где Δ0 – амплитудное значение смещения опоры, θ – частота кинематического возбуждения. Подставляя (2.46) в (2.45), имеем 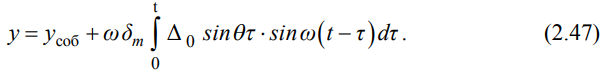 После интегрирования и ряда преобразований получим 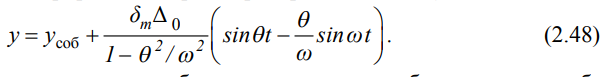 При длительных колебаниях влиянием собственных колебаний (перемещением yсоб и вторым слагаемым в скобках) можно пренебречь. Тогда перемещение массы и действующая на нее инерционная сила будут 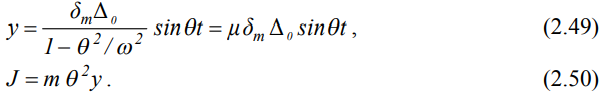 Список использованной литературы: 1. Динамика и устойчивость сооружений Р.А. Шакирзянов, Ф.Р. Шакирзянов, Казань Ай Пи Ар Медиа, 2022, 119 стр. 2. Динамика и устойчивость сооружений: учеб. пособие / А. К. Рябухин, Д. В. Лейер, Н. Н. Любарский. – Краснодар: КубГАУ, 2020. – 171 с. |
