Выполнение и анализ простых алгоритмов

• Название: Выполнение и анализ простых алгоритмов
• Дата: 18.06.2022
• Размер: 190.3 Kb.
• Имя файла: ege5.docx
• Тип: Документы; #601056
• страница: 3 из 13

Пример задания:

Р-10. Автомат получает на вход натуральное число X. По этому числу строится трёхзначное число Y по следующим правилам.

1. Первая цифра числа Y (разряд сотен) – остаток от деления X на 2.

2. Вторая цифра числа Y (разряд десятков) – остаток от деления X на 3.

3. Третья цифра числа Y (разряд единиц) – остаток от деления X на 5.

Пример. Исходное число: 55. Остаток от деления на 2 равен 1; остаток от деления на 3 равен 1; остаток от деления на 5 равен 0. Результат работы автомата: 110.

Укажите наименьшее двузначное число, при обработке которого автомат выдаёт результат 104.

Решение (метод подбора, П.Е. Финкель, г. Тимашевск):

1. 
   обозначим искомое число через N
   
2. 
   остаток от деления на 2, равный 1, говорит о том, что число нечётное
   
3. 
   таким образом, нужно найти нечётное число, которое делится на 3 и при делении на 5 даёт остаток 4
   
4. 
   перебираем нечётные двузначные числа, которые при делении на 5 дают остаток 4 и находим для каждого остаток от деления на 3:
   

   N	19	29	39	…
   N mod 3	1	2	0

5. 
   Ответ: 39.
   

Решение (использование уравнений):

1. 
   обозначим искомое число через N
   
2. 
   если остаток от деления числа N на число d равен r, то справедливо равенство
   

N = dk + r,

где k – целое число

3. 
   тогда из п. 1-3 условия получаем
   

1. N = 2 k + 1 (N – нечётное)

2. N = 3m,

3. N = 5q + 4,

где k, m, q – целые числа

4. 
   наибольшие ограничения накладывает последнее условие (заданный остаток от деления на наибольшее число), поэтому начнём с него
   
5. 
   объединим второе условие с третьим:
   

N = 3m = 5q + 4,

Мы получили диофантово уравнение в целых числах, оно имеет бесконечно много решений. Найдём перебором одно из решений, а потом, если оно не подошло, будем перебирать остальные, пока не решим задачу.

6. 
   из написанного выше уравнения имеем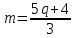
   

7. 
   мы должны получить целое m, используем метод перебора: подставляем в эту формулу разные значения q = 0, 1, 2, … до тех пор, пока не получится целое m; это случится при q = 1, тогда m = 3 и N = 9, но это однозначное число (не подходит по условию, нужно двузначное)
   
8. 
   продолжаем перебор: поскольку нужно сохранить делимость на 3, далее проверяем значения q = 1+3, 1+23, 1+33 и т.д
   
9. 
   при q = 4 получаем m = 8 и N = 24, но это чётное число (не выполняется условие 1)
   
10. 
    при q = 7 получаем m = 13 и N = 39, это число двузначное и нечётное, это и есть ответ
    
11. 
    Ответ: 39.
    

Ещё пример задания:

Р-09. Автомат получает на вход четырёхзначное натуральное число и строит новое число по следующему алгоритму:

1. 
   вычисляются суммы первой и второй, второй и третьей и третьей и четвёртой цифр;
   
2. 
   из полученных сумм отбрасывается наименьшая;
   
3. 
   остальные записываются в порядке неубывания.
   

Пример. Исходное число:1284. Суммы: 1 + 2 = 3; 2 + 8 = 10; 8 + 4 = 12. Отбрасывается наименьшая сумма 3. Результат: 1012. Укажите наименьшее и наибольшее число, при вводе которого автомат выдаёт значение 511.

Решение:

1. 
   число 511 разбивается на две суммы, расположенные в порядке неубывания (возрастания) однозначно – 5 и 11
   
2. 
   сначала определим наименьшее возможное число; для этого все цифры с больши́ми значениями нужно «загонять» в конец числа, а все маленькие – в начало
   
3. 
   первая сумма должна быть наименьшей – она будет отброшена
   
4. 
   наименьшая возможная первая цифра – 1 (0 выбирать нельзя, иначе число не будет 4-значным); число принимает вид 10**, где * обозначает ещё не определённую цифру
   
5. 
   второй цифрой можно выбрать наименьшую возможную – 0, при этом сумму второй и третьей можно сделать равной 5, выбрав третью цифру 5; число соответствует шаблону 105*
   
6. 
   сумма двух последних цифр должна быть равна 11, поэтому последняя цифра = 11 – 5 = 6
   
7. 
   Ответ: минимальное число – 1056.
   
8. 
   теперь построим наибольшее число: все «большие» суммы и, соответственно, «большие» цифры сдвигаем влево, к началу числа
   
9. 
   сначала получим сумму 11 из первых двух цифр; наибольшее число получится, если выбрать старшую цифру 9, а вторую 11 – 9 = 2; получаем число 92**
   
10. 
    вторая сумма должна быть равна 5, поэтому третья цифра 5 – 2 = 3, получаем 923*
    
11. 
    последнюю сумму нужно сделать не больше, чем 5 (она будет отброшена), поэтому наибольшее число получается при последней цифре 2 (последняя сумма равна 5)
    
12. 
    Ответ: максимальное число – 9232.