фигня. Выполнение и анализ простых алгоритмов

• Название: Выполнение и анализ простых алгоритмов
• Анкор: фигня
• Дата: 21.02.2022
• Размер: 0.66 Mb.
• Имя файла: ege5.doc
• Тип: Документы; #369032
• страница: 1 из 12

© К. Поляков, 2009-2021

5 (базовый уровень, время – 4 мин)

Тема: Выполнение и анализ простых алгоритмов.

Что проверяется:

Формальное исполнение алгоритма, записанного на естественном языке, или умение создавать линейный алгоритм для формального исполнителя с ограниченным набором команд.

1.6.3. Построение алгоритмов и практические вычисления.

1.1.3. Умение строить информационные модели объектов, систем и процессов в виде алгоритмов.

Что нужно знать:

• 
  сумма двух цифр в десятичной системе счисления находится в диапазоне от 0 до 18 (9+9)
  
• 
  в некоторых задачах нужно иметь представление о системах счисления (могут использоваться цифры восьмеричной и шестнадцатеричной систем счисления)
  
• 
  бит чётности – это дополнительный контрольный бит, который добавляется к двоичному коду так, чтобы количество единиц в полученном двоичном коде стало чётным; если в исходном коде уже было чётное количество единиц, дописывается 0, если нечётное – дописывается 1.
  
• 
  при добавлении к двоичной записи числа нуля справа число увеличивается в 2 раза
  
• 
  чтобы отбросить последнюю цифру в двоичной записи, нужно разделить число на 2 нацело (остаток отбрасывается)
  

Пример задания:

Р-13 (демо-2021). На вход алгоритма подаётся натуральное число N. Алгоритм строит по нему новое число R следующим образом.

1. Строится двоичная запись числа N.

2. К этой записи дописываются справа ещё два разряда по следующему правилу:

а) складываются все цифры двоичной записи числа N, и остаток от деления суммы на 2 дописывается в конец числа (справа). Например, запись 11100 преобразуется в запись 111001;

б) над этой записью производятся те же действия – справа дописывается остаток от деления суммы её цифр на 2.

Полученная таким образом запись (в ней на два разряда больше, чем в записи исходного числа N) является двоичной записью искомого числа R. Укажите такое наименьшее число N, для которого результат работы данного алгоритма больше числа 77. В ответе это число запишите в десятичной системе счисления.

Решение:

1. 
   фактически на шаге 2а добавляется бит чётности так, чтобы количество единиц в двоичной записи нового числа стало чётным;
   
2. 
   на шаге 2б всегда дописывается 0, поскольку после шага 2а число единиц уже чётно;
   
3. 
   если двоичная запись числа оканчивается на 0, то число чётно, поэтому имеет смысл искать число-результат R среди чётных чисел
   
4. 
   возьмём первое чётное число, большее, чем 77, и переведём его в двоичную систему:
   78 = 1001110₂ ; во время компьютерного ЕГЭ вы можете использовать программистский (или инженерный, до Windows 7 ) режим калькулятора или команду bin(78) интерпретатора Python)
   
5. 
   видим, что все условия выполняются: в двоичной записи числа 78 чётное число единиц (четыре), поэтому оно могло быть получено в результате работы приведённого алгоритма
   
6. 
   во время работы алгоритма к двоичной записи приписали сзади две цифры, их нужно отбросить (в консоли Python можно ввести 78>>2 или 78//4), получается 10011₂ = 19
   
7. 
   Ответ: 19.
   

Решение (теоретическое, И.В. Степанов):

1. 
   дописывание справа к числу 0 или 1 по сути сдвигает побитово число влево; в некоторых случаях может добавиться 1;
   
2. 
   это значит, что после действия 2а либо 2N, либо 2N+1
   
3. 
   операция всегда удваивает число, то есть после операций 2а и 2б мы получим либо 4N, либо 2(2N + 1) = 4N + 2
   
4. 
   таким образом, мы можем взять число 77+1 и просто поделить его на 4: 78 / 4= 19,5
   
5. 
   рассмотрим ближайшие числа; число 18 слишком мало
   
6. 
   далее можно перебирать 19, 20, 21 ... выполняя алгоритм; на числе 19 получим искомый результат
   
7. 
   Ответ: 19.
   

Решение (с помощью Калькулятора Windows, Б.С. Михлин):

1. 
   переключаем Калькулятор в режим Программист (Вид – Программист или Alt+3);
   
2. 
   в десятичной системе (по умолчанию включен режим Dec) набираем 78;
   
3. 
   под окошком вывода отображается двоичный код 78 (0…01001110);
   
4. 
   т.к. двоичный код содержит четное количество единиц (четыре), то R может равняться 78.
   
5. 
   чтобы получить ответ (N) надо от двоичного кода R=78 отбросить два правых разряда. Для этого можно использовать команду Калькулятора сдвиг вправо (Right SHift): нажать кнопку Rsh, затем кнопку «2» (сдвиг на два разряда) и кнопку «=»;
   
6. 
   в окошке вывода видим ответ в десятичном коде: 19
   
7. 
   Ответ: 19.
   

Решение с помощью программы:

1. 
   данное задание проще решить на бумажке, но при желании (и наличии времени) можно проверить с помощью программы
   
2. 
   нам нужно перебирать чётные числа, большие 77, и остановиться, когда найдено число-результат, которое мог получить автомат; основная программа представляет собой цикл с условием:
   

R = 78

while not OK( R ):

R += 2

Здесь функция OK(R) (мы напишем ёё дальше) возвращает «истину» (True), если число R удовлетворяет условиям. Таким образом, цикл заканчивается, когда найдено подходящее значение R.

3. 
   при выводе после завершения цикла мы отбрасываем две последние цифры в двоичной записи, это можно сделать, разделив число нацело на 4:
   

print( R // 4 )

4. 
   функция OK(R) должна вернуть True, если в двоичной записи числа чётное количество единиц (последний 0 будет всегда, так как мы перебираем только чётные числа!):
   

def OK( R ):

s = bin(R)[2:]

return s.count('1') % 2 == 0

С помощью встроенной функции bin строим двоичную запись числа, срезом [2:] убираем символы "0b" в начале. Затем считаем число символов '1' с помощью метода count и проверяем полученное значение на чётность.

5. 
   приведём полную программу
   

def OK( R ):

s = bin(R)[2:]

return s.count('1') % 2 == 0
R = 78

while not OK( R ):

R += 2

print( R // 4 )

6. 
   (А. Сидоров) вместо целочисленного деления на 4 можно использовать битовый сдвиг вправо на 2 позиции:
   

print( R >> 2 )

7. 
   (Б.С. Михлин) Когда мы считаем количество единиц в двоичном коде, то префикс 0b никак не повлияет на результат. Поэтому срез можно не использовать (s = bin(x)[2:]).
   
8. 
   если не использовать функцию (OK), то программу можно немного сократить:
   

R = 78

while True:

if bin(R).count('1') % 2 == 0:

print( R//4 )

break

R += 2

Решение с помощью программы (П.Е. Финкель, г. Тимашевск):

1. 
   часто бывает проще использовать перебор, в котором реализован алгоритм, описанный в задании:
   

1. 
   Число R > 77, рассматриваем числа N на отрезке (1, 70)
   
2. 
   Переводим число n в двоичную систему
   
3. 
   Считаем количество единиц
   
4. 
   Два раза добавляем остаток от деления k на два (либо 0, либо 1)
   
5. 
   Переводим в десятичную систему
   
6. 
   Если R >77 выводим число N; можно поставить break, чтобы не выводить остальные.
   

2. 
   полная программа:
   

for n in range(1,70):

s = bin(n)[2:]

k = s.count("1")

s += str(k%2)

k = s.count("1")

s += str(k%2)

r = int(s,2)

if r > 77:

print(n)

break

3. 
   вариант на языке Pascal (используется модуль school):
   

uses school;

var n,i,k,a,b,c: integer;

s: string;

begin

for n:= 1 to 70 do begin

s:= bin(n);

k:= 0;

for i:=1 to s.Length do

k += StrToInt(s[i]);

s+= k mod 2;

k:= 0;

for i:=1 to s.Length do

k += StrToInt(s[i]);

s+= k mod 2;

c:= dec(s,2);

if c > 77 then begin

println(n);

break

end;

end;

end.

4. 
   Ответ: 19.
   

Решение с помощью программы (М. Коротков):

1. 
   программа на С++, моделирующая работу автомата (перебор):
   

#include

#include
using namespace std;
int main() {

int N = 0;

bitset<32> R;

do {

N++;

R = bitset<32>(N);

for (int i = 1; i <= 2; i++) {

R <<= 1;

R[0] = R.count() % 2;

}

} while (R.to_ulong() <= 77);
cout << N << endl;
return 0;

}

2. 
   Ответ: 19.
   

Решение с помощью электронных таблиц (Б.С. Михлин):

1. 
   в электронных таблицах есть целый набор встроенных функций для перевода целых чисел из одной системы счисления в другую; если десятичное число не превосходит 511 (от -512 до 511), то для перевода его из десятичной в двоичную систему можно воспользоваться функцией: ДЕС.В.ДВ в Excel и Calc Libre Office или DEC2BIN в Calc OpenOffice (вExcel эти формулы находятся в группе Другие функции – Инженерные, в LibreOffice– в меню Вставка – Функция … – Категория: Подключаемый модуль, в OpenOffice – в меню Вставка – Функция … – Категория: Дополнение)
   
2. 
   в современных версиях электронных таблиц (например, в Excel 2013 и более поздних) добавлена более мощная и универсальная функция:
   

ОСНОВАНИЕ в Excel и Calc Libre Office или BASE в Calc Open Office

она позволяет переводить целые неотрицательные числа практически не ограниченной величины (меньше 2⁵³) в любую систему счисления (с основанием от 2 до 36)

3. 
   Решение в Excel выглядит так: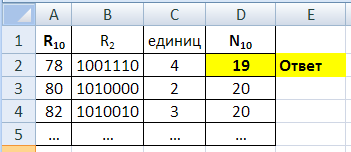
   

А вот так выглядят формулы: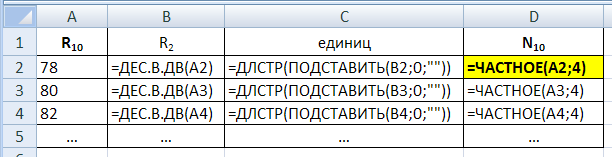

4. 
   в столбце А записываются числа-кандидаты (чётные числа, большие 77)
   
5. 
   в столбце B для каждого такого числа строится двоичная запись с помощью функции ДЕС.В.ДВ (английский вариант DEC2BIN)
   
6. 
   в столбце С с помощью функции ПОДСТАВИТЬ (SUBSTITUTE) удаляем все нули, заменяя их на пустые строки, и считаем количество оставшихся единиц
   
7. 
   в столбце D с помощью функции ЧАСТНОЕ (QUOTIENT) делим исходное число на 4, отбрасывая остаток
   
8. 
   в OpenOffice формулы с английскими названиями функций выглядят так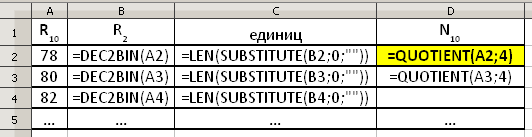
   

9. 
   Ответ: 19.
   
10. 
    (К. Поляков) «для красоты» можно убрать все значения, которые не подходят, то есть содержат в двоичном представлении нечётное количество единиц: