Практическая работа №3 математика. Выполнение практической работы 3 Анализ содержания и методического аппарата умк с точки зрения требований примерных рабочих программ по математике
 Скачать 118.21 Kb. Скачать 118.21 Kb.
|
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| УМК ,предмет, класс УМК Виленкин Н.Я. математика 5 класс | Содержание учебного материала | |
| Наличие элементов содержания согласно ПРП - отметить знаком «+» | Отсутствующие элементы содержания согласно ПРП – отметить знаком «-» | |
| Натуральное число, множество натуральных чисел и его свойства, изображение натуральных чисел точками на числовой прямой. | Натуральное число. Ряд натуральных чисел. Число 0. Изображение натуральных чисел точками на координатной (числовой) прямой. | |
| Обозначение натуральных чисел. Различие между цифрой и числом. Позиционная запись натурального числа, поместное значение цифры, разряды и классы, соотношение между двумя соседними разрядными единицами, чтение и запись натуральных чисел. | Позиционная система счисления. Римская нумерация как пример непозиционной системы счисления. Десятичная система счисления. | Позиционная система счисления. Римская нумерация как пример непозиционной системы счисления. Десятичная система счисления. |
| Сравнение натуральных чисел, сравнение с числом Понятие о сравнении чисел, сравнение натуральных чисел друг с другом и с нулём, математическая запись сравнений, способы сравнения чисел. | Сравнение натуральных чисел, сравнение натуральных чисел с нулём. Способы сравнения. Округление натуральных чисел. | |
| Действия с натуральными числами Сложение и вычитание, компоненты сложения и вычитания, связь между ними, нахождение суммы и разности, изменение суммы и разности при изменении компонентов сложения и вычитания. Умножение и деление, компоненты умножения и деления, связь между ними, умножение и сложение в столбик, деление уголком, проверка результата с помощью прикидки и обратного действия. Переместительный и сочетательный законы сложения и умножения, распределительный закон умножения относительно сложения, обоснование алгоритмов выполнения арифметических действий. | Сложение натуральных чисел; свойство нуля при сложении. Вычитание как действие, обратное сложению. Умножение натуральных чисел; свойства нуля и единицы при умножении. Деление как действие, обратное умножению. Компоненты действий, связь между ними. Проверка результата арифметического действия. Переместительное и сочетательное свойства (законы) сложения и умножения, распределительное свойство (закон) умножения. | |
| Использование букв для обозначения чисел, вычисление значения алгебраического выражения, применение алгебраических выражений для записи свойств арифметических действий, преобразование алгебраических выражений. | Использование букв для обозначения неизвестного компонента и записи свойств арифметических действий. | |
| Деление с остатком на множестве натуральных чисел, свойства деления с остатком. Практические задачи на деление с остатком. | Делители и кратные числа, разложение на множители. Простые и составные числа. Признаки делимости на 2, 5, 10, 3, 9. Деление с остатком. | Делители и кратные числа, разложение на множители. Простые и составные числа. Признаки делимости на 2, 5, 10, 3, 9. Деление с остатком. |
| Степень с натуральным показателем Запись числа в виде суммы разрядных слагаемых, порядок выполнения действий в выражениях, содержащих степень, вычисление значений выражений, содержащих степень. | Степень с натуральным показателем. Запись числа в виде суммы разрядных слагаемых. | |
| Числовые выражения Числовое выражение и его значение, порядок выполнения действий. | Числовое выражение. Вычисление значений числовых выражений; порядок выполнения действий. Использование при вычислениях переместительного и сочетательного свойств (законов) сложения и умножения, распределительного свойства умножения. | |
| Доля, часть, дробное число, дробь. Дробное число как результат деления. Правильные и неправильные дроби, смешанная дробь (смешанное число). Преобразование смешанной дроби в неправильную дробь и наоборот. Сравнение обыкновенных дробей. | Представление о дроби как способе записи части величины. Обыкновенные дроби. Правильные и неправильные дроби. Смешанная дробь; представление смешанной дроби в виде неправильной дроби и выделение целой части числа из неправильной дроби. Изображение дробей точками на числовой прямой. Основное свойство дроби. Сокращение дробей. Приведение дроби к новому знаменателю. Сравнение дробей | Основное свойство дроби. Сокращение дробей. Приведение дроби к новому знаменателю |
| Сложение и вычитание обыкновенных дробей. Деление и дроби. Сложение и вычитание смешанных чисел. | Сложение и вычитание дробей. Умножение и деление дробей; взаимно-обратные дроби. Нахождение части целого и целого по его части. | Умножение и деление дробей; взаимно-обратные дроби. Нахождение части целого и целого по его части. |
| Целая и дробная части десятичной дроби. Преобразование десятичных дробей в обыкновенные. Сравнение десятичных дробей. | Десятичная запись дробей. Представление десятичной дроби в виде обыкновенной. Изображение десятичных дробей точками на числовой прямой. Сравнение десятичных дробей. | |
| Сложение и вычитание десятичных дробей. Округление десятичных дробей. Умножение и деление десятичных дробей | Арифметические действия с десятичными дробями. Округление десятичных дробей. | |
| Решение текстовых задач арифметическим способом. Использование таблиц, схем, чертежей, других средств представления данных при решении задачи. | Решение текстовых задач Решение текстовых задач арифметическим способом. Решение логических задач. Решение задач перебором всех возможных вариантов. Использование при решении задач таблиц и схем. | |
| Единицы измерений: длины, площади, объёма, массы, времени, скорости. Зависимости между единицами измерения каждой величины. Зависимости между величинами: скорость, время, расстояние; производительность, время, работа; цена, количество, стоимость. | Решение задач, содержащих зависимости, связывающие величины: скорость, время, расстояние; цена, количество, стоимость. Единицы измерения: массы, объёма, цены; расстояния, времени, скорости. Связь между единицами измерения каждой величины. | |
| Решение задач на нахождение части числа и числа по его части. Решение задач на проценты и доли. Решение несложных задач на движение в противоположных направлениях, в одном направлении, движение по реке по течению и против течения. Применение дробей при решении задач. | Решение основных задач на дроби. | |
| Столбчатые и круговые диаграммы. Извлечение информации из диаграмм. Изображение диаграмм по числовым данным. | Представление данных в виде таблиц, столбчатых диаграмм. | |
| Фигуры в окружающем мире. Наглядные представления о фигурах на плоскости: прямая, отрезок, луч, угол, ломаная, многоугольник, окружность, круг. | Наглядные представления о фигурах на плоскости: точка, прямая, отрезок, луч, угол, ломаная, многоугольник, окружность, круг. Угол. Прямой, острый, тупой и развёрнутый углы. | |
| Четырехугольник, прямоугольник, квадрат. Треугольник. Изображение основных геометрических фигур. Длина отрезка. Единицы измерения длины. Построение отрезка заданной длины. Виды углов. Градусная мера угла. Измерение и построение углов с помощью транспортира. | Длина отрезка, метрические единицы длины. Длина ломаной, периметр многоугольника. Измерение и построение углов с помощью транспортира. | |
| Решение практических задач с применением простейших свойств фигур. | Наглядные представления о фигурах на плоскости: многоугольник; прямоугольник, квадрат; треугольник, о равенстве фигур. | Наглядные представления о фигурах на плоскости: многоугольник; прямоугольник, квадрат; треугольник, о равенстве фигур. |
| Периметр многоугольника. | Изображение фигур, в том числе на клетчатой бумаге. Построение конфигураций из частей прямой, окружности на нелинованной и клетчатой бумаге. Использование свойств сторон и углов прямоугольника, квадрата | Построение конфигураций из частей прямой, окружности на нелинованной и клетчатой бумаге. Использование свойств сторон и углов прямоугольника, квадрата. |
| Понятие площади фигуры; единицы измерения площади. Площадь прямоугольника, квадрата. Приближенное измерение площади фигур на клетчатой бумаге. | Площадь прямоугольника и многоугольников, составленных из прямоугольников, в том числе фигур, изображённых на клетчатой бумаге. Единицы измерения площади. | |
| Наглядные представления о пространственных фигурах: куб, параллелепипед. Изображение пространственных фигур. | Наглядные представления о пространственных фигурах: прямоугольный параллелепипед, куб, многогранники. Изображение простейших многогранников. Развёртки куба и параллелепипеда. Создание моделей многогранников (из бумаги, проволоки, пластилина и др.). | Создание моделей многогранников (из бумаги, проволоки, пластилина и др.). |
| Объём прямоугольного параллелепипеда, куба. Единицы измерения объёма. | Понятие объема; единицы объема. Объем прямоугольного параллелепипеда, куба | |
Заключение : содержание учебных материалов и методического аппарата УМК Виленкина Н.Я. 5 класса соответствуют требованию ПРП основного общего образования частично.
Задание 2. Анализ учебных заданий (методического аппарата УМК) по выбранной теме, распределение учебных заданий по видам формируемых метапредметных результатов. Виленкин Н.Я. Математика – 5 класс Тема
РегулятивныеI. Целеполагание.
Задача №1. Реши задачу.
Печенье упаковали в пачки по 250 г. Пачки сложили в ящик в 4 слоя. Каждый слой имеет 5 рядов по 6 пачек в каждом. Выдержит ли ящик, если максимальная масса, на которую он рассчитан, равна 32 кг?
Решение:
1) 6*5=30 (пачек) в 1 слое
2) 30 * 4=120(пачек) всего в ящике
3) 120*250=30000 (г)=30 (кг) масса всего печенья, что меньше максимальной массы, на которую рассчитан ящик.
Ответ: ящик выдержит.
Комментарий. Проверяется способность сопоставлять полученный результат и поставленный вопрос. В ответе должно быть указано, что ящик выдержит. Ответ о массе всего печенья считается неверным.
Задача №2.
Реши задачу. В кинотеатре два зрительных зала: красный и синий. В красном зале 40 рядов, по 45 мест в каждом. В синем зале 25 рядов, по 24 места в каждом. Во сколько раз число мест в красном зале больше, чем число мест в синем зале?
Комментарий. Проверяется способность "удерживать" цель деятельности в ходе решения учебной задачи: ученик должен выполнить 3 арифметических действия.
Решение
40*45= 1800 (мест) в красном зале
25*24= 600 (мест) в синем зале
1800:600=3 (раза)
Ответ: в 3 раза число мест в красном зале больше, чем число мест в синем зале.
Задача №3. Вычислите значение выражения рациональным способом.
3189 - (1189 + 1250)
Комментарий. Проверяется способность выбирать рациональный способ при решении заданий.
Решение
3189 - (1189 + 1250) = 3189 - 1189 - 1250 =750
Задача №4. Из пунктов А и В навстречу друг другу выехали автомобиль со скоростью 60 км/ч и велосипедист со скоростью 15 км/ч. Встретятся ли они через 2 часа, если расстояние между пунктами 160 км?
Комментарий. Проверяется способность сопоставлять полученный результат и поставленный вопрос. В ответе должно быть указано, что не встретятся. Ответ о том, сколько километров проедут автомобиль и велосипедист за два часа вместе считается неверным.
Решение
60+15=75 (км/ч) - скорость сближения
75*2= 150 (км) - проедут вместе автомобиль и велосипедист за 2 часа. Так как расстояние между пунктами 160км, что не равно пройденному расстоянию, то они не встретятся.
Ответ: не встретятся.
II. Планирование, контроль и оценка учебных действий.
Задача № 1.
При выполнении задания ученик допустил две ошибки.
Отметь верные решения +.
1020 м= 1км 200 м
530см = 5м 3 см
10 км 800 м = 10800 м
30 м 7 см = 370 см
25 км 40 м = 25040 м
Решение:
1020 м= 1км 200 м
530 см = 5м 30 см +
10 км 800 м = 10800 м +
30 м 7 см = 370 см
25 км 40 м = 25040 м +
Комментарий: Проверяется готовность осуществить проверку выполненной работы..
Задача №2.
Четыре ученика, отвечая у доски, получили следующие результаты:
512*26=13312
623*18=12214
34*317=10771
405*25=10125
Выясни, кто из них правильно выполнил умножение?
Решение:
512*26=13312
623*18=11214
34*317=10778
405*25=10125
Ответ: 1 и 3
Комментарий: проверяется готовность контролировать процесс и результат выполнения учебной задачи: "Кто правильно выполнил умножение".
Задача № 3.
Пользуясь оценкой, сравните значение каждого произведения с данным числом:
198*5 и 1000
496*3 и 1500
253*4 и 1000
253*6 и 1500
Решение:
198*5 < 1000
496*3 < 1500
253*4 > 1000
253*6 > 1500
Комментарий: выбирать действия в соответствии с поставленной задачей и условиями ее реализации.
III. Прогнозирование.
Задача №1. Реши задание.
Какая из данных величин выражает длину парты?
120см
120м
120дм
120мм
Комментарий. Проверяется способность предвидеть возможность получения результата.
Решение 120см
Задача №2. Сравните числа, в которых некоторые цифры заменены звездочками.
а)7**** и 69***; б) ***** и ***.
Комментарий. Проверяется способность применения причинно-следственных связей, способность предвидеть результат.
Решение а)7**** > 69***; б) ***** > ***.
Задача №3. Реши задачу.
На одном участке школьники вырастили 360 кг картофеля, на другом в два раза больше. Часть всего картофеля оставили на семена, а остальной израсходовали на горячие завтраки. Сколько кг картофеля израсходовали на горячие завтраки?
Комментарий. Проверяется возможность предвосхищать результат с учётом имеющихся знаний, а также выявлять и прогнозировать причины трудностей.
Решение Недостающее данное: какую часть картофеля оставили на семена?
IV. Коррекция
Задача № 1.
Учитель предложил округлить до миллионов число 26547049.Три ученика дали разные ответы:
2654704926000000
265470492700000
2654704926500000
Объясни, какую ошибку допустил каждый, и дайте правильный ответ.
Решение:
Первый не добавил к классу миллионов 1, у второго не хватает нуля, третий неправильно определил класс миллионов.
Ответ:27000000.
Комментарий: вносить необходимые коррективы в действие после его завершения на основе его оценки и учета сделанных ошибок.
Задача № 2.
Маше и Лене предложили построить самопересекающуюся замкнутую ломанную из 4 звеньев.
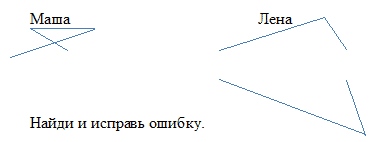
Комментарий: вносить необходимые коррективы в действие после его завершения на основе его оценки и учета сделанных ошибок.

Задача № 3.
Определите, правильно ли указан порядок действий. Если нет, то укажите правильный.
24 + 15* (40-31)
189 - 120:3 - 7 * 7
12*40 - 128:8
16:(112 - 27*4)
Решение:
24+15*(40-31)
89-120: 3 - 7 * 7
12*40 - 128:8
16:(112 - 27*4)
Комментарий: устанавливать соответствие полученного результата поставленной цели.
Познавательные универсальные учебные действия
I. Общеучебные.
Задача № 3.
В одной корзине лежало 24 кг яблок, а в другой лежали груши. Когда в корзину с грушами положили еще 8 кг груш, их стало на 10 кг больше, чем яблок.
Сколько кг груш было в корзине? Реши задачу разными способами.
Решение:
По действиям
24+10=34 (кг) - стало груш
34-8=26 (кг) - было груш
Ответ: 26 кг
Выражением:
(24+10)-8=26(кг)
Ответ: 26 кг груш было в корзине.
Комментарий: проверяется умение ориентироваться в разнообразии способов решения задач.
Задача № 2
На складе было 5ц 40кг овощей. Морковь составляла всех овощей, а картофель - всех овощей. На сколько масса моркови меньше массы картофеля? Какое решение ты считаешь рациональным? Отметь его.
Решение: 5т 40кг=5040кг
5040:9*1=560 (кг)
5040:9*4=2240 (кг)
2240-560=1680 (кг)
5т 40кг=5040кг
(овощей)
(кг)
Ответ: 5т 40кг=5040кг
(овощей)
2) (кг)
Комментарий: проверяется способность выбрать (определить) рациональный способ решения среди других верных решений задачи.
Задача №3.
Пете нужно купить 5кг апельсин и 2 кг банан. Килограмм апельсин стоит 52р, а килограмм бананов в 1,3раза дешевле. Сколько стоит вся покупка?
Решение:
1) 52:1,3=40 (р) стоит килограмм бананов
2) 52*5=260 (р) стоят апельсины
3) 40*2=80 (р) стоят бананы
4) 260+80=340 (р) стоит вся покупка
Ответ: 340 рублей
Комментарий: Проверяется способность алгоритмизировать ход решения.
II. Знаково-символические.
Задача №1. Используя рисунок, составьте уравнение (рисунок 1)
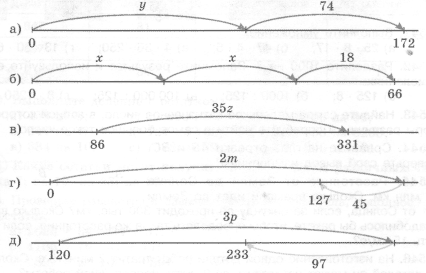
Комментарий. Проверяется готовность использования знаково-символического средства; использования схем для составления уравнений.
Решение а) у + 74 = 172; б) х+х+18 = 66; в) 86+35 z =331; г) 2m - 45 =127; д)120+3p - 97 =233.
Задача №2. (рисунок 2)

Комментарий. Проверяется готовность решения задач на движения, используя знаково-символическое представление (схема к задаче).
Решение
1) 3,75 + 4,5 = 8,25 (км/ч) - скорость сближения
2) 5,7+15,2=20,9(км/ч)- скорость удаления
3) 76,5+ 43,2 = 119,7 (км/ч) - скорость удаления
4)10,2 - 4,6 = 5,6 (км/ч)- скорость удаления
Задача №3. Заполни таблицу, решая задачу.
Всадник проехал 80 км за 5 часов. Сколько времени потратит на этот путь велосипедист, если его скорость на 24 км/ч больше скорости всадника?
| | Скорость (км/ч) | Время (ч) | Расстояние (км) |
| Всадник | | | |
| Велосипедист | | | |
Комментарий. Проверяется готовность выбирать из текста необходимую информацию, представлять ее в таблице, учитывая одновременно несколько условий.
Решение
| | Скорость (км/ч) | Время (ч) | Расстояние (км) |
| Всадник | 16 | 5 | 80 |
| Велосипедист | 40 | 2 | 80 |
III. Логические
Задача №1
Найди, что объединяет эти дроби?
Решение:
Комментарий: проверяется готовность обнаружить общее свойство группы сократимых обыкновенных дробей
| | 23 | 56 |
| 65 | | |
| 14 | | 44 |
| 26 | 23 | 56 |
| 65 | 35 | 5 |
| 14 | 47 | 44 |
Задача №2
Восстанови магический квадрат
Решение:
Комментарий: проверяется умение осуществлять анализ
Объектов с выделением существенных и несущественных признаков
Задача №3
а) Вычислить сумму натуральных чисел от 1 до 100.
Решение.
Для вычисления суммы 1+2+3+4+: +97+98+99+100 сгруппируем слагаемые таким образом: (1+100)+(2+99)+(3+98)+:+(50+51).
Каждое слагаемое равно _______. Всего _______ слагаемых.
Сумма равна __________. ___________ = ___________
б) Вычисли сумму натуральных чисел от 1 до 60.
Решение.____________________________________________________________.
Ответ: А) Каждое слагаемое равно 101. Всего 50 слагаемых.
Сумма равна 101 * 50 = 5050
Б) 61 *30 = 1830.
Комментарий: Проверяется умение устанавливать причинно-следственные связи, строить лКоммуникативные универсальные учебные действия.
Инициативное сотрудничество.
Задача №1. Как найти периметр прямоугольника, квадрата? Предложите разные способы. Какие из этих способов лучше?
Комментарий. Проверяется способность формулировать собственное мнение, предлагать помощь и сотрудничество.
Решение
1. Для нахождения периметра прямоугольника и квадрата надо сложить сумму длин всех сторон.
2.Для нахождения периметра прямоугольника надо вычислить удвоенную сумму длины и ширины. Для нахождения периметра квадрата надо его сторону умножить на 4.
Второй способ лучше, так как более эффективный.
Задача №2. Реши задачу.
По дороге движутся навстречу друг другу пешеход и велосипедист. Сейчас расстояние между ними 52 км. Скорость пешехода 4 км/ч, а скорость велосипедиста 9 км/ч. Поставьте вопросы к задаче и решите ее.
Комментарий. Проверяется способность задавать вопросы, необходимые для организации собственной деятельности и сотрудничества.
Решение. Какое расстояние будет между ними через 1час; через 2 часа
4+9=13 (км/ч)- скорость сближения
52 - 13 =39( км) -через 1 час
39 - 13 = 26(км) - через 2 часа.
Встретятся ли пешеход и велосипедист через 3 часа?
3*(4+9)=39 км преодолеют вместе за 3 часа. Так как расстояние между ними сейчас 52, что не равно этому пройденному пути, ответ: не встретятся.
Через сколько часов пешеход и велосипедист встретятся?
4+9 = 13 (км/ч) - скорость сближения
52:13 = 4 (ч)
Ответ: через 4 часа.
Задача №3.Реши задачу.
Каков рост каждого ученика? Кто ниже (выше) Тани? (рисунок 3)

Комментарий. Проверяется способность проявлять активность во взаимодействии для решения коммуникативных и познавательных задач, формулировать свое решение.
Решение. Рост Сережи 160см, Люды -120см, Тани-150см, Вани-140см, Петра-100см. Значит, ниже Тани: Люда, Петр, и Ваня. Выше Тани - Сережа.
