Задание1 информатика. Задание 1 Квашенко. Выполним задание для данных, представленных в следующей таблице
 Скачать 479.22 Kb. Скачать 479.22 Kb.
|
|
Выполним задание для данных, представленных в следующей таблице:
Для нахождения значения y будем использовать x= 21. Оформим таблицу с данными на рабочем листе электронной таблицы так, как показано на рисунке 1. Построим по данным таблицы диаграмму точечного типа. Для этого выделим данные и выполним команды «Вставка – Диаграммы – Точечная». Наведем курсор мыши на любую точку построенного графика и нажмем правую кнопку. В появившемся контекстном меню следует выбрать команду «Добавить линию тренда…». Откроется диалоговое окно «Формат линии тренда» (рис. 2), в котором выберем тип линии тренда «Линейная» и установим флажки «Показывать уравнение на диаграмме» и «Поместить на диаграмму величину достоверности аппроксимации (R^2)». 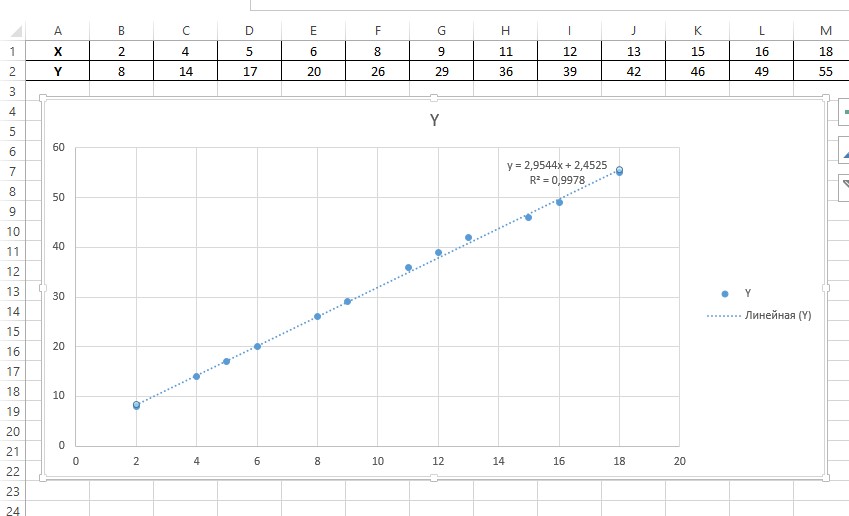 Рис. 1. Точечная диаграмма, соответствующая таблице значений функции 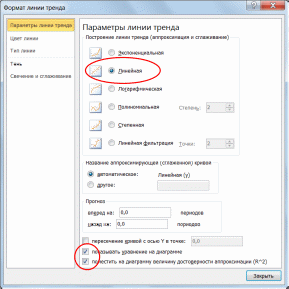 Рис. 2. Выбор типа линии тренда К диаграмме будет добавлена линия тренда, построенная по методу наименьших квадратов для случая линейной аппроксимации. Кроме того, будет выведен вид линейной аппроксимирующей функции y = 2,9544х+2,4525и коэффициент достоверности аппроксимации R^2 = 0,9978 (рис. 3). Аналогично построим линии тренда с использованием полинома второго порядка и степенной функции. Величина достоверности аппроксимации характеризует степень близости аппроксимирующей функции к данным таблицы, по которой было выполнена аппроксимация. Чем ближе R^2 к 1, тем более достоверной является аппроксимация. Сравнение значений величин достоверности аппроксимации для разных аппроксимирующих функций в нашем случае показывает, что наибольшее значение R^2 = 0,9987 соответствует аппроксимации с помощью полинома второго порядка. 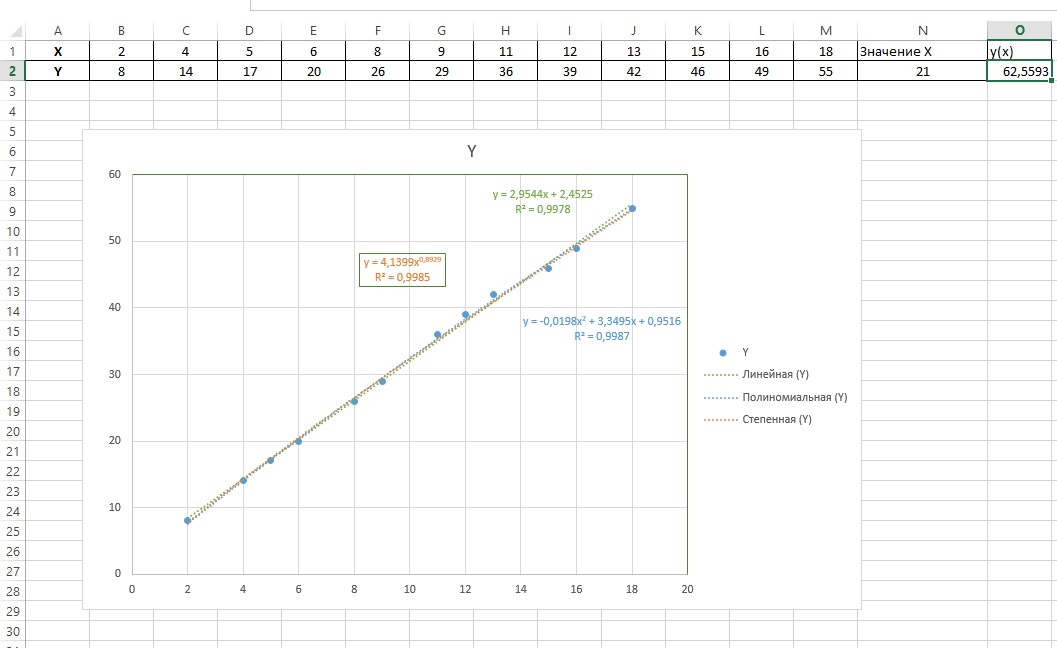 Рис. 3. Линии тренда на диаграмме Используем полученную полиномиальную функцию для вычисления значения y для x= 21. Для этого в ячейку N2 введем значение 21, а в ячейку O2 – формулу для расчета y: = – 0,0198 · N2^2 + 3,3495· N2 +0,9516 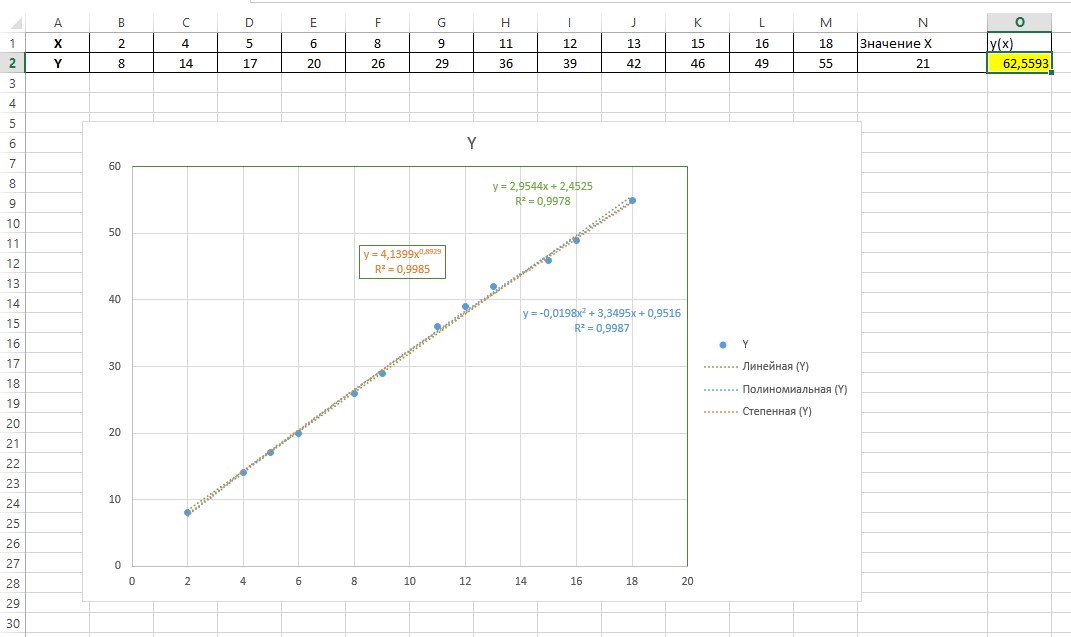 Рис. 4. Результат выполнения задания Расчет показывает, что для x= 21 приближенное значение y, полученное с помощью аппроксимирующей функции, равно 62,5593. |
