измерение Лабораторные. Выполняемые лабораторные работы на учебном лабораторном стенде нтц05. 08. 1 Электрические измерения с мпсо

Название	Выполняемые лабораторные работы на учебном лабораторном стенде нтц05. 08. 1 Электрические измерения с мпсо
Дата	13.03.2023
Размер	6 Mb.
Формат файла
Имя файла	измерение Лабораторные.docx
Тип	Документы #984268
страница	15 из 34

1 ... 11 12 13 14 15 16 17 18 ... 34

Часть 5.4. Измерение индуктивности мостом Максвелла.

Порядок выполнения

Собрать схемы, представленные на рисунке5.3ирисунке5.7.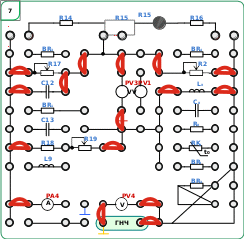

Рисунок 5.7

Включить компьютер и запустить программу «DiSco».
Настройте первый канал осциллографа и запустите его в режиме много кратного запуска.
Перед включением стенда убедится, что все остальные переключатели находятся в начальном положении (выключены).
Включить стенд автоматическим выключателем QF1.
По осциллограмме в программе «DiSco» задайте выходной сигнал генератора (с помощью органов управления генератором R20, R21и SA19) со следующими параметрами: Форма:Синус;Амплитуда10В;Смещение0В;Частота 1кГц.
Установите резистор R19 в максимальное значение 100 Ом.
Установите резистор R17 в максимальное положение 1 кОм.
Изменяя значение сопротивлений R2 и R19 добиться показания прибором PV3близкого кнулюзначения.

Значение сопротивления R2 изменяется галетными переключателями 1x1000, 1x100, 1x10, 1x1 в следующем виде: R2=1000∙n_1x1000+100∙n_1x100+10∙n_1x10+n_1x1 Ом соответственно для каждого переключателя, где n – положение каждого переключателя соответственно.

Не меняя номиналов резисторов, остановить программу «DiSco»,записать значение резисторов R2,R17,R19.
Выключить стенд в следующем порядке:
- Выключить стенд автоматическим выключателем QF1;
- Вернуть переключатели резисторов R2,R17,R19в начальное состояние «0»;
- Убрать все перемычки.



Рассчитать неизвестную индуктивность L_Xпо формуле:

𝐿_𝑋 = 𝑅₂(𝑅₁₉ + 𝑅₁₈)𝐶₁₂

Вычислить по результатам измерения абсолютную погрешность измерения индуктивности. Принять фактическую индуктивность L_X_ФАКТ=0,082Гн,емкость С₁₂=0,1 мкФ.

^∆𝐿⁼^𝐿𝑋 И3M ⁻^𝐿𝑋 ΦAKT

Вычислить относительную погрешность.

𝛾₀

₌∆𝐿

^𝐿𝑋ΦAKT

· 100%

Примечание:

В данной работе наибольшая точность достигается если проводить опыт с частотой 5кГц. Для этого равновесие моста устанавливается не по прибору PV3, а по показаниям осциллографа.

Лабораторная работа №6. Измерение параметров элементов электрических схем резонансным методом

Цельработы:

Измерение емкости резонансным методом.
Измерение емкости резонансным методом с замещением при последовательном включении измеряемой емкости.
Измерение емкости резонансным методом с замещением при параллельном включении измеряемой катушки.
Измерение индуктивности резонансным методом.
Измерение индуктивности резонансным методом с замещением при последовательном включении измеряемой катушки.
Измерение индуктивности резонансным методом с замещением при параллельном включении измеряемой катушки.

Краткие теоретические сведения.

Принцип резонансного метода измерения заключается в определении собственной частоты колебательного контура, составленного из образцового и измеряемого элементов. Значение измеряемого параметра вычисляется из формулы:

f = ¹

²√^LC

Резонансный метод применяется на высоких частотах для измерения индуктивности,

емкости и сопротивления потерь в них. Главное преимущество этого метода состоит в том, что измерения можно выполнять на рабочих частотах.

Измерительная установка состоит из высокочастотного генератора, измерительного контура и индикатора резонанса. Погрешность резонансного метода измерения определяется неточностью настройки колебательного контура в резонанс с частотой генератора, погрешностью установки частоты и ее нестабильностью за время измерения, а также относительной величиной паразитных параметров измерительного устройства.

Для уменьшения погрешности измерения применяют следующие меры. Настраиваемый элемент измерительного контура (обычно образцовый конденсатор переменной емкости) снабжают верньерным устройством с соответствующим замедлением или параллельно основному образцовому конденсатору присоединяют второй (вспо- могательный) малой емкости, так называемый электрический нониус. Эти меры позволяют плавно устанавливать и фиксировать момент резонанса. Выбирают генератор с возможно лучшей стабильностью частоты и точностью ее установки. Для уменьшения вносимого в контур сопротивления генератора последний слабо связывают с измерительным контуром. Связь осуществляют емкостную или индуктивную. В качестве индикатора используют ламповый вольтметр с большим входным сопротивлением и известной малой емкостью. Монтаж измеряемого контура обычно выполняют без проводов, его элементы непосредственно соединяют друг с другом. Величина потерь в образцовых конденсаторах пренебрежимо мала, а в образцовых катушках известна и может быть учтена.

Большое влияние на погрешность измерения оказывает собственнаяемкостькатушкииндуктивностиCL. Это не поддающаяся точному расчету распределенная вдоль обмотки катушки емкость, которую условились считать сосредоточенной при рабочих частотах f, много меньших собственной частоты катушки

f = ¹

^L ²√^LC

Наличие собственной емкости в катушке индуктивности приводит к получению в

результате измерения некоторых действующих значений индуктивности L_Ди сопротивления

потерь R_Д, отличающихся от истинных значений Lи R_L. Связи между Lи L_Д, R_Lи R_Длегко установить, приравняв проводимости эквивалентных схем друг другу:

Д
_L₌_LC + C_L

C

C+C_L ²

R_Д = R_L ( _C)

Очевидно, что желательно стремиться к соблюдению условия C>>C_L, где С— емкость

измерительного контура. Можно выразить соотношение между Lи L_Д, а также R_Lи R_Дчерез частоту:

L = ^L

^Д f ²

1 − (_f_L)

и

_R₌ R_L

^Д f ² 2

(1 − (_f_L) )

Отсюда очевидно, что рабочая частота генератора f должна быть во много раз ниже собственной частоты катушки f_L.

Измерениеиндуктивностирезонансным методом удобно выполнять тремя способами, в зависимости от ожидаемого ее значения. Первый способ (рисунок 6.1.а) применяют для измерения значений индуктивности порядка сотен микрогенри. Измерительный колебательный контур настраивают в резонанс по максимальному показанию индикатора. Настройку осуществляют изменением частоты fгенератора или емкости С_ОБобразцового конденсатора. Считывают эти значения по соответствующим шкалам и вычисляют истинную индуктивность:

L = ¹

^X 4 ²f²(C + C_L)

где С— емкость измерительного контура, C = C_OБ + C_BX — входная емкость индикатора.

Если собственная емкость катушки C_Lнеизвестна, то вычисляют действующее значение индуктивности

^LXД

₌1

4 ²f²C

Второй способ (рисунок 6.1.б) применяют для измерения значений индуктивности порядка десятков микрогенри. Здесь резонансный метод сочетается с замещением измеряемой индуктивности образцовой емкостью. Измерительный контур составляют из образцового переменного конденсатора и вспомогательной катушки L_B. Измерение выполняют дважды, настраивая контур в резонанс при неизменной выбранной частоте генератора: один раз без измеряемой катушки, второй — включив ее последовательно со вспомогательной.

Рисунок6.1.Три варианта измерения индуктивности:

а— резонансным методом;

б — резонансным с замещением при последовательном включении измеряемой катушки;

в— то же при параллельном включении

Заметив значения емкостей образцового конденсатора при настройках в резонанс C_ОБ1

и C_ОБ2можно написать:

откуда:

f = ¹

²√^LBCOБ1

₌1

2 √⁽L_B + L_X⁾C_OБ2

^LXД

= L_B

^COБ1^{− C}OБ2 ^COБ2

Если вспомогательная катушка является образцовой, то задача решена; если же она

1
случайна и величина индуктивности ее неизвестна, последнюю следует исключить из формулы,

подставив ее значение из первого равенства L_B = ₄₂_f₂_C_OБ1. В результате получаем:

^LXД

₌^COБ1 ^{− C}OБ2 ⁴²^f²^COБ1^COБ2

Измеряемая и вспомогательная катушки не должны иметь связи друг с другом за счет

общего магнитного поля.

Третий способ (рисунок 6.1.в) используют для измерения больших значений индуктивностей — до сотен миллигенри. Измерение выполняется способом, аналогичным предыдущему, с той разницей, что измеряемая катушка индуктивности включается параллельно вспомогательной. Величина действующей индуктивности

L = L

C_OБ1₌1

^{XД B}^COБ2 ⁻^COБ1

4 ²f²(C_OБ2− C_OБ1)

Измерениеемкостирезонансным методом выполняют тремя способами. Первый способ чисто резонансный (рисунок 6.2.а). Контур составляют из образцовой катушки с известными параметрами и C_Lи измеряемого конденсатора. Контур настраивают в резонанс изменением частоты генератора и неизвестную емкость вычисляют по формуле:

C = ¹

^X 4 ²f²L_OБ

− C_L

− C_BX

Погрешность измерения определяется погрешностью всех входящих в это выражение величин, и для ее уменьшения применяют способы, сочетающие метод резонанса с замещением. Измерительный контур составляют из образцового конденсатора переменной емкости и вспомогательной катушки.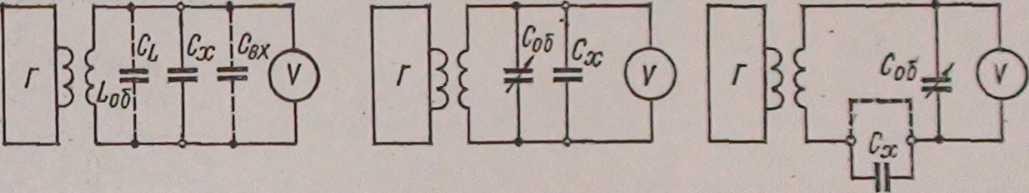

Рисунок6.2.Три варианта измерения емкости:

а— резонансным методом;

б— резонансным с замещением при параллельном включении измеряе- мого конденсатора;

в— то же при последовательном включении.
Если измеряемая емкость не выходит за пределы изменения емкости образцового конденсатора (от C_MINдо C_MAX), то используют схему, приведенную на рисунке 6.2.б. Первую настройку выполняют без измеряемого конденсатора изменением частоты генератора при установленном значении емкости образцового конденсатора С_ОБ1вблизи ее максимальной величины. Затем включают параллельно образцовому конденсатору измеряемый C_Xи, не меняя частоты генератора, вторично настраивают контур в резонанс.

Очевидно, что емкость С_ОБ2при резонансе будет меньше С_ОБ1на величину C_X, т. е.

^CX ⁼^COБ1 ⁻^COБ2

Если емкость измеряемого конденсатора больше максимальной емкости образцового, то их вначале соединяют последовательно (рисунок 6.2.в) и контур настраивают в резонанс изменением частоты генератора при значении С_ОБ1вблизи ее максимальной величины. Затем измеряемый конденсатор отключают и, настраивая контур образцовым конденсатором переменной емкости при неизменной частоте генератора, восстанавливают резонанс. Полученное при этом второе значение образцовой емкости C_ОБ2позволяет вычислить измеряемую емкость

_{C =}^COБ1^COБ2 ^X^COБ1^−COБ2

1 ... 11 12 13 14 15 16 17 18 ... 34