измерение Лабораторные. Выполняемые лабораторные работы на учебном лабораторном стенде нтц05. 08. 1 Электрические измерения с мпсо
 Скачать 6 Mb.
|
Краткие теоретические сведения.Метод вольтметра и амперметра - косвенный способ определения различных сопротивлений, позволяющий ставить элемент с определенным сопротивлением в рабочие условия. Этот метод основан на использовании закона Ома для участка цепи, сопротивление RXкоторого определяется по известному падению напряжения UXна нем и току IXтак: 𝑅𝑋 = 𝑈𝑋 𝐼𝑋 Существуют различные способы измерения падения напряжения UXи тока IX(Рисунок 4.1.) 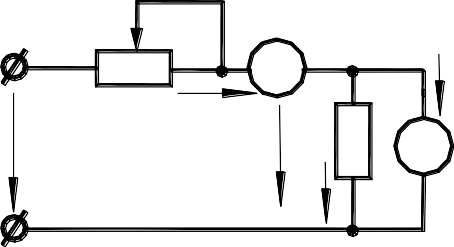 + АRр I U Uх Rх Iв +  V Iх Rв - - а) б)Рисунок4.1. Измерительные части приведенных схем не обеспечивают одновременное измерение напряжения UXи тока IX. Так 1-я схема (Рисунок 4.1.б.) позволяет измерить с помощью вольтметра напряжение UX, а амперметр дает возможность определить ток I, равный сумме IXи IВ, из которых последний является током обмотки вольтметра. В этом случае определяемое сопротивление: 𝑅 = 𝑈𝑋 =𝑈𝑋 = 𝑈𝑋 𝑋 𝐼𝑋 𝐼 − 𝐼𝐵 𝐼 − 𝑈𝑋 𝑅 𝐵 где RВ- сопротивление вольтметра. Во второй схеме амперметр учитывает ток IX, но вольтметр показывает напряжение U, равное сумме падений напряжений UXна сопротивлении RXи UAна амперметре. Поэтому определяемое сопротивление:   𝑅 = 𝑈𝑋 = 𝑈−𝑈𝐴 = 𝑈 − 𝑈𝐴 = 𝑈 − 𝑅 𝑋 𝐼𝑋 𝐼𝑋 𝐼𝑋 𝐼𝑋 𝐼𝑋 𝐴 где RA- сопротивление амперметра. Следовательно, если при расчете определяемого сопротивления учитывать сопротивления приборов, то все схемы равноценны. Если определяемое сопротивление RXмало по сравнению с сопротивлением вольтметра RB, током IBможно пренебречь и, применяя первую схему (Рисунок 4.1.а.), находить сопротивление RX так: 𝑅𝑋 = 𝑅′𝑋 = 𝑈𝑋 𝐼 допуская относительную погрешность: 𝛾 = 𝑅′𝑋−𝑅𝑋 = − 𝑅′𝑋 = − 𝑅𝑋 0 𝑅𝑋 𝑅𝐵 𝑅𝑋 + 𝑅𝐵 В этих случаях, когда определяемое сопротивление RXсравнимо с сопротивлением вольтметра RBи пренебречь током IBнельзя, следует пользоваться второй схемой (Рисунок 4.1.б.) и при расчете не учитывать падение напряжения UAна амперметре, определяя сопротивление RXтак: 𝑅𝑋 = 𝑅′𝑋 = 𝑈 𝐼𝑋при относительной погрешности измерения: 𝛾 = 𝑅′𝑋−𝑅𝑋 = 𝑅𝐴= 𝑅𝐴 0 𝑅𝑋 𝑅𝑋 − 𝑅𝐴 𝑅𝑋 Для выявления пределов целесообразности использования той или другой схемы следует приравнять относительные погрешности и, а затем найти значение сопротивления RX, для которого обе схемы равноценны: 𝑅𝑋= 𝑅𝐴 или 𝑅𝑋 + 𝑅𝐵 𝑅𝑋 𝑋 Откуда 𝑅2 − 𝑅𝐴𝑅𝑋 − 𝑅𝐵𝑅𝐴 = 0  𝑅𝑋 ≅ √𝑅𝐵𝑅𝐴 Следовательно, для сопротивлений 𝑅𝑋 √𝑅𝐵𝑅𝐴 предпочтительна схема рисунок 4.1.а., а для сопротивлений 𝑅𝑋 √𝑅𝐵𝑅𝐴 - схема рисунок 4.1.б. Первую из них называют схемой определения "малых" сопротивлений, а другая – схемой для определения "больших"сопротивлений. При определении сопротивлений методом вольтметра и амперметра следует выбирать магнитоэлектрические приборы с такими пределами измерений, чтобы показания их были близки к номинальным значениям, т.к. это обеспечивает меньшие погрешности измерения. Часть4.1Измерение сопротивления косвенным методом (амперметром и вольтметром). Порядок выполнения Собрать схему, представленную на рисунке4.2.В качестве неизвестного сопротивления большой величины будет использован резистор R3. Перед включением стенда убедится, что все остальные переключатели находятся в начальном положении (выключены). Включить стенд автоматическим выключателем QF1. Убедиться, что регуляторы напряжения ЛАТРанаходятся в начальных положениях «0»(в крайнем левом положении). Установить тумблер SA10вниз, SA12вверх. Подключить питание ЛАТРаTV1к исследуемой цепи тумблером SA1. Постепенно увеличивать напряжение ЛАТРомдо 30-40В(контролировать по прибору PV3). A A R1 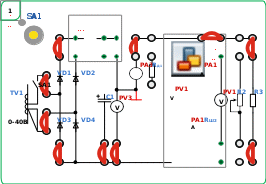 |