Выражения и их преобразования 7 кл
 Скачать 71.32 Kb. Скачать 71.32 Kb.
|
|
Согласовано: заместитель директора по УВР МКОУ «Покровская СОШ» Косогор Евгения Николаевна «___»_____________________ Утверждаю: директор МКОУ «Покровская СОШ» Иванова Светлана Анатольевна Приказ №________от________ Контрольные работы Математика 7 класс 2014 АЛГЕБРА Контрольная работа по теме: «Выражения и их преобразования» 7 кл. Вариант 1 1°. Найдите значение выражения: 6x – 8y при x = 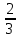 , y = , y =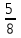 . .2°. Сравните значения выражений – 0,8х – 1 и 0,8х – 1 при х = 6. 3°. Упростите выражение: а) 2х – 3у – 11х + 8у, б) 5 (2а + 1) – 3, в) 14х – (х – 1) + (2х + 6). 4. Упростите выражение и найдите его значение: – 4 (2,5а – 1,5) + 5,5а – 8 при а = – 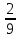 . .5. Из двух городов, расстояние между которыми s км, одновременно навстречу друг другу выехали легковой автомобиль и грузовик и встретились через t ч. Скорость легкового автомобиля v км/ч. Найдите скорость грузовика. Ответьте на вопрос задачи, если s = 200, t = 2, v = 60. 6. Раскройте скобки: 3х – (5х – (3х – 1)). Контрольная работа по теме: «Выражения и их преобразования» 7 кл. Вариант 2 1°. Найдите значение выражения: 16а + 2y при а = 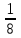 , y = – , y = –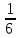 . .2°. Сравните значения выражений 2+ 0,3а и 2 – 0,3а при а = – 9. 3°. Упростите выражение: а) 5а + 7b – 2а – 8b, б) 3 (4x + 2) – 5, в) 20b – (b – 3) + (3b – 10). 4. Упростите выражение и найдите его значение: – 6 (0,5x – 1,5) – 4,5x – 8 при x= 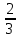 . .5. Из двух городов одновременно навстречу друг другу выехали автомобиль и мотоцикл и встретились через t ч. Найдите расстояние между городами, если скорость автомобиля v1 км/ч, а скорость мотоцикла v2 км/ч. Ответьте на вопрос задачи, если t = 3, v1 = 80, v2= 60. 6. Раскройте скобки: 2p – (3p – (2p – c)). Критерии оценки: «5» - верно выполнены все задания; Контрольная работа №2 по теме: «Уравнения с одной переменной» 7 класс Вариант 1 1°. Решите уравнение: а) 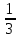 х = 12; б) 6х – 10,2 = 0; х = 12; б) 6х – 10,2 = 0;в) 5x – 4,5 = 3x + 2,5; г) 2х – (6х – 5) = 45. 2°. Таня в школу сначала едет на автобусе, а потом идет пешком. Вся дорога у нее занимает 26 мин. Идет она на 6 мин дольше, чем едет на автобусе. Сколько минут она едет на автобусе? 3. В двух сараях сложено сено, причем в первом сарае сена в 3 раза больше, чем во втором. После того как из первого сарая увезли 20 т сена, а во второй привезли 10т, в обоих сараях сена стало поровну. Сколько всего тонн сена было в двух сараях первоначально? 4. Решите уравнение: 7х – (х + 3) = 3 (2х – 1). Контрольная работа №2 по теме: «Уравнения с одной переменной» 7 класс Вариант 2 1°.Решите уравнение: а) 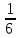 х = 18; б) 7х + 11,9=0; х = 18; б) 7х + 11,9=0;в) 6х – 0,8 = 3х + 2,2; г) 5х – (7х + 7) = 9. 2°. Часть пути в 600 км турист пролетел на самолете, а часть проехал на автобусе. На самолете он проделал путь, в 9 раз больший, чем на автобусе. Сколько километров проехал турист на автобусе? 3. На одном участке было в 5 раз больше саженцев смородины, чем на другом. После того как с первого участка увезли 50 саженцев, а на втором посадили еще 90, на обоих участках саженцев стало поровну. Сколько всего саженцев смородины было на двух участках первоначально? 4. Решите уравнение: 6x – (2х – 5) = 2 (2х + 4). Контрольная работа по теме: «Функции» Вариант 1 1°. Функция задана формулой у = 6х + 19. Определите: а) значение у, если х = 0,5; б) значение х, при котором у = 1; в) проходит ли график функции через точку А (– 2; 7). 2°. а) Постройте график функции у = 2х – 4. б) Укажите с помощью графика, чему равно значение у при х = 1,5. 3°. В одной и той же системе координат постройте графики функций: а) у = – 2х; б) у = 3. 4. Найдите координаты точки пересечения графиков функций у = 47х – 37 и у = – 13х + 23. 5. Задайте формулой линейную функцию, график которой параллелен прямой у = 3х – 7 и проходит через начало координат. Вариант 2 1°. Функция задана формулой у = 4х – 30. Определите: а) значение у, если х = – 2,5; б) значение х, при котором у = – 6; в) проходит ли график функции через точку B(7; – 3). 2°. а) Постройте график функции у = – 3х + 3. б) Укажите с помощью графика, при каком значении х значение у = 6; у = 3. 3°. В одной и той же системе координат постройте графики функций: а) у = 0,5x; б) у = – 4. 4. Найдите координаты точки пересечения графиков функций у = – 38x + 15 и у = – 21х – 36. 5. Задайте формулой линейную функцию, график которой параллелен прямой у = – 5х + 8 и проходит через начало координат. Критерии оценки: «5» - верно выполнены все задания; «4» - верно выполнены 4 задания; «3» - верно выполнены 3 задания. Контрольная работа по теме: «Степень с натуральным показателем» Вариант 1 1°. Найдите значение выражения 1 – 5х2 при х = – 4. 2°. Выполните действия: а) у7 ∙ у12; б) у20 : у5; в) (у2)8; г) (2у)4. 3°. Упростите выражение: а) – 2аb3 · 3а2 · b4; б) (–2а5b2) 3. 4°. Постройте график функции у = х2. С помощью графика определите значение у при х = 1,5; х = -1,5. 5. Вычислите: 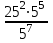 . .6. Упростите выражение: а) 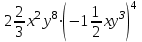 ; б) хn - 2 ∙ х3 - n ∙ х. ; б) хn - 2 ∙ х3 - n ∙ х.Вариант 2 1°. Найдите значение выражения – 9p3 при p = – 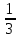 . .2°. Выполните действия: а) c3 ∙ c22; б) c18 : c6; в) (c4)6; г) (3c)5. 3°. Упростите выражение: а) – 4x5y2 ∙ 3xy4 ; б) (3x2y3) 2. 4°. Постройте график функции у = х2. С помощью графика определите, при каких значениях х значение у равно4. 5. Вычислите: 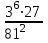 . .6. Упростите выражение: а) 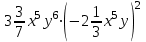 ; б) (аn + 1)2 : а2n. ; б) (аn + 1)2 : а2n.Критерии оценки: «5» - верно выполнены все задания; «4» - верно выполнены 5 заданий; «3» - верно выполнены 4 задания. Контрольная работа по теме: «Сумма и разность многочленов. Произведение многочлена и одночлена» Вариант 1 1°. Выполните действия: а) (3а – 4ах + 2) – (11а – 14ах), б) 3у2 (у3 + 1). 2°. Вынесите общий множитель за скобки: а) 10аb– 15b2, б) 18а3+ 6а2. 3°. Решите уравнение: 9х – 6(х – 1) = 5(х + 2). 4°. Пассажирский поезд за 4 ч прошел такое же расстояние, какое товарный за 6 ч. Найдите скорость пассажирского поезда, если известно, что скорость товарного на 20 км/ч меньше. 5. Решите уравнение: 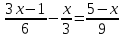 . .6. Упростите выражение: 2а (а + b – с) – 2b (а – b– с) + 2с (а – b+ с). Вариант 2 1°. Выполните действия: а) (2а2 – 3а + 1) – (7а2 – 5а), б) 3x (4x2 – x). 2°. Вынесите общий множитель за скобки: а) 2xy– 3xy2, б) 8b4+ 2b3. 3°. Решите уравнение: 7 – 4(3х – 1) = 5(1 – 2x). 4°. В трех шестых классах 91 ученик. В 6 "А" на 2 ученика меньше, чем в 6 "Б", а в 6 "В" на 3 ученика больше, чем в 6 "Б". Сколько учащихся в каждом классе? 5. Решите уравнение: 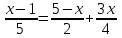 6. Упростите выражение: 3x (x + y + с) – 3y (x – y– с) – 3с (x + y– с). Критерии оценки: «5» - верно выполнены все задания; «4» - верно выполнены 5 заданий; «3» - верно выполнены 4 задания. Контрольная работа по теме: «Произведение многочленов» Вариант 1 1°. Выполните умножение: а) (с + 2) (с – 3); б) (2а – l) (3а + 4); в) (5х – 2у) (4х – у); г) (а – 2) (а2 - 3а + 6). 2°. Разложите на множители: а) а(а + 3) – 2(а + 3), б) аx – аy + 5x – 5y. 3. Упростите выражение – 0,lx (2x2 + 6) (5 – 4x2). 4. Представьте многочлен в виде произведения: а) х2 – ху – 4х + 4у, б) аb – ас – bx+ сх + с – b. 5. Из прямоугольного листа фанеры вырезали квадратную пластинку, для чего с одной стороны листа фанеры отрезали полосу шириной 2 см, а с другой, соседней, – 3 см. Найдите сторону получившегося квадрата, если известно, что его площадь на 51 см2 меньше площади прямоугольника. Вариант 2 1°. Выполните умножение: а) (а – 5) (а – 3); б) (5x + 4) (2x – 1); в) (3p + 2c) (2p + 4c); г) (b– 2) (b2 + 2b- 3). 2°. Разложите на множители: а) x (x – y) + а (x– y), б) 2а – 2b + cа – cb. 3. Упростите выражение 0,5х (4x2 – 1) (5x2 + 2). 4. Представьте многочлен в виде произведения: а) 2а – аc – 2c + c2, б) bx + by – x– y – аx –аy. 5. Бассейн имеет прямоугольную форму. Одна из его сторон на 6 м больше другой. Он окружен дорожкой, ширина которой 0,5 м. Найдите стороны бассейна, если площадь окружающей его дорожки 15 м2. Критерии оценки: «5» - верно выполнены все задания; «4» - верно выполнены 3, 4 заданий; «3» - верно выполнены 2 задания. Контрольная работа по теме: «Формулы сокращенного умножения» Вариант 1 1°. Преобразуйте в многочлен: а) (у–4)2; б) (7х + а)2; в) (5с – 1) (5с + 1); г) (3а + 2b) (3а – 2b). 2°. Упростите выражение (а – 9)2 – (81 + 2а). 3°. Разложите на множители: а) х2 – 49; б) 25x2 – 10ху + у2. 4. Решите уравнение: (2 – х)2 – х (х + 1,5) = 4. 5. Выполните действия: а) (y2 – 2а) (2а + y2); б) (3х2 + х)2; в) (2 + m)2 (2 – m)2. 6. Разложите на множители: а) 4x2y2 – 9а4; б) 25а 2 – (а + 3)2; в) 27m 3 + n3. Вариант 2 1°. Преобразуйте в многочлен: а) (3а + 4)2; б) (2х –b)2; в) (b + 3) (b – 3); г) (5y – 2x) (5y + 2x). 2°. Упростите выражение: (c + b) (c – b) – (5c2 – b2). 3°. Разложите на множители: а) 25y2 – а2; б) c2 + 4bc + 4b2. 4. Решите уравнение: 12 – (4 – х)2 = х (3 – x). 5. Выполните действия: а) (3x + y2) (3x – y2); б) (а3 – 6а)2; в) (а – x)2 (x + а)2. 6. Разложите на множители: а) 100а4 – 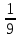 b2; б) 9x2 – (x – 1)2; b2; б) 9x2 – (x – 1)2;в) x3 + y6. Критерии оценки: «5» - верно выполнены все задания; «4» - верно выполнены 4, 5 заданий; «3» - верно выполнены 3 задания. Контрольная работа по теме: «Преобразование целых выражений» Вариант 1 1°. Упростите выражение: а) (х – 3) (х – 7) – 2х (3х – 5); б) 4 а (а – 2) – (а – 4)2; в) 2 (m+ 1)2 – 4m. 2°. Разложите на множители: а) х3 – 9х; б) – 5а 2 – 10аb – 5b2. 3. Упростите выражение (у2 – 2у)2 – у2(у + 3)(у – 3) + 2у(2у2 + 5). 4. Разложите на множители: а) 16x4 – 81; б) x2 – x – y2 –y. 5. Докажите, что выражение х2 – 4х + 9 при любых значениях х принимает положительные значения. Вариант 2 1°. Упростите выражение: а) 2х (х – 3) – 3х (х + 5); б) (а + 7) (а – 1) + (а – 3)2; в) 3 (y + 5)2 – 3y2. 2°. Разложите на множители: а) c2 – 16c, б) 3а 2 – 6аb + 3b2. 3. Упростите выражение (3а – а2)2 – а2 (а – 2) (а + 2) + 2а (7 + 3а2). 4. Разложите на множители: а) 81а 4 – 1, б) y2 – x2 – 6x – 9. 5. Докажите, что выражение – а2 + 4а – 9 может принимать лишь отрицательные значения. Критерии оценки: «5» - верно выполнены все задания; «4» - верно выполнены 3, 4 заданий; «3» - верно выполнены 2 задания. Контрольная работа по теме: «Системы линейных уравнений» Вариант 1 1  °. Решите систему уравнений: 4х + у = 3, °. Решите систему уравнений: 4х + у = 3,6х – 2у = 1. 2°. Банк продал предпринимателю г-ну Разину 8 облигаций по 2 000 р. и 3 000 р. Сколько облигаций каждого номинала купил г-н Разин, если за все облигации было заплачено 19 000 р.? 3  . Решите систему уравнений: . Решите систему уравнений:2(3х + 2у) + 9 = 4х + 21, 2х + 10 = 3 – (6х + 5у). 4. Прямая у = kx + b проходит через точки A(3; 8) и В(– 4; 1). Напишите уравнение этой прямой. 5. Выясните, имеет ли решение система  3х - 2у = 7, 3х - 2у = 7,6х - 4у = 1. Вариант 2 1  °. Решите систему уравнений 3х – у = 7, °. Решите систему уравнений 3х – у = 7,2х + 3у = 1. 2°. Велосипедист ехал 2 ч по лесной дороге и 1 ч по шоссе, всего он проехал 40 км. Скорость его на шоссе была на 4 км/ч больше, чем скорость на лесной дороге. С какой скоростью велосипедист ехал по шоссе, и с какой по лесной дороге? 3. Решите систему уравнений  2(3х – у) – 5 = 2х – 3у, 2(3х – у) – 5 = 2х – 3у,5 – (х – 2у) = 4у + 16. 4. Прямая у = kx + b проходит через точки A(5; 0) и В(– 2; 21). Напишите уравнение этой прямой. 5  . Выясните, имеет ли решения система и сколько: . Выясните, имеет ли решения система и сколько:5х – у = 11, –10х + 2у = –22. Критерии оценки: «5» - верно выполнены все задания; «4» - верно выполнены 3, 4 заданий; «3» - верно выполнены 2 задания. Итоговая контрольная работа по алгебре Вариант 1 1°. Упростите выражение: а) 3а2 b ∙ (-5a3b ); б) (2х2у)3. 2°. Решите уравнение 3х – 5 (2х + 1) = 3 (3 – 2х). 3°. Разложите на множители: а) 2ху – 6у2; б) а3 – 4а. 4°. Периметр треугольника АВС равен 50 см. Сторона АВ на 2 см больше стороны ВС, а сторона АС в 2 раза больше стороны ВС. Найдите стороны треугольника. 5. Докажите, что верно равенство (а + с) (а - с) – b (2a - b) – (a – b + c) (a – b - c) = 0. 6. На графике функции у = 5х – 8 найдите точку, абсцисса которой противоположна ее ординате. Вариант 2 1°. Упростите выражение: а) -2ху2 ∙ 3х3у5; б) (-4аb3)2. 2°. Решите уравнение 4 (1 - 5х) = 9 - 3 (6х - 5). 3°. Разложите на множители: а) а2b– аb2; б) 9х – х3. 4°. Турист прошел 50 км за 3 дня. Во второй день он прошел на 10 км меньше, чем в первый день, и на 5 км больше, чем в третий. Сколько километров проходил турист каждый день? 5. Докажите, что при любых значениях переменных верно равенство (х - у) (х + у) – (a – х + у) (a – х - у) - а (2х – а) = 0. 6. На графике функции у = 3х + 8 найдите точку, абсцисса которой равна ее ординате. Критерии оценки: «5» - верно выполнены все задания; «4» - верно выполнены 5 заданий; «3» - верно выполнены 4 задания. ГЕОМЕТРИЯ Контрольная работа по теме: «Начальные геометрические сведения» Вариант 1 Три точки В, С и D лежат на одной прямой. Известно, что ВD = 17 см, DC = 25 см. Какой может быть длина отрезка ВС? Сумма вертикальных углов МОЕ и DOC, образованных при пересечении прямых МС и DЕ, равна 204°. Найдите угол МОD. С помощью транспортира начертите угол, равный 78°, и проведите биссектрису смежного с ним угла. Вариант 2 Три точки M, N и K лежат на одной прямой. Известно, что MN = 15 см, NK = 18 см. Каким может быть расстояние MK? Сумма вертикальных углов АОВ и СОD, образованных при пересечении прямых AD и ВС, равна 108°. Найдите угол ВОD. С помощью транспортира начертите угол, равный 132°, и проведите биссектрису одного из смежных с ним углов. Критерии оценки: «5» - верно выполнены все задания; «4» - выполнены 3 заданий, но есть ошибка; «3» - верно выполнены 2 задания. Контрольная работа по теме: «Треугольники» В 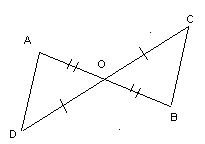 ариант 1 ариант 1На рисунке отрезки АВ и CD имеют общую середину О. Докажите, что 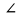 DAO = DAO =  CBO. CBO.Луч AD – биссектриса угла А. На сторонах угла А отмечены точки В и С так, что  ADВ = ADВ =  АDC. Докажите, что АВ = АС. АDC. Докажите, что АВ = АС.Начертите равнобедренный треугольник АВС с основанием ВС. С помощью циркуля и линейки проведите медиану ВВ1 к боковой стороне АС.  Вариант 2 На рисунке отрезки МЕ и PK точкой D делятся пополам. Докажите, что 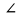 KMD = KMD = 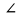 PED. PED.На сторонах угла D отмечены точки M и K так, что DM = DK. Точка Р лежит внутри угла D, и РК = РМ. Докажите, что луч DP – биссектриса угла МDК. Начертите равнобедренный треугольник АВС с основанием АС и острым углом В. С помощью циркуля и линейки проведите высоту из вершины угла А. Критерии оценки: «5» - верно выполнены все задания; «4» - выполнены 3 заданий, но есть ошибка; «3» - верно выполнены 2 задания. Контрольная работа по теме: «Параллельные прямые» Вариант 1 Отрезки EF и PQ пересекаются в их середине M. Докажите, что PE || QF. Отрезок DM – биссектриса треугольника СDЕ. Через точку М проведена прямая, параллельная стороне СD и пересекающая сторону DE в точке N. Найдите углы треугольника DMN, если 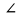 СDE = 68°. СDE = 68°.Вариант 2 Отрезки MN и EF пересекаются в их середине P. Докажите, что EN || MF. Отрезок AD – биссектриса треугольника ABC. Через точку D проведена прямая, параллельная стороне AB и пересекающая сторону AC в точке F. Найдите углы треугольника ADF, если 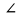 BAC = 72°. BAC = 72°.Критерии оценки: «5» - верно выполнены все задания; «4» - выполнены 2 задания, но есть ошибка; «3» - верно выполнено 1 задание. Контрольная работа по теме: «Соотношения между сторонами и углами треугольника» Вариант 1 На рисунке  ABE = 104°, ABE = 104°,  DCF = 76°, AC = 12 см. Найдите сторону АВ треугольника АВС. DCF = 76°, AC = 12 см. Найдите сторону АВ треугольника АВС.В треугольнике CDE точка М лежит на стороне СЕ, причем угол СМD острый. Докажите, что DE > DM. Периметр равнобедренного тупоугольного треугольника равен 45 см, а одна из его сторон больше другой на 9 см. Найдите стороны треугольника.  Вариант 2 На рисунке  BАE = 112°, BАE = 112°, 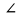 DВF = 68°, ВC = 9 см. Найдите сторону АС треугольника АВС. DВF = 68°, ВC = 9 см. Найдите сторону АС треугольника АВС.В треугольнике МNP точка K лежит на стороне MN, причем угол NKP острый. Докажите, что KP < MP. Одна из сторон тупоугольного равнобедренного треугольника на 17 см меньше другой. Найдите стороны этого треугольника, если его периметр равен 77 см. Критерии оценки: «5» - верно выполнены все задания; «4» - выполнены 3 задания, но есть ошибка; «3» - верно выполнены 2 задания. Контрольная работа по теме: «Прямоугольные треугольники» Вариант 1 1. В остроугольном треугольнике MNP биссектриса угла М пересекает высоту NK в точке О, причем ОК = 9 см. Найдите расстояние от точки О до прямой MN. 2. Постройте прямоугольный треугольник по гипотенузе и острому углу. 3. С помощью циркуля и линейки постройте угол, равный 150°. Вариант 2 1. В прямоугольном треугольнике DCE c прямым углом С проведена биссектриса EF, причем FC = 13 см. Найдите расстояние от точки F до прямой DE. 2. Постройте прямоугольный треугольник по катету и прилежащему к нему острому углу. 3. С помощью циркуля и линейки постройте угол, равный 105°. Критерии оценки: «5» - верно выполнены все задания; «4» - выполнены 3 задания, но есть ошибка; «3» - верно выполнены 2 задания. |
