Высшая математика.Элементы высшей алгебры и геометрии_ЭЭТбп_2201. Высшая математика
 Скачать 0.92 Mb.
|
 МИНИСТЕРСТВО НАУКИ И ВЫСШЕГО ОБРАЗОВАНИЯ РОССИЙСКОЙ ФЕДЕРАЦИИфедеральное государственное бюджетное образовательное учреждение высшего образования «Тольяттинский государственный университет»
Практическое задание №_1__ по учебному курсу Высшая математика.Элементы высшей алгебры и геометрии » (наименование учебного курса) Вариант 13,6,3 (при наличии)
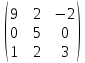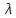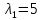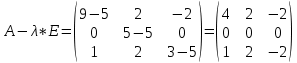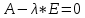Тольятти 2022_ РАЗДЕЛ № 1. ЛИНЕЙНАЯ АЛГЕБРА Задача 1. Определить собственные значения и собственные векторы матрицы третьего порядка.  Решение. 1) Найдем собственные числа из характеристического уравнения:   2) Для каждого  найдем его собственные вектора:   Тогда имеем однородную систему линейных уравнений, решим ее методом Гаусса:  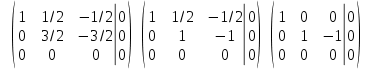 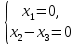 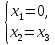 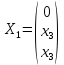 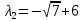  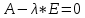Тогда имеем однородную систему линейных уравнений, решим ее методом Гаусса: 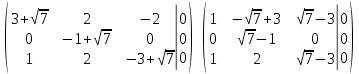 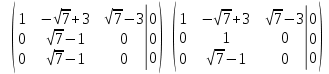 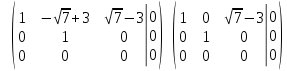   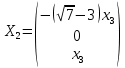 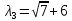  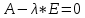Тогда имеем однородную систему линейных уравнений, решим ее методом Гаусса:   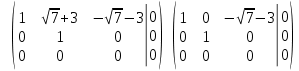 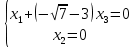 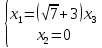 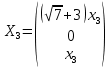 Задача 2. Доказать совместность системы и решить её тремя способами: по формулам Крамера, методом Гаусса и средствами матричного исчисления.  Решение. Исследуем систему на совместность. Воспользуемся теоремой Кронекера-Капелли, для этого найдем ранг расширенной матрицы системы и ранг матрицы системы. Найдем ранг матрицы методом элементарных преобразований. Ранг матрицы равен числу ненулевых строк в матрице после приведения её к ступенчатой форме при помощи элементарных преобразований над строками матрицы. 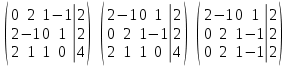 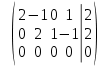 Ранг расширенной матрицы равен рангу матрицы системы, но меньше числа неизвестных. Система совместна и имеет бесконечно много решений. 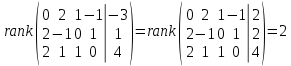 Данную систему можно решить только методом Гаусса: 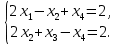  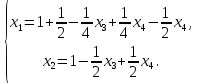 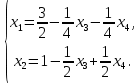 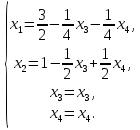 Задача 3. Исследовать и найти общее решение системы линейных однородных уравнений. 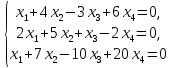 Решение. Приведем расширенную матрицу системы к ступенчатому виду:  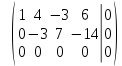 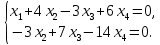   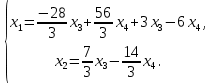 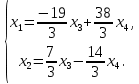 Общее решение имеет вид: 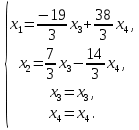 |