Задание. 5 занятие(2). Визуализация многомерных данных с помощью tsne
 Скачать 0.95 Mb. Скачать 0.95 Mb.
|
|
Визуализация многомерных данных с помощью t-SNE Целью уменьшения размерности является сохранение структуры многомерных данных в низкоразмерном пространстве. t-SNE (t-distributed stochastic neighbor embedding, стохастическое вложение соседей с t-распределением) относится к нелинейным методам уменьшения размерности для визуализации многомерных данных. Данный алгоритм относится к машинному обучению без учителя (unsupervised learning). Обучение без учителя означает отсутствие меток у данных, в отличии от обучения с учителем, где каждый объект имеет метку. Исходные данные – это объекты, которые находятся в многомерном пространстве. Задача – представить их в 2-х или 3-х мерном пространстве. Объекты, которые похожи друг на друга и находятся рядом друг с другом в многомерном пространстве, должны иметь аналогичную структуру и в пространстве меньшей размерности. t-SNE позволяет понять, на какое количество кластеров могут быть поделены данные, то есть этот метод не только визуализирует данные, но также и позволяет их исследовать. Основой t-SNE является SNE, представленный Хинтоном и Ровейсом в 2002 году. t-SNE имеет два важных отличия от SNE 2002 года: Используется симметричная версия SNE; Вместо нормального распределения используется распределение Стьюдента для вычисления расстояния в пространстве низкой размерности. 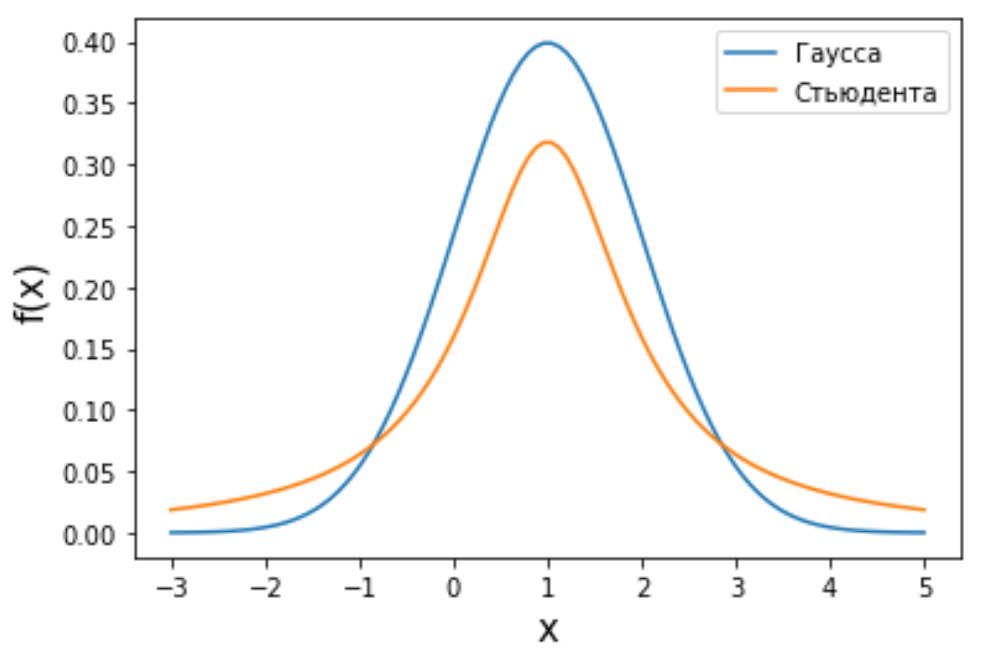 Рис. 1 В 2002 году появилось стохастическое вложение соседей (англ. Stochastic Neighbor Embedding, SNE) – это первая интерпретация изучаемого метода. Первый шаг алгоритма заключается в преобразовании многомерного евклидового расстояния между точками в условные вероятности, которые отражают сходство точек. Делается это по следующей формуле: 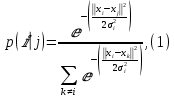 где 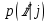 – это сходство двух объектов в пространстве высокой размерности; – это сходство двух объектов в пространстве высокой размерности;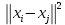 – евклидово расстояние между двумя векторами; – евклидово расстояние между двумя векторами;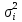 – дисперсия. – дисперсия.Норма 2, или Евклидова норма, или 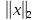 рассчитывается как рассчитывается как 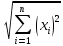 , где , где 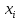 – это координаты вектора). – это координаты вектора).Сумма всех 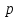 для одной точки равна 1. Значение для одной точки равна 1. Значение 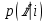 устанавливается равным нулю, так как необходима только попарная схожесть объектов. Если точки находятся близко друг к другу, то они считаются похожими и значение будет относительно высоким. Для каждой точки в пространстве рассчитывается ее похожесть со всеми остальными точками. устанавливается равным нулю, так как необходима только попарная схожесть объектов. Если точки находятся близко друг к другу, то они считаются похожими и значение будет относительно высоким. Для каждой точки в пространстве рассчитывается ее похожесть со всеми остальными точками. Не существует единственного значения дисперсии 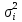 , которая центрируется над каждой многомерной точкой , которая центрируется над каждой многомерной точкой 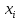 , для всех точек из набора данных. В плотных областях значение дисперсии меньше, чем для более разреженных областей. Дисперсии , для всех точек из набора данных. В плотных областях значение дисперсии меньше, чем для более разреженных областей. Дисперсии 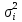 для каждой точки выбирается адаптивно с учетом фиксированного значения перплексии, которое задается пользователем. для каждой точки выбирается адаптивно с учетом фиксированного значения перплексии, которое задается пользователем. Параметр пeрплексии позволяет указать плотность точек для кластера (или же количество соседей). Пeрплексия описывает как далеко алгоритм собирается искать соседей в исходном многомерном пространстве, чтобы считать их принадлежащими одному и тому же множеству. Если установить это значение очень низким, то алгоритм будет пытаться разделить объекты на более мелкие кластеры в результирующем 2D-пространстве. Если значение слишком велико, то разные классы будут сгруппированы в одном кластере. Если параметр перплексии равен 30, то для 30 ближайших точек будут свои значения 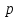 , как только выходим за предел 30 соседей, все становится равным 0. , как только выходим за предел 30 соседей, все становится равным 0.Если 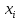 – это выброс, то расстояние от нее до других точек будет очень большим, следовательно, – это выброс, то расстояние от нее до других точек будет очень большим, следовательно, 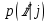 для такой точки будут чрезвычайно малы для всех j. В итоге получается, что функция стоимости будет почти нулевой для любого для такой точки будут чрезвычайно малы для всех j. В итоге получается, что функция стоимости будет почти нулевой для любого 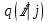 . Поэтому положение низкоразмерного аналога . Поэтому положение низкоразмерного аналога 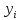 определялось бы очень неточно и не было бы особой разницы в том, где он расположен. Для решения этой проблемы был создал симметричный SNE. определялось бы очень неточно и не было бы особой разницы в том, где он расположен. Для решения этой проблемы был создал симметричный SNE.В симметричном SNE (Symmetric Stochastic Neighbor Embedding, Symmetric SNE) определяются совместные вероятности 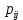 в многомерном пространстве как симметричные условные вероятности по формуле в многомерном пространстве как симметричные условные вероятности по формуле 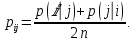 Это дает гарантию того, что 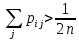 для всех точек 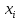 . В результате этого преобразования каждая точка данных . В результате этого преобразования каждая точка данных 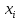 вносит значительный вклад в функцию стоимости. Так же теперь вносит значительный вклад в функцию стоимости. Так же теперь 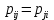 . .У точек 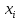 и и 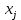 многомерного пространства есть аналоги многомерного пространства есть аналоги 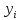 и и 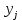 в пространстве низкой размерности. Для них также вероятность в пространстве низкой размерности. Для них также вероятность 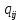 . . 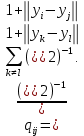 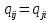 , а , а 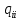 устанавливается равным нулю. устанавливается равным нулю. 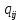 – это сходство двух объектов в пространстве низкой размерности. – это сходство двух объектов в пространстве низкой размерности.Второе отличие t-SNE от SNE – это использование t-распределения, которое имеет более широкие «хвосты» (Рис. 1). Сделано это для того, чтобы решить проблему скученности в пространстве низкой размерности. Если точки отображения 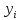 и и 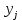 правильно моделируют сходство между точками данных высокой размерности правильно моделируют сходство между точками данных высокой размерности 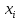 и и 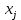 , условные вероятности , условные вероятности 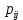 и и 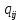 будут равны. t-SNE стремится найти низкоразмерное представление данных, которое минимизирует несоответствие между будут равны. t-SNE стремится найти низкоразмерное представление данных, которое минимизирует несоответствие между 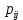 и и 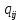 . .Функция стоимости данного метода – это расстояние Кульбака-Лейблера, которое рассчитывается по формуле 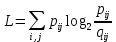 Если все 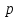 равны всем равны всем 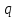 , то расстояние Кульбака-Лейблера (расстояние между плотностями распределения для каждой точки в пространстве) будет равно 0. Это то, к чему стремится алгоритм – минимизировать функцию стоимости с помощью метода градиентного спуска по отношению к , то расстояние Кульбака-Лейблера (расстояние между плотностями распределения для каждой точки в пространстве) будет равно 0. Это то, к чему стремится алгоритм – минимизировать функцию стоимости с помощью метода градиентного спуска по отношению к 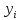 . Если . Если 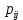 велико, то нужно большое значение для велико, то нужно большое значение для 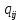 . Если . Если 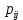 мало, то мало, то 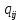 должно иметь тоже низкое значение для представления точек, которые находятся далеко друг от друга. должно иметь тоже низкое значение для представления точек, которые находятся далеко друг от друга.Градиент функции стоимости выглядит следующим образом: 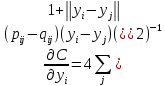 Точки пространстве низкой размерности генерируются случайным образом. Затем, с помощью градиентного спуска, идет поиск оптимальных точек 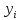 , чтобы функция стоимости была минимальна. А будет она минимальна тогда, когда , чтобы функция стоимости была минимальна. А будет она минимальна тогда, когда  и и 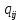 будут равны, то есть структура данных в пространстве с высокой размерностью будет аналогична структуре данных в пространстве с низкой размерностью. будут равны, то есть структура данных в пространстве с высокой размерностью будет аналогична структуре данных в пространстве с низкой размерностью.Рассмотрим использование t-SNE на примере набора данных, который содержит 16 признаков для описания животных из зоопарка, а также классы, к которым эти животные относятся: млекопитающие, птицы, рептилии, рыбы, амфибии, насекомые и беспозвоночные.   Перед тем, как данные визуализировать, удалим из датафрейма столбцы animal_name и class_type и проведем нормализацию данных.  Далее представлен пример визуализации с использованием библиотеки sklearn.  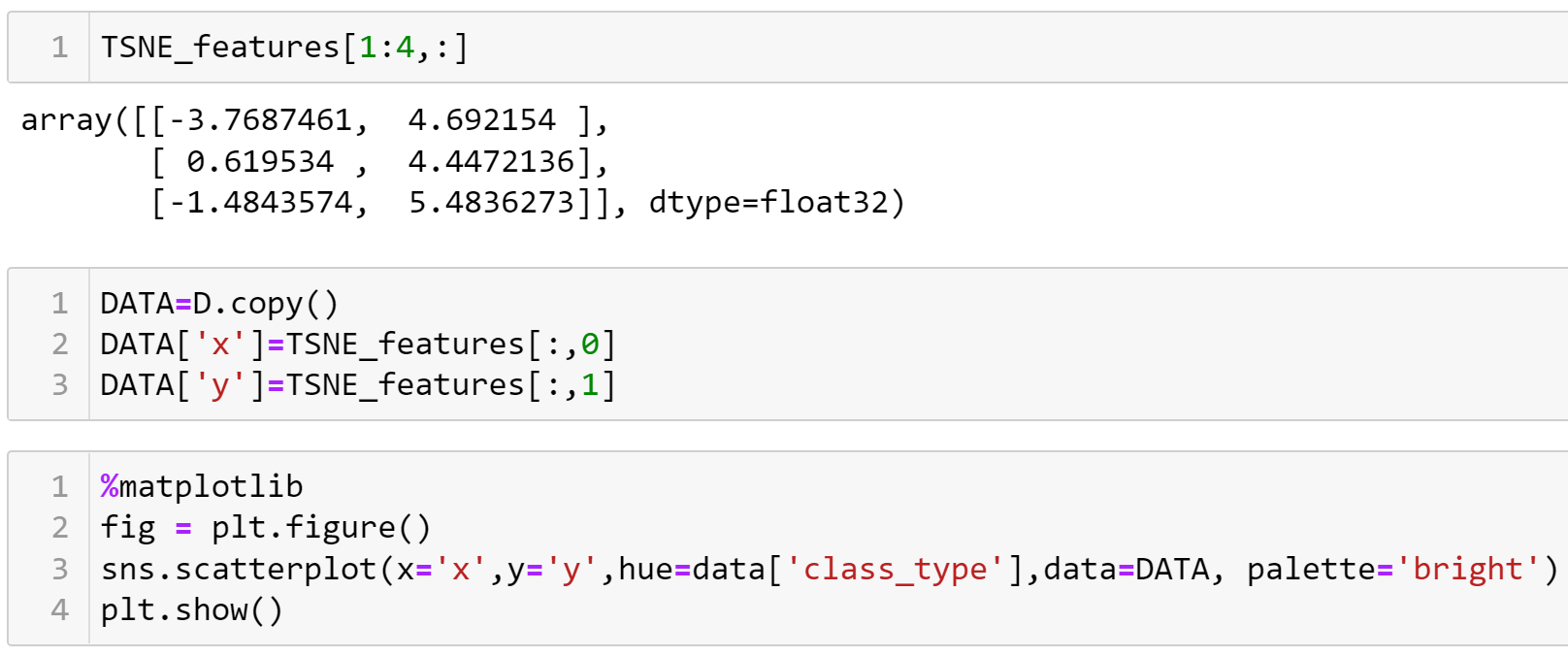 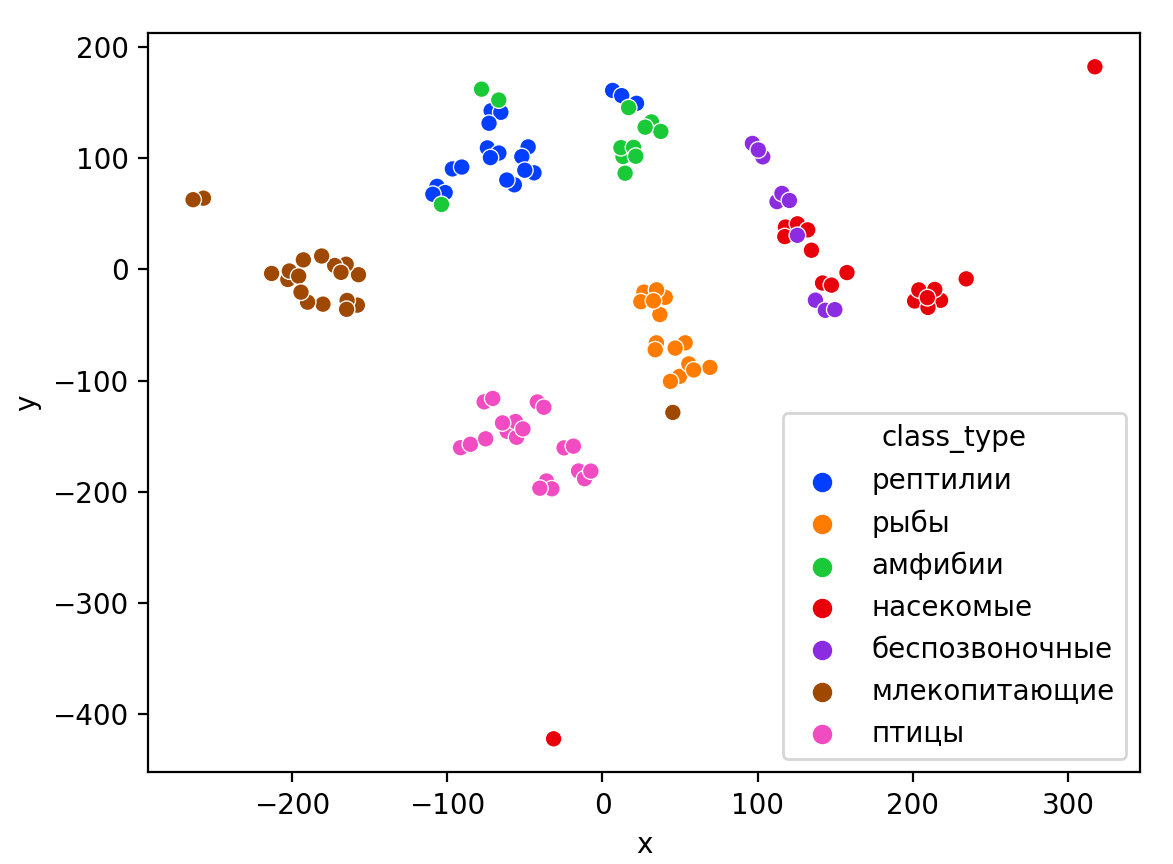 perplexity=5 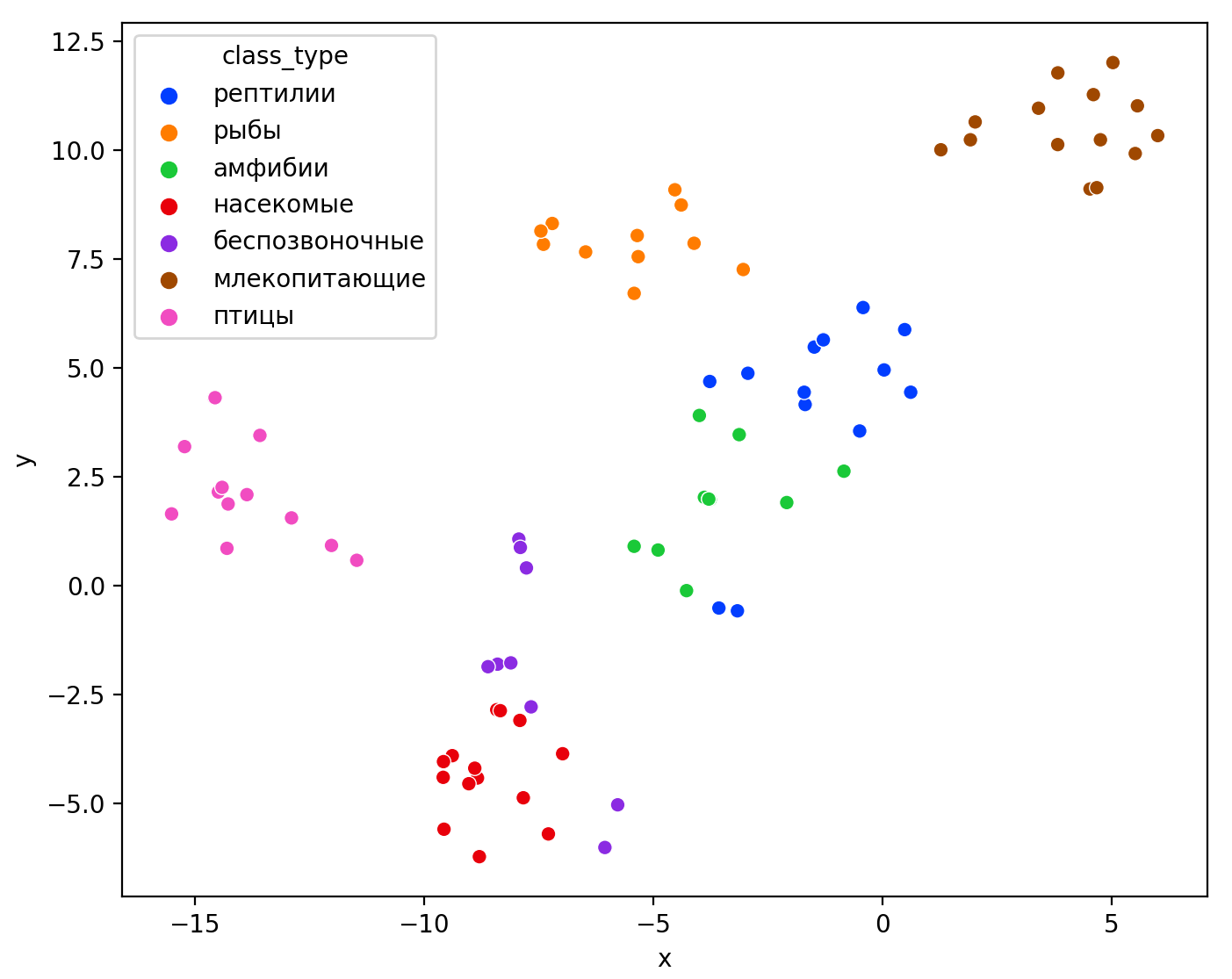 perplexity=25 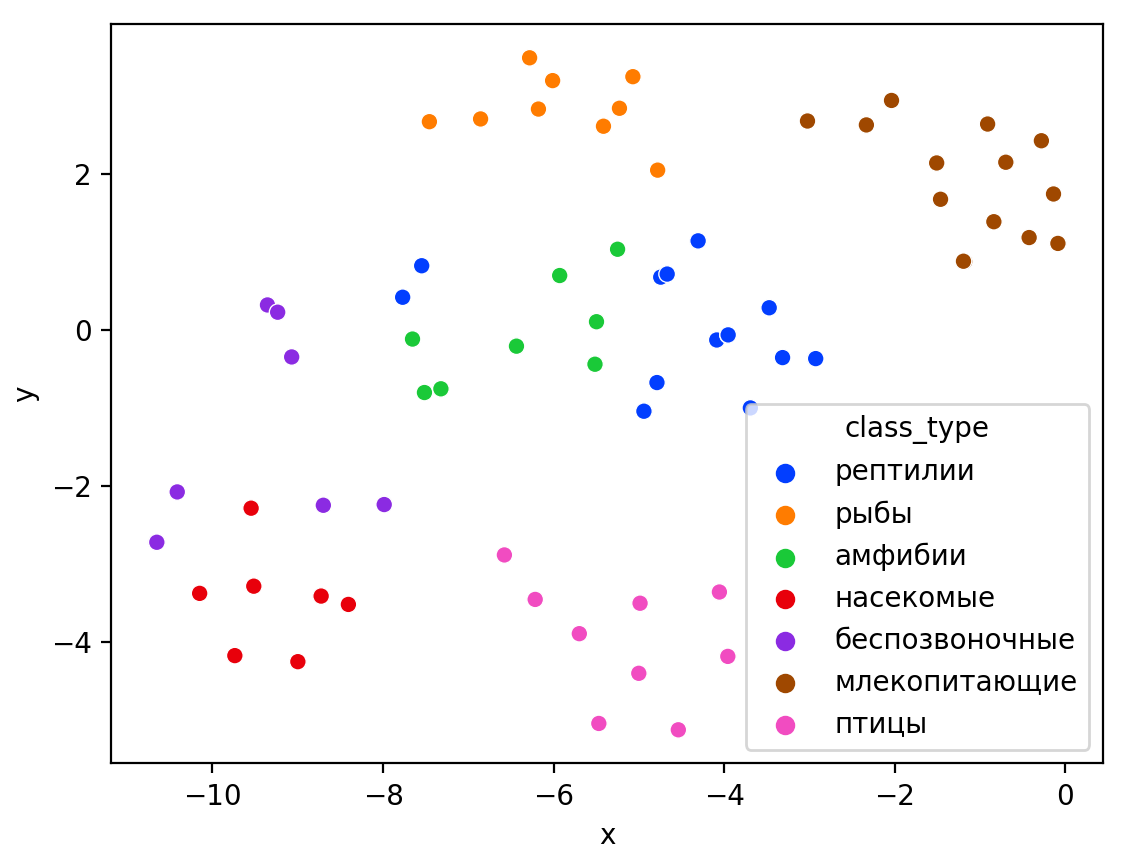 perplexity=50 В результате визуализации видим, что явно выделены кластеры для млекопитающих, рыб и птиц. Насекомые находятся рядом с беспозвоночными, а амфибии с рептилиями. Если добавить в исходный набор новые данные, то результат будет совершено иным, так как плотности распределений будут изменены и расстояние Кульбака-Лейблера, соответственно, тоже. t-SNE – это случайный процесс, поэтому в зависимости от инициализации генератора случайных чисел получаются разные результаты, поэтому необходимо зафиксировать генератор. Сегменты, которые визуализируются с помощью данного алгоритма, могут немного перемешиваться друг с другом, это связано с тем, что объекты очень похожи друг на друга и, соответственно, в многомерном пространстве расположены близко друг к другу. Визуализация многомерных данных с помощью UMAP UMAP (Uniform Manifold Approximation and Projection, равномерная аппроксимация многообразия) – алгоритм машинного обучения без учителя, который позволяет визуализировать многомерные данные, путем нелинейного снижения размерности. Лиланд Макиннес, Джон Хили и Джеймс Мелвилл, авторы алгоритма, считают, что UMAP намного быстрее и более вычислительно эффективный, чем t-SNE, а также лучше справляется с задачей переноса глобальной структуры данных в новое, уменьшенное пространство. Алгоритм имеет достаточно сложное математическое обоснование, поэтому кратко рассмотрим принцип работы UMAP. UMAP состоит из двух этапов: построение многомерного графа и сопоставление ему графа из пространства низкой размерности. Первый шаг – это расчет расстояния между всеми исследуемыми объектами с помощью некоторой метрики. Это может быть евклидово расстояние, манхэттенское расстояние или, например, косинусное расстояние, с помощью которого можно исследовать текстовые данные. Далее для каждого объекта определяется список его k ближайших соседей и строится взвешенный граф для соседей. Далее создается новый граф в пространстве низкой размерности и его ребра приближаются к исходному. Для этого минимизируется расстояние Кульбака-Лейблера для каждого ребра графа из исходного и низкоразмерного пространства. Основные параметры, которые необходимо задать для работы алгоритма: n_components – размерность итогового пространства (по умолчанию 2); n_neighbors – количество соседей, которые рассматриваются для каждого объекта (по умолчанию 15). Если это значение мало, то будут рассматриваться самые ближайшие соседи и это приведет к большому количеству кластеров, если же это значение велико, то будет хорошо сохранена глобальная структура, но более мелкие детали будут потеряны min_dist – минимальное расстояние между точками в малых измерениях (по умолчанию 0.1), очень низкие значения приведут к более плотным кластерам, а высокие значения препятствуют объединению точек; metric – это название формулы вычисления расстояния между точками. (по умолчанию euclidean). Рассмотрим использование UMAP на том же примере.  Далее представлен пример визуализации с использованием библиотеки umap-learn (для установки используйте в командной строке pip install umap-learn) для различных параметров.  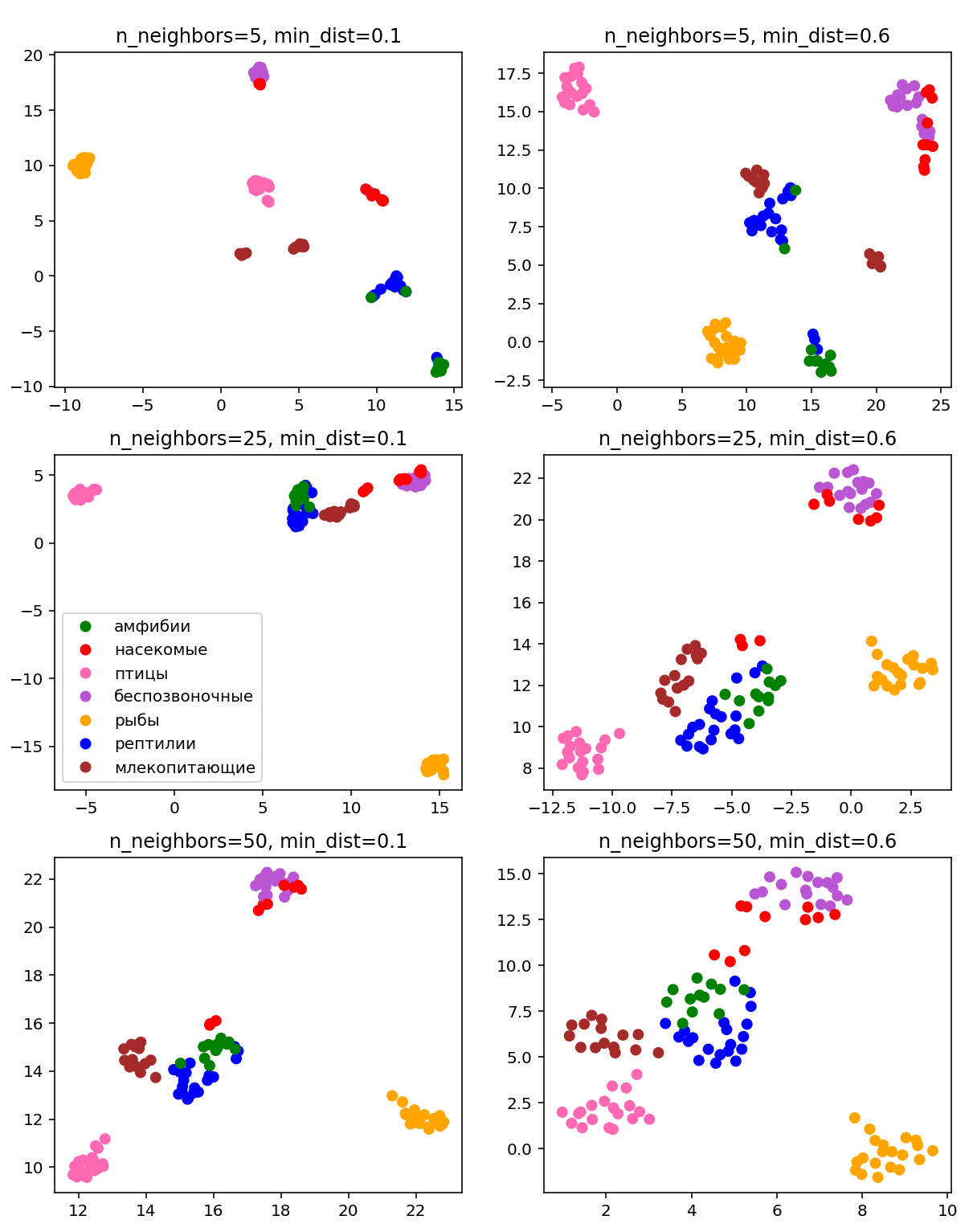 С помощью UMAP получили результат, очень похожий на то, что дает t-SNE. Практическое задание Выполнить визуализацию многомерных данных, используя t-SNE. Необходимо использовать набор данных MNIST или fashion MNIST (можно использовать и другие готовые наборы данных, где можно наблюдать разделение объектов по кластерам). Рассмотреть результаты визуализации для разных значений перплексии. Выполнить визуализацию многомерных данных, используя UMAP с различными параметрами n_neighbors и min_dist. Рассчитать время работы алгоритма с помощью библиотеки time и сравнить его с временем работы t-SNE. Оформить отчет о проделанной работе. Отчет должен содержать результаты визуализации для разных значений параметров и выводы. |
