контрольная работа по Физике Земли и атмосферы. Влияние нейтральной атмосферы на результаты геодезических измерений физика земли и атмосферы

• Название: Влияние нейтральной атмосферы на результаты геодезических измерений физика земли и атмосферы
• Анкор: контрольная работа по Физике Земли и атмосферы
• Дата: 17.08.2022
• Размер: 38.78 Kb.
• Имя файла: dlia_64p-213_11149232.docx
• Тип: Задача; #647260

Задание контрольной работы № 1

ВЛИЯНИЕ НЕЙТРАЛЬНОЙ АТМОСФЕРЫ

НА РЕЗУЛЬТАТЫ ГЕОДЕЗИЧЕСКИХ ИЗМЕРЕНИЙ

ФИЗИКА ЗЕМЛИ И АТМОСФЕРЫ

ФИО студента и номер группы

Вариант 13.

Исходные данные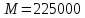











Линейные измерения

Задача 1. С какой средней квадратической ошибкой m_n следует определять показатель преломления, если расстояние D требуется измерить с относительной ошибкой 1/M, а измерения выполняют светодальномером.

Дано: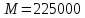





Решение: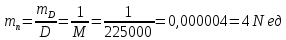



Вывод: для определения расстояния с относительной ошибкой 1/225000 показатель преломления должен быть известен с точностью до миллионных долей (до 4 N-ед).

Задача 2. В условиях предыдущей задачи оценить требования к точности измерения температуры m_T, давления m_p и влажности m_e воздуха, если измерения выполнены светодальномером.

Дано: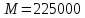





Решение:

Согласно выводам, полученным при решении Задачи 1, для измерения расстояния с точностью 1/225000 показатель преломления следует определять с точностью 4 N-ед., т.е.:



Воспользуемся принципом равных влияний:



Тогда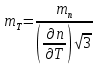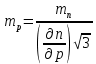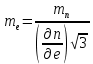



Подставив в формулы значение средней квадратической ошибки показателя преломления, полученное при решении Задачи 1, и частные производные для светового диапазона (Таблица 1 методических указаний), получим: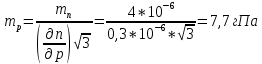







Вывод: при измерении расстояний светодальномером с относительной ошибкой 1/225000 температуру, давление и влажность следует определять с точностью 2,31 К, 7,7гПа и 57,7гПа, соответственно.

Задача 3. К какой ошибке Δ_D определения расстояния D приведет неучет изменения температуры на ΔT, если значения других метеопараметров были постоянными, т.е. Δp=Δe=0. Измерения выполнены светодальномером.

Дано:





Решение:

Характер влияния изменений 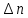показателя преломления на измеренную дальность D имеет вид:



По условию зменение метеопараметров ведет к изменению показателя преломления: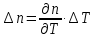



Частная производная для светового диапазона задана в таблице 1 методички:



Итак,



Вывод: неучет изменения температуры на ΔT приведет к ошибке Δ_D определения расстояния D равной 0,0144м.

Задача 4. Сравнить ошибки определения расстояния D свето- Δ_Dсв и радиодальномером Δ_Dрадио, обусловленные неучетом влияния влажности, если на момент измерений на высоте измерений абсолютная влажность была равна e=Δe.

Дано:





Решение:

Характер влияния изменений 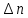показателя преломления на измеренную дальность D имеет вид: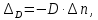



где



Итак,


Для светового диапазона:


поэтому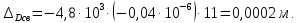



Для радио диапазона: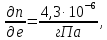


поэтому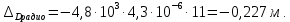



Вывод: при неучете влияния влажности ошибки измерения расстояния свето- и радиодальномерами составляют и 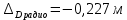соответственно.

Угловые измерения

Задача 5. К какой ошибке определения превышения Δ_h приведет угол вертикальной рефракции r=10״ на трассе протяженностью D, если измеренное зенитное расстояние равно z? Считать, что ошибка определения зенитного расстояния Δ_Z=r, а точность определения превышения зависит только от точности угловых измерений. Сравнить полученное значение с предельной случайной средней квадратической ошибкой нивелирования I, II, III и IV классов. (предельную ошибку принять равной утроенной случайной средней квадратической ошибке (Таблица 8.2)). Сделать вывод о соответствии полученной точности требованиям инструкции по геометрическому нивелированию.

Таблица 8.2 – Точность нивелирования I, II, III и IV классов

Класс нивелирования	Случайная средняя квадратическая ошибка, мм/км
I	0,8
II	2,0
III	5,0
IV	10,0

Дано:





Решение:



Сравним полученное значение с предельной случайной средней квадратической ошибкой нивелирования I, II, III и IV классов:

для I класса: 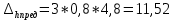, тогда

для II класса: , тогда

для III класс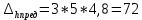а: , тогда

для IV класс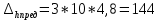а: , тогда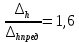

Вывод: угол вертикальной рефракции r=10” приведет ошибке определения превышения Δ_h =-230мм.

Задача 6. В условиях предыдущей задачи определить соответствующее значение вертикального градиента показателя преломления.

Дано:





Решение:

Вертикальный градиент показателя преломления



Вывод: вертикальный градиент показателя преломления для угла вертикальной рефракции r=10״равен .

Задача 7. Используя исходные данные Задачи 5 и результаты, полученные в Задаче 6, вычислить вертикальный градиент температуры, который мог привести к формированию угла рефракции r, если градиент давления равен его нормальному значению 0,12 гПа/м, а градиент влажности пренебрежимо мал.

Дано:





Решение: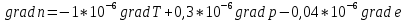



так как градиент влажности пренебрежимо мал, то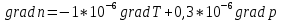



выразим и вычислим градиент температуры



Вывод: градиент температуры, который мог привести к формированию угла рефракции r равен .

Задача 8. Вычислить углы горизонтальной рефракции для визирных линий длиной D, расположенных на расстояниях 0,5; 1,0 и 3,0 м от нагретой бетонной стены, если горизонтальные температурные градиенты равны



а горизонтальные градиенты давления и влажности пренебрежимо малы. На каком расстоянии от стены (из трех указанных выше) следует располагать визирную линию, если измерения выполняют в полигонометрии IV класса (предельная ошибка угловых измерений – 5״)?

Дано:



Решение: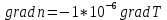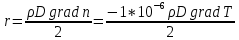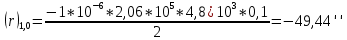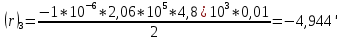











Вывод: если измерения выполняют в полигонометрии IV класса, то визирную линию следует располагать на расстоянии от стены 3,0м.

Задание контрольной работы № 2

МЕТОДЫ УЧЕТА ВЛИЯНИЯ АТМОСФЕРЫ НА РЕЗУЛЬТАТЫ ГЕОДЕЗИЧЕСКИХ ИЗМЕРЕНИЙ

ФИЗИКА ЗЕМЛИ И АТМОСФЕРЫ

ФИО студента и номер группы

Вариант 13.

Исходные данные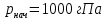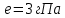















Задача 1. Вычислить поправку h_r в превышение за влияние вертикальной рефракции, если превышение измерено методом тригонометрического нивелирования на трассе протяженностью D (наклонная дальность), а фактический коэффициент рефракции равен k_факт, средний радиус кривизны земного сфероида принять равным 6371 км.

Дано: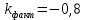







Решение:



Вывод: поправка h_r в превышение за влияние вертикальной рефракции составляет (+1450)мм.

Задача 2. В условиях предыдущей задачи вычислить ошибку _hr определения поправки за рефракцию, если при вычислениях использовали стандартный коэффициент рефракции, равный +0,14. Сравнить полученное значение с предельной случайной средней квадратической ошибкой нивелирования I, II, III и IV классов (Таблица 8.2). Сделать вывод о соответствии полученной точности требованиям Инструкции по геометрическому нивелированию

Таблица 8.2 – Точность нивелирования I, II, III и IV классов

Класс нивелирования	Случайная средняя квадратическая ошибка, мм/км
I	0,8
II	2,0
III	5,0
IV	10,0

Дано:







Решение:





Согласно инструкции случайная средняя квадратическая ошибка определения превышения в нивелирном ходе I класса – 0,8 мм/км.

Предельная случайная средняя квадратическая ошибка с учетом расстояния 4,8 км равна: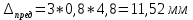



Ошибка, обусловленная использованием стандартного коэффициента рефракции, в данном случае превысила допустимое значение в 148 раз.

Согласно инструкции случайная средняя квадратическая ошибка определения превышения в нивелирном ходе II класса – 2 мм/км.

Предельная случайная средняя квадратическая ошибка с учетом расстояния 4,8 км равна: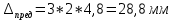



Ошибка, обусловленная использованием стандартного коэффициента рефракции, в данном случае превысила допустимое значение в 59 раз.

Согласно инструкции случайная средняя квадратическая ошибка определения превышения в нивелирном ходе III класса – 5 мм/км.

Предельная случайная средняя квадратическая ошибка с учетом расстояния 0,9 км равна:



Ошибка, обусловленная использованием стандартного коэффициента рефракции, в данном случае превысила допустимое значение в 24 раза.

Согласно инструкции случайная средняя квадратическая ошибка определения превышения в нивелирном ходе IV класса – 10 мм/км.

Предельная случайная средняя квадратическая ошибка с учетом расстояния 0,9 км равна: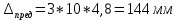



Ошибка, обусловленная использованием стандартного коэффициента рефракции, в данном случае превысила допустимое значение в 12 раз.

Вывод: ошибка, обусловленная использованием стандартного коэффициента рефракции, превышает допустимые значения для всех классов нивелирования.

Задача 3. В условиях Задачи 1 вычислить значения вертикальных градиентов показателя преломления grad_срn и температуры grad_срT, которые могли сформировать такое значение k_факт. Градиент давления считать равным его нормальному значению 0,12 гПа/м.

Дано: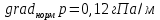







Решение:

Воспользуемся формулой для определения градиента показателя преломления grad_срn, как



Тогда grad_срT выразим и вычислим из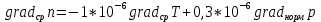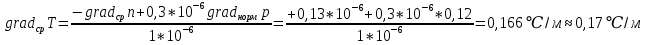





Вывод: значения вертикальных градиентов показателя преломления grad_срn и температуры grad_срT соответственно равны 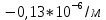и .

Задача 4. Вычислить поправку Δ_D в измеренную наклонную дальность D, если температура и давление в точке стояния прибора равны t_нач и p_нач. Для определения индекса преломления использовать формулу (5).



Дано: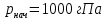







Решение:

Вычислим нормальный N_норм и фактический N индексы преломления: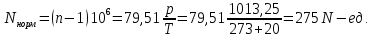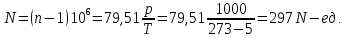





Поправка за отличие температуры и давления от нормальных условий:



Поправка в измеренное расстояние:



Вывод: поправка Δ_D равна -105,6 мм

Задача 5. Показатель преломления вычисляли, используя температуру t_нач и давление p_нач, измеренные на высоте 1,5 м встроенными в электронный тахеометр датчиками. Между тем, в среднем траектория длиной D проходила на высоте 20 м над подстилающей поверхностью. Вычислить ошибку в измеренном расстоянии Δ_D, если средние для слоя (1,5-20) м значения градиентов температуры и давления равны grad_верT = - 0,1⁰/м; grad_верр = 0,12 гПа/м. Влиянием влажности пренебречь.

Примечание. Изменение температуры ΔT и давления Δp c высотой вычислить, используя их вертикальные градиенты и разность высот: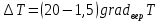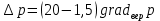





Дано: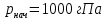







Решение:

Вычислим N_нач и N_конеч индексы преломления:





Поправка за отличие температуры и давления от нормальных условий:



Поправка в измеренное расстояние: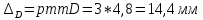



Вывод: поправка Δ_D равна 14,4мм

Задача 6. Используя модель Хопфилд, вычислить значение тропосферной задержки d_троп для спутника, расположенного на высоте α над горизонтом, если температура и давление в точке расположения спутникового приемника равны t_нач и p_нач, а влиянием влажной составляющей тропосферной задержки пренебрегли.

Дано: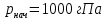









Решение:

Вычислим высоту тропосферы для сухой составляющей показателя преломления:



Сухая составляющая зенитной тропосферной задержки равна:



Полная тропосферная задержка с учетом высоты спутника:



Вывод: значение тропосферной задержки d_троп составляет 2,426м.

Задача 7. В условиях предыдущей задачи оценить ошибку определения псевдодальности Δ_d, обусловленную пренебрежением влажной составляющей тропосферной задержки, если абсолютная влажность в точке расположения спутникового приемника равна e.

Дано: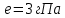









Решение:

Высоту тропосферы H_в для влажной составляющей показателя преломления принимают равной 11000 м (нижний слой атмосферы, в котором сосредоточена основная масса атмосферной влаги).

Тогда влажная составляющая зенитной тропосферной задержки равна:



Полная тропосферная задержка с учетом влажной составляющей:



Ошибка определения псевдодальности: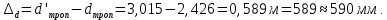

Вывод: