лекция обработки мат результатов. Лекция Матем обработка. Лекци Элементы математической обработке результатов геодезических измерений
 Скачать 180.53 Kb. Скачать 180.53 Kb.
|
Лекция3.Элементы математической обработке результатов геодезических измерений3.1. Понятие о геодезических измерениях 3.2. Погрешности геодезических измерений 3.3. Критерии оценки точности 3.4. Нормальное распределение 3.5. Предельная погрешность.Оценка точности равноточныхизмерений. 3.6. Оценка точности неравноточныхизмерений. 3. 1.Понятие о геодезических измеренияхПроцесс производства геодезических работ включает полевые измерения, составляющие основную часть геодезических работи камеральную обработку измеренных величин в соответствии с установленными математическими правилами и стандартами. Под измерениями в принципе понимают качественное сравнение двух физических величин, из которых одна является единицей меры и известна с достаточной точностью. Строго говоря, абсолютно неизменных величин в природе не существует. Однако практически многие величины в процессе геодезических измерений можно считать неизменными, например расстояния и углы на местности между геодезическими пунктами, образующие основное содержание полевых геодезических измерений. Для производства измерений необходимы: объект измерения, инструменты (приборы), исполнитель, определенная естественная среда, метод измерения и другие менее значительные факторы. Совокупность этих факторов и образует условия процесса геодезических измерений. С точки зрения условий их выполнения геодезические измерения разделяют на равноточные и неравноточные. Равноточными измерениями считают такие, которые производят одним и тем же инструментом или им подобным по точности прибором, одним и тем же (либо аналогичным) методом и в аналогичных условиях. В тех случаях, когда нарушаются эти условия, результаты таких измерений называются неравноточными. По классу точности результатов измерений их разделяют на высокоточные технические. Измерения, которые необходимо выполнить, чтобы получить только по одному значению каждой искомой величины, называют необходимыми. Измерения сверх необходимых называют избыточными. Понятие «избыточные измерения» не следует смешивать с понятием «излишнее измерение». Избыточные измерения в геодезии являются обязательными. Они позволяют выявлять возможные промахи и просчеты, а также дают возможность судить о точности измерений и повышать точность окончательных результатов проведенных измерений. 3. 2.Погрешности геодезических измеренийСуществование истинного или приближенного к действительному значения измеряемой величины х считается неотъемлемым условием любого измерения. Результаты измерений l как правило, отличаются от истинного значения величины х на величину ∆х. Математически это можно выразить следующим образом: ∆х = li – х, где ∆х – истинная величина погрешности измерения. Погрешность – отступления от истинного значения, порождаемые различными факторами. Их можно подразделить на приборные, личные, внешние и методические. Приборные погрешности обусловлены несовершенством технических средств измерения. Личные погрешности определяются индивидуальными особенностями и квалификацией исполнителя. Внешние- связаны с изменениями внешней среды (температуры, давления, влажности и рядом других). Методические погрешности зависят от применяемого способа измерения, тщательности и строгости учета условий измерений. При рассмотрении элементарных погрешностей речь не может идти о грубых (промахи либо просчеты) и систематических ошибках. Просчеты, как правило, исключаются из измерений путем повторных либо многократных измерений. Систематическиепогрешности можно исключить путем введения поправок, если они известны. Во всяких измерениях систематические погрешностидолжны быть изучены и по возможности исключены из результатов измерений. Возникновение и действия систематических ошибок зависят от видов и способов измерений, поэтому изучение их происхождения является задачей научных дисциплин, в которых рассматриваются такие измерения. В дальнейшем изложении при математической обработке результатов равноточных и неравноточных измерений будут рассматриваться только неизбежные случайные погрешности, влияние которых может быть установлено с достаточной определенностью. К таким погрешностям относят неточность мерных приборов и инструментов, способы измерений, многократность измерений и др. Такие обстоятельства, как, например, опытность измеряющего, прозрачность атмосферы и подобные им причины, влияние которых на результаты измерений не может быть установлено с достаточной определенностью, учитываются только при организации и производстве измерений. Свойства случайных погрешностей: 1. Случайные погрешности не превосходят определенный предел, называемый предельной погрешностью. Если получившийся результат больше, то это грубая погрешность. Математически это можно записать так: 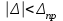 , где , где 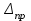 – предельная погрешность. – предельная погрешность.2.Вероятность получения положительной и отрицательной погрешности одинакова. Благодаря этому свойству можно выделить систематическую погрешность, так как она во всех результатах одного знака. Математически это свойство выглядит так: 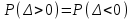 . .3. Чем больше абсолютная величина погрешности, тем реже она встречается. 4. Свойство компенсации. При бесконечном количестве измерений случайные погрешности компенсируют друг друга, то есть в сумме дают 0. То есть: 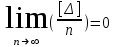 . .Таким образом, из последнего свойства следует, что при большом количестве измерений наиболее близкий к истинному результат можно получить, взяв среднее арифметическое из всех полученных результатов. При бесконечном количестве измерений это будет истинным значением измеряемой величины. Это среднее арифметическое называется арифметической срединой: 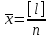 , где , где 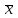 – средняя арифметическая средина, l – результат измерения, а n – количество измерений. – средняя арифметическая средина, l – результат измерения, а n – количество измерений.3. 3.Критерии оценки точностиПод критерием понимается признак или совокупность признаков по которым принимается решение. Существует множество критериев оценки точности измерений. Основные из них: средняя квадратическая, погрешности средняя погрешности , срединная погрешности. Самая часто используемая – это средняя квадратическая погрешности. Существует несколько формул ее вычисления. По формуле Гаусса средняя квадратическая погрешности вычисляется как: 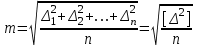 , где m – средняя квадратическая ошибка. Однако, для того, чтобы вычислить среднюю квадратическую погрешность по этой формуле, необходимо знать истинное значение величины, для определения , где m – средняя квадратическая ошибка. Однако, для того, чтобы вычислить среднюю квадратическую погрешность по этой формуле, необходимо знать истинное значение величины, для определения 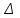 . Так как истинное значение величины известно довольно редко, то чаще пользуются другой формулой, формулой Бесселя: . Так как истинное значение величины известно довольно редко, то чаще пользуются другой формулой, формулой Бесселя: 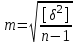 , где δ – отклонение от средней арифметической средины. , где δ – отклонение от средней арифметической средины.Также можно посчитать среднюю квадратическую ошибку арифметической средины. Она обозначается M и вычисляется по формуле: 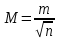 , то есть средняя квадратическая ошибка арифметической средины в , то есть средняя квадратическая ошибка арифметической средины в 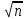 раз меньше средней квадратической погрешности измерения. Таким образом, чем больше n, тем ближе арифметическая средина к истинному значению величины. раз меньше средней квадратической погрешности измерения. Таким образом, чем больше n, тем ближе арифметическая средина к истинному значению величины.Средняя погрешности характеризует абсолютные значения истинных ошибок. Она вычисляется по формуле: 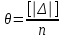 , где , где 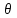 – средняя ошибка, а – средняя ошибка, а 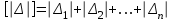 . .Срединная ошибка – число, вероятность появления погрешности больше или меньше которого равна. То есть: 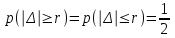 , где r – срединная погрешности , где r – срединная погрешностиВсе погрешности , рассматриваемые до этого – абсолютные. Они используются для определения точности измерения углов. Для точности измерения расстояний используются относительные погрешности. Относительная погрешность – дробь, в числителе которой стоит 1. Таким образом, для расстояний будет относительная средняя квадратическая ошибка, относительная средняя ошибка, относительная срединная ошибка. Пример: Даны результаты измерений угла: в треугольнике 179 59,8' 180 00,3', 179 59,1' 180 00,7' 180,01' Определить среднюю квадратическую и среднюю погрешности Решение: 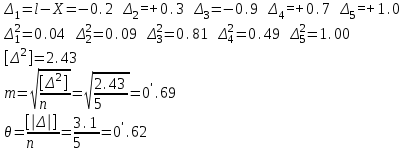 Даны результаты измерений угла: 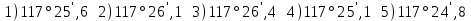 . Определить среднюю квадратическую ошибку. . Определить среднюю квадратическую ошибку.Решение: 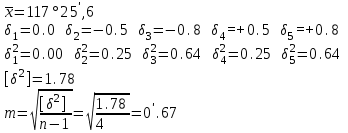 3. 4.Нормальное распределениеВеличину и знак случайной ошибки нельзя предсказать заранее, однако можно указать приближенные значения, среди которых будет ошибка. Доказано, что случайные ошибки, как и большинство случайных величин, подчиняется нормальному закону распределения. Графически, этот закон можно представить как кривую Гаусса, или кривую ошибок – рис. 37. 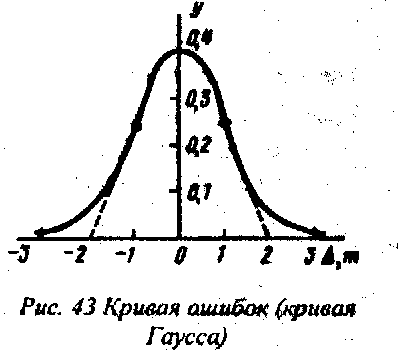 Рис.37. Кривая Гаусса Рис.37. Кривая ГауссаЕсли на оси абсцисс отложить величины случайных ошибок Δ, а по оси ординат – их число(φ(Δ) – плотность нормального распределения ошибки), то получим кривую ошибок, или кривую Гаусса. Уравнение кривой имеет вид: 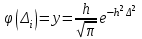 (1) (1)где 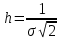 – мера точности; – мера точности;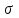 – среднее квадратическое отклонение. – среднее квадратическое отклонение.Если формула (1) получена по результатам измерений, то 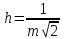 , где m – средняя квадратическая ошибка. , где m – средняя квадратическая ошибка.Принимая, вместоdm(1) получим: 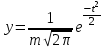 (2). (2).Пример. Построить кривую нормального распределения, если Δ=0, m, 2m, 3m; m=1,00''. Решение. Подставляв формулу (22) m=1,00'', получаем 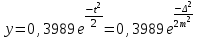 ,Приведенным значениям Δ и m соответствуют данные табл.2 ,Приведенным значениям Δ и m соответствуют данные табл.2Таблица 2. Результатырасчетов по определению исходных данных, для построениякривой нормального распределения.  Построенная по значениям Δ и y кривая(см. рис. 37) имеет следующие свойства: расположенана оси абсцисс, так как не имеет значений 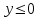 ; ;симметрична относительно оси oy; при Δ=0 величина y принимает максимальное значение; имеет точки перегиба при Δ = ± m; касательные к кривой в точках перегиба пересекаются с осью абсцисс в точках ± 2m. 3. 5. Предельная погрешность Оценка точности. равноточныхизмеренийБлагодаря практическим опытам было доказано, что абсолютное большинство случайных погрешностей (68,3%) данного ряда измерений находится в интервале от 0 до 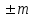 , в интервале от 0 до , в интервале от 0 до 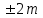 – 95,4%, а от 0 до – 95,4%, а от 0 до 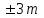 - 99,7% измерений. - 99,7% измерений.На основании этого за предельную погрешность 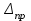 принимают утроенную среднюю квадратическую погрешность: принимают утроенную среднюю квадратическую погрешность: 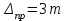 . Иногда, для повышения точности, принимают . Иногда, для повышения точности, принимают 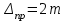 . Погрешности измерений, превосходящих . Погрешности измерений, превосходящих 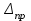 считают грубыми. считают грубыми.Равноточные измерения – измерения, выполненные при одинаковых условиях. Также, равноточные измерения можно определить, как измерения, средние квадратические ошибки которых равны. То есть: 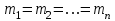 . .Для повышения точности, иногда, одну и ту же величину измеряют несколько раз. Двойные измерения – измерения одной и той же величины дважды. Двойные равноточные измерения – двойные измерения, выполненные при одинаковых условиях. При двойных равноточных измерениях, для определения средней квадратической ошибки, берут не сами измерения, как в предыдущем случае, а разности измерений d. То есть если при первых измерения были получены результаты 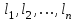 , а при вторых – , а при вторых – 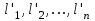 , то разность d, берется: , то разность d, берется: 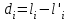 . .В таком случае, средняя квадратическая ошибка будет 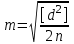 , а средняя квадратическая ошибка двух измерений – , а средняя квадратическая ошибка двух измерений – 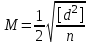 . .Пример: Даны результаты измерения угла: 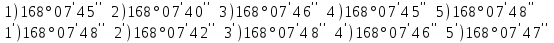 Найти среднюю квадратическую ошибку. 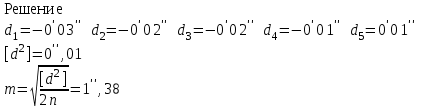 Даны результаты измерения длины линии. 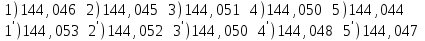 Определить среднюю квадратическую ошибку. 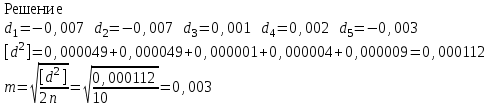 Даны результаты определения превышений между двумя реперами. 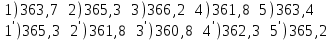 Определить среднюю квадратическую ошибку измерения, наиболее надежное значение превышения и его среднюю квадратичекую ошибку. 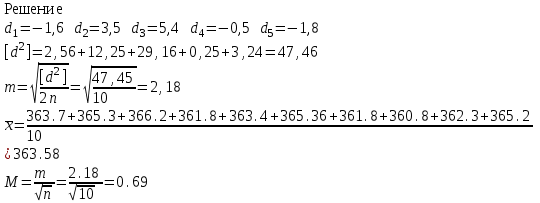 3. 6.Оценка точности неравноточныхизмеренийНеравноточные измерения – измерения, выполненные при разных условиях. Например, техническим и точным теодолитом. Также неравноточные измерения можно определить, как измерения, средние квадратические ошибки которых различны. Для характеристики таких измерений берут величину, называемую вес измерения. Вес определяется по формуле: 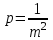 . То есть, чем больше вес измерения, тем более точным является результат. . То есть, чем больше вес измерения, тем более точным является результат.Доказано, что вес средней арифметической средины вычисляется по формуле: 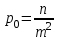 , то есть он в n раз больше веса измерения. , то есть он в n раз больше веса измерения.Определить наиболее точное значение, то есть общую среднюю арифметическую средину, можно через веса по формуле 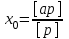 , где x0 – общая средняя арифметическая средина, a – результат измерения, а p – его вес. , где x0 – общая средняя арифметическая средина, a – результат измерения, а p – его вес.Примеры Даны измерения угла и их средние квадратические ошибки: 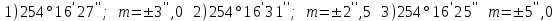 . Найти наиболее надежное значение угла. . Найти наиболее надежное значение угла.Решение:  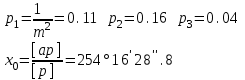 Даны результаты измерения углов и их средние квадратические ошибки. Найти наиболее точное значение угла. 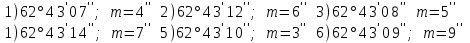 Решение: 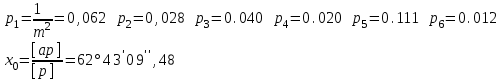 При решении задач, в которых измеряется один и тот же угол, но разными количествами приемов, за вес измерения берется количество приемов, для определения наиболее точного результата. Если же определяется наиболее точное значение высоты по различной длине хода, то за вес принимается величина, обратная длине хода. Даны измерения угла и количество приемов, которыми они были измерены: 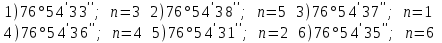 . Найти наиболее надежное значение угла. . Найти наиболее надежное значение угла.Решение. 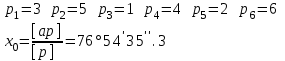 4) Дана отметка точки, полученная по шести ходам нивелирования. Определить наиболее надежное значение точки. 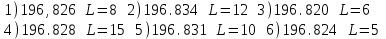 Решение: 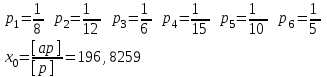 Двойные неравноточные измерения При определении оценки точности неравноточных измерений используют понятие средняя квадратическая ошибка единицы веса (или ошибка единицы веса). Обозначается эта ошибка µ. Пусть вес какого-либо измерения (возможно несуществующего) равен единице. Тогда через истинные ошибки измерения ошибку единицы веса можно найти по формуле: 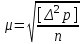 , где n – количество измерений, p – вес измерения, Δ – истинная ошибка измерения. , где n – количество измерений, p – вес измерения, Δ – истинная ошибка измерения. Также ошибку единицы веса можно вычисли через отклонения от средней арифметической средины по формуле: 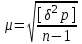 , где δ – отклонение от средней арифметической средины. , где δ – отклонение от средней арифметической средины.Через ошибку единицы веса можно также выразить среднюю квадратическую ошибку арифметической средины по формуле: 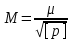 . .Двойные неравноточные измерения – неравноточные измерения, выполненные дважды. При оценке точности таких измерений, также как и при оценке точности двойных равноточных измерений, используют разности измерений. Разности двойных неравноточных измерений d: 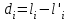 , если при первом измерении были получены результаты , если при первом измерении были получены результаты 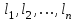 , а при вторых – , а при вторых – 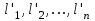 . .Если эти неравноточные измерения были попарно равноточны, то есть 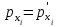 , то вес разности измерения будет , то вес разности измерения будет 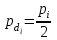 . Тогда средние квадратические ошибки средних значений . Тогда средние квадратические ошибки средних значений 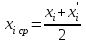 будут равны будут равны 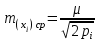 , где µ – ошибка единицы веса, p – вес измерения. , где µ – ошибка единицы веса, p – вес измерения.Пример Даны разности двойных неравноточных измерений и веса соответствующих измерений. Найти средние квадратические ошибки средних значений 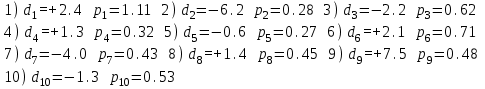 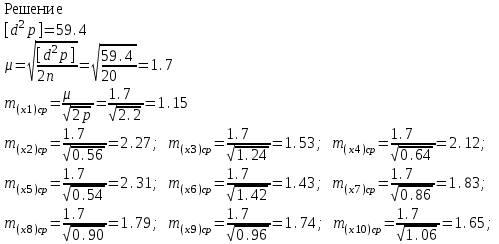 Таким образом, несмотря на то, что найти истинный результат измерения практически невозможно, можно найти наиболее близкий к нему. Определенная точность полученного результата влияет на возможность его применения в той или иной области строительства. Например, минимальная точность измерения углов может меняться от средней квадратической погрешности3’’ до средней крадратический погрешности 30’’ при строительстве разных типов зданий. При строительстве дорог, например, максимальная средняя квадратическая погрешность 30’’ и, поэтому, погрешность в 15’’будет допустимой. Для групп зданий не участках площадью меньше 1 км2, для которого средняя квадратическая погрешность будет 10’’, 15’’ уже не допустимая погрешность. Также изменяется и минимальная точность измерения превышений, от средней квадратической погрешности 4 мм, до 15мм. Для дорог – максимальная погрешность в 15 мм, а для предприятий и групп зданий на участках площадью более 1 кв км– 4мм, то есть от определения погрешности зависит можно ли учитывать результаты измерений при строительстве того или иного сооружения или же необходимо получить более точный результат. |
