статья_Пеленко. Влияние процесса обратного перетока материала на закономерности формирования давления по длине шнековой поверхности экструдеров
 Скачать 350.29 Kb. Скачать 350.29 Kb.
|
|
Научный журнал НИУ ИТМО. Серия «Процессы и аппараты пищевых производств» № 1, 2021 УДК 519.68:532.7:541.8:541.182.41 Влияние процесса обратного перетока материала на закономерности формирования давления по длине шнековой поверхности экструдеров д-р техн. наук В.В. Пеленко, pelenko1@rambler.ru канд. техн. наук А.А. Верхоланцев, verxolantsev@rambler.ru Санкт-Петербургский государственный университет промышленных технологий и дизайна 198095, Россия, Санкт-Петербург, ул. Ивана Черных, 4 канд. техн. наук А.П. Верболоз, spb.alek@yandex.ru канд. техн. наук В.А. Демченко, dem8484@gmail.com И.И. Усманов, ilhomusmanov@mail.ru, Ч. Ся, xcg19997118320@gmail.com Университет ИТМО 191002, Россия, Санкт-Петербург, ул. Ломоносова, 9 Поставлена и аналитически решена задача описания закона нарастания внутришнекового давления твердообразного материала по длине винтовой поверхности экструдера в зависимости не только от распределенных сил трения и сосредоточенных сил сопротивления ребер противовращения, выполненных на внутренней поверхности корпуса экструдера, но и с учетом процесса «шлюзования» – обратного перетока материала, существенно влияющего на формирование поля давлений. Полученная математическая модель позволяет более корректно обосновывать конструктивные и технологические параметры экструдеров и измельчителей. Сложность движения материала в шнековых агрегатах в процессе его транспортирования, экструзии и резания обусловлена не только сложной винтовой формой канала, но и влиянием большого числа переменных технологических параметров, конструктивных элементов механизма, а также многих факторов физико-механического и реодинамического характера. В частности, в данном исследовании структурированы и аналитически описаны методами дифференциального исчисления процессы в двух характерных зонах шнекового пространства, принципиально отличающихся по физическим условиям. Первая зона определяется отсутствием процесса «шлюзования» при нарастании внутришнекового давления от начального значения Ро до величины Рш, вызывающей начало обратного тока материала. Во второй зоне винтового шнека имеет место процесс «шлюзования» при нарастании давления от величины начала обратного тока Рш до давления Рэ экструзии материала через отверстия выходной измельчительной решетки. В этой второй зоне существенно изменяется характер течения продукта и запись дифференциального уравнения перемещения материала. Исходя из полученной математической модели для закона распределения давления по длине шнековой поверхности могут быть оптимизированы конструктивные и технологические характеристики экструдеров для снижения энергоемкости процессов измельчения материалов. Ключевые слова: математическое описание; дифференциальное уравнение; закон изменения давления; экструзия; обратный переток; шнековая поверхность. DOI: 10.17586/2310-1164-2021-14-1-15-24 Influence of the material reverse flow process on the regularities of pressure formation along the length of the screw surface of extruders D. Sc. Valery V. Pelenko, pelenko1@rambler.ru Ph. D. Alexander A. Verkholantsev, verxolantsev@rambler.ru St. Petersburg State University of Industrial Technology and Design 4, Ivan Chernykh str., St. Petersburg, 198095, Russia Ph. D. Vera A. Demchenko, dem8484@gmail.com Ilhom I. Usmanov, ilhomusmanov@mail.ru Chenguang Xia, xcg19997118320@gmail.com ITMO University 9, Lomonosov str., St. Petersburg, 191002, Russia In the present work, the problem of describing the law of increase in the internal screw pressure of a solid material along the length of the screw surface of the extruder is posed and analytically solved, depending not only on the distributed friction forces and concentrated resistance forces of the counter-rotation ribs, made on the inner surface of the extruder body, but also taking into account the process of "sluicing" – backflow of material, which significantly affects the formation of the pressure field. The obtained mathematical model makes it possible to more correctly substantiate the design and technological parameters of extruders and grinders. The complexity of the movement of material in screw aggregates during its transportation, extrusion and cutting is caused not only by the complex screw shape of the channel, but also by the influence of a large number of variable technological parameters, structural elements of the mechanism, as well as many factors of a physical, mechanical and rheodynamic nature. In particular, in this study, the processes in two characteristic zones of the screw space, which are fundamentally different in physical conditions, are structured and analytically described by differential calculus methods. The first zone is determined by the absence of the "slugging" process with an increase in the internal screw pressure from the initial value of Po to the value of Psh, which causes the beginning of the reverse flow of the material. In the second zone of the screw auger, the process of "sluicing" takes place with an increase in pressure from the value of the onset of the reverse current Psh to the pressure Pe of extrusion of the material through the openings of the outlet grinder. In this second zone, the nature of the product flow and the record of the differential equation of material movement change significantly. Based on the obtained mathematical model for the law of pressure distribution along the length of the screw surface, the design and technological characteristics of extruders can be optimized to reduce the energy consumption of materials grinding processes. Keywords: mathematical description; differential equation; pressure change law; extrusion; reverse flow; screw surface. Введение Как известно, одним из главных параметров, определяющих качество процесса измельчения материалов, а также энергоемкость процесса экструзии и перемещения в шнековом канале волчка, является величина давления, формируемого на выходе в зоне резания. Требуемая величина этого давления аналитически определена в классической работе А.И. Пелеева [1] и уточнена в исследовании [2]. При этом в работе [3] решена задача оптимизации момента затяжки зажимной гайки волчка, исключающего проникновение материала в стык конструктивной пары нож–решетка и обеспечивающего качество резания и измельчения. Аналитическое решение задачи определения закона нарастания давления по длине шнекового канала при различных степенях и уровнях упрощений осуществлено в работах [3, 4] и ряде других. Тем не менее, в указанных исследованиях формирование определяющего давления на выходе из экструдера описывается лишь в зависимости от тормозящего действия на материал сил трения о винтовую поверхность шнека [5]. Как известно, для таких шнековых механизмов, как волчки и мясорубки, основным фактором, определяющим закон нарастания давления, является наличие элементов противовращения на внутренней поверхности цилиндрического корпуса в виде буртиков или шлицов. В связи с этим в работе [6] решена задача математического описания процесса формирования внутришнекового давления с учетом воздействия на экструдируемый материал сил механического сопротивления элементов противовращения. В исследовании [7] авторами работы получено решение, осложненное рассмотрением конической формы корпуса экструдера. Однако до настоящего времени отсутствует теоретическое описание влияния процесса «шлюзования» – возникновения обратного перетока материала через винтовой просвет между внутренней винтовой поверхностью буртика противовращения в корпусе экструдера и наружной винтовой поверхностью витков шнека на формирование закона распределения внутришнекового давления. Цель работы – математическое описание закона изменения внутришнекового давления с учетом явления «шлюзования» во второй фазе процесса экструзии. Объекты и методы исследования Объектами исследования являются процессы взаимодействия сырья с конструктивными элементами шнековых экструдеров, волчков или мясорубок при перемещении, деформации и экструзии твердообразного материала в условиях противодавления со стороны буртиков противовращения, выполненных на внутренней поверхности корпуса, а также с учетом явления «шлюзования» в зоне возникновения обратного тока продукта. В качестве методов исследования выбрано математическое моделирование процесса формирования внутришнекового давления материала на основе построенной двухзонной физической модели и решение для каждой зоны определяющих дифференциальных уравнений. Результаты и обсуждение 1. Построение физической модели процесса экструзии Для математического описания процесса формирования внутришнекового давления рассматривали физическую модель перемещения пробки продукта в обращенном движении по поверхности винтового канала в двух его характерных зонах, учитывая влияние таких факторов тормозящего действия на внешнем контуре первой зоны, как сила трения, механическое сопротивление элементов противовращения, а во второй зоне шнекового пространства также дополнительное появление обратного тока продукта. Структуризация двухзонного шнекового пространства и конструктивные параметры элементов экструдера приведены на рисунке 1. 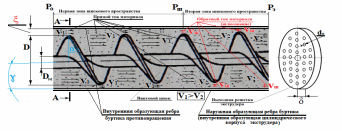 Рисунок 1 – Структуризация зон шнекового пространства экструдера Figure 1. 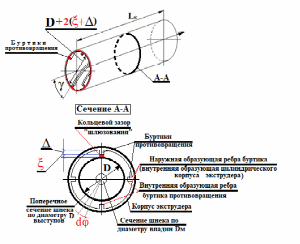 Рисунок 2 – Схема и параметры кольцевого зазора в поперечном сечении А-А экструдера Figure 2. В первой зоне шнекового пространства экструдера (измельчителя, волчка, мясорубки) сохраняется однонаправленное поступательное перемещение материала (скорость V1) до определенного значения роста давления (от Ро до Рш). Однако, при достижении критического давления Рш (давление начала «шлюзования» – обратного перетока продукта), действующие на материал сжимающие силы становятся достаточными, чтобы осуществить срез продукта и его обратное перемещение (скорость Vш) сквозь винтовой щелевой зазор, просвет ξ, между внутренней винтовой поверхностью ребер противовращения корпуса экструдера и наружной винтовой поверхностью витков шнека, как это показано на рисунках 1 и 2. Начиная с этого значения Рш, в связи с перераспределением скоростей V1 и V2, а также характера действующих сил, давление во второй зоне изменяется по иному закону, чем в первой зоне, увеличиваясь до требуемого давления Рэ экструзии материала сквозь отверстия выходной решетки. Разработанная физическая модель и проведенное ее содержательное описание позволяют перейти к изложению математических особенностей формирования поля давлений в каждой из выделенных зон. 2. Построение общей математической модели процесса экструзии За основу общей математической модели процесса принимаем гидродинамические уравнения движения в форме Эйлера для массы продукта единичного объема [8], преобразованные в уравнения равновесия сил, действующих на элементарную пластину внутришнекового пространства. В качестве элементарной пластины будем рассматривать призму, образованную двумя нормальными к винтовой линии шнека секущими плоскостями с расстоянием между ними dX, как это изображено на рисунке 3. 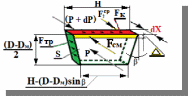 Рисунок 3 – Расчетная схема действия сил на элементарную пластину Figure 3. Запишем уравнение перемещения призматической пластины экструдируемого материала в обращенном движении в форме уравнения Эйлера, проектируя его на продольную ось Х развернутого винтового канала под действием силы искомого давления Р и сил трения и сопротивления R, противодействующих этому перемещению и приложенных к массе единичного объема 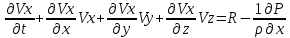 , (1) , (1)где 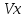 – проекция вектора скорости перемещения материала на ось ОХ, м/с; – проекция вектора скорости перемещения материала на ось ОХ, м/с;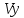 , , 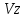 – соответствующие проекции вектора скорости на оси ОYи OZ, м/с; – соответствующие проекции вектора скорости на оси ОYи OZ, м/с;t – время, с; ρ – плотность экструдируемого материала, кг/м3; P – давление материала на выходе из шнекового механизма, Па; R – проекция на ось OX главного вектора внешних сил трения, а также сопротивления, действующих на массу единичного объема призмы, Н/кг или м/с2; Нас интересует установившийся режим течения экструдируемого сырья по винтовому каналу шнека, поэтому, пренебрегая наличием поперечного перемещения пищевого материала вдоль осей OY и OZ можем положить 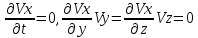 . (2) . (2)Принимая во внимание условие неразрывности потока массы, полагаем, что инерционная составляющая также равна нулю 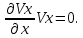 (3) (3)Таким образом, базовое для двузонной задачи с учетом допущений (2) и (3), уравнение (1) равновесия Эйлера для массы единичного объема материала в общем виде примет вид 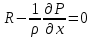 . .Для массы призмы величиной 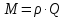 , получим , получим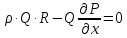 , (4) , (4)где 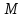 – масса призмы пищевого материала, кг; – масса призмы пищевого материала, кг;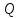 – объем призмы перемещаемого материала под действием градиента давления, м3; – объем призмы перемещаемого материала под действием градиента давления, м3;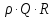 – проекция на ось ОХ главного вектора всех внешних сил, действующих на весь объем призмы, Н. – проекция на ось ОХ главного вектора всех внешних сил, действующих на весь объем призмы, Н.Полученное обобщенное уравнение равновесия (4) следует раскрыть в виде конкретных компонентных уравнений для различных по характеру действующих сил, первой и второй зоны шнекового пространства. 2.1. Построение математической модели процесса экструзии в первой зоне шнекового пространства Как следует из расчетной схемы, представленной на рисунке 3, в пределах первой зоны шнекового пространства уравнение равновесия не содержит составляющей F2ср, так как давление пока недостаточно для среза и обратного тока – «шлюзования» материала, поэтому можем записать 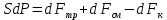 . (5) . (5)Раскроем содержание слагаемых компонентов уравнения (5), формирующих давление P на элементарной пластине материала площадью S и толщиной dX(рисунок 3). Дифференциал силы трения dFтр материала о винтовую поверхность, формирующий поле давления в шнековом канале, определяется по очевидному соотношению 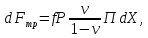 (6) (6)где P – давление материала в шнековом канале, Па; П – периметр трения материала о винтовую поверхность, м. В соответствии с физической моделью процесса экструзии и расчетной схемой, приведенной на рисунке 3, величина периметра трения материала о винтовую поверхность определяется очевидным соотношением 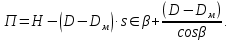 Площадь давления S на элементарную пластину определяется в соответствии с рисунком 3 по выражению 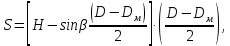 где D– величина диаметра образующего цилиндра выступов шнековой винтовой поверхности, м; Dм – диаметр впадин шнековой винтовой поверхности, м; β – половина угла заострения винта шнека (рисунок 3), рад. Как показано в работе [9], дифференциал силы противодействия со стороны буртиков противовращения определяется их количеством, высотой Δ, геометрическими характеристиками элементарной пластины и ее угловой координацией 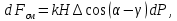 (7) (7)где k – количество буртиков противовращения; H– ширина шнекового канала по выступам винтовой поверхности (рисунок 3), м; 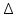 – высота буртиков противовращения, м; – высота буртиков противовращения, м;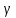 – угол наклона образующей буртика к продольной оси шнека (рисунок 1), рад. – угол наклона образующей буртика к продольной оси шнека (рисунок 1), рад.При этом ширина шнекового канала по выступам винтовой поверхности определяется соотношением 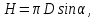 где 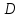 – диаметр шнека по выступам винтовой поверхности (рисунок 3), м. – диаметр шнека по выступам винтовой поверхности (рисунок 3), м.Дифференциал силы трения dFк материала о внутреннюю поверхность цилиндрического корпуса экструдера определяется в соответствии с рисунками 1 и 3  (8) (8)Подставляя полученные соотношения (6) – (8) в уравнение (5), получим  (9) (9)Решение дифференциального уравнения (9) для граничного условия  , при , при  , получено в виде , получено в виде Таким образом, закон нарастания давления в первой зоне шнекового пространства  , приобретает вид , приобретает вид (10) (10)Выразим условие начала процесса обратного тока продукта через соотношение равновесных напряжений смятия материала о буртик противовращения и удельного усилия резания, вызывающего процесс шлюзования (рисунок 2), в виде  . .Тогда получим граничное условие для давления «шлюзования»  (11) (11)Решая совместно систему уравнений (10) и (11) относительно Х, получаем длину винтовой линии шнека, после достижения которой обеспечивается искомое давление шлюзования материала на выходе из первой зоны экструдера  . (12) . (12)Определив координату начала процесса «шлюзования»  , можем перейти к разработке математической модели процесса экструзии материала во второй зоне. , можем перейти к разработке математической модели процесса экструзии материала во второй зоне.2.2. Построение математической модели процессаэкструзии во второй зоне шнекового пространства Как следует из расчетной схемы, представленной на рисунке 3, в пределах второй зоны шнекового пространства, в уравнение равновесия добавляется составляющая  , так как давление материала превышает давление, достаточное для среза и обратного тока – «шлюзования», поэтому можем записать , так как давление материала превышает давление, достаточное для среза и обратного тока – «шлюзования», поэтому можем записать . (13) . (13)Раскроем содержательную часть последнего слагаемого, характеризующего возникновение процесса «шлюзования» начиная с координаты  . .Дифференциал силы  , вызывающей обратный переток материала (эффект «шлюзования») определяется в соответствии с рисунком 1 аналогично соотношению (7), но с учетом понижения текущего значения давления на величину , вызывающей обратный переток материала (эффект «шлюзования») определяется в соответствии с рисунком 1 аналогично соотношению (7), но с учетом понижения текущего значения давления на величину  . . Таким образом, можем записать  (14) (14)где ξ – величина зазора между внешним образующим цилиндром поверхности выступов шнека и внутренним образующим цилиндром поверхности выступов буртиков противовращения, как это указано на рисунках 1 и 2, м. Подставляя полученное соотношение (14) в уравнение (13) и учитывая равенство дифференциалов dР и  получим получим (15) (15)Решение этого дифференциального уравнения (15) для второй зоны получено методом разделения переменных для граничных условий, в соответствии с уравнениями (11) и (12), при  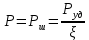 в виде в виде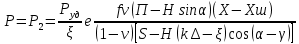 . (16) . (16)Учитывая соотношение (12) для координаты начала процесса «шлюзования», полученное уравнение (16) процесса формирования давления во второй зоне после ряда алгебраических преобразований примет вид экспоненциального закона 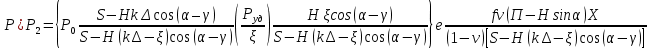 . (17) . (17)Корректность полученного закона для второй зоны шнекового пространства подтверждается равенством уравнений (10) и (17) при 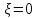 , то есть при отсутствии явления шлюзования. , то есть при отсутствии явления шлюзования.2.3. Определение критерия оптимальности процесса экструзии, исключающего явление обратного перетока материала («шлюзования») и обеспечивающего минимизацию энергозатрат Как отмечалось ранее, в работе [2] осуществлено теоретическое обоснование величины требуемого давления экструзии в плоскости измельчительной решетки с учетом сил трения в условиях стесненного сжатия пищевого материала 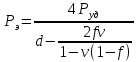 . (18) . (18)Из уравнения (18) следует [2, 10, 11], что величина требуемого давления экструзии 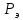 в зоне решетки определяется не только таким геометрическим параметром отверстия, как его диаметр, а также удельным усилием резания в зоне решетки определяется не только таким геометрическим параметром отверстия, как его диаметр, а также удельным усилием резания 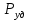 , характеризующим прочностные свойства сырья, но и коэффициентом Пуассона ν, определяющим деформационные свойства материала, коэффициентом трения сырья f, свидетельствующем о характере трибологического взаимодействия пищевого материала с цилиндрической поверхностью отверстия измельчительной решетки толщиной d. , характеризующим прочностные свойства сырья, но и коэффициентом Пуассона ν, определяющим деформационные свойства материала, коэффициентом трения сырья f, свидетельствующем о характере трибологического взаимодействия пищевого материала с цилиндрической поверхностью отверстия измельчительной решетки толщиной d. После получения нами граничного условия для давления «шлюзования» в форме соотношения (11), становится совершенно ясно, что критерием исключения в процессе перемещения пищевого сырья обратного перетока продукта через кольцевой зазор между наружной винтовой поверхностью шнека и внутренней образующей поверхностью буртика противовращения, будет очевидное неравенство 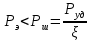 . .В таком случае, как следует из работ [12, 13], после решения системы уравнений (11) и (18) критерием отсутствия «шлюзования» становится следующее соотношение, связывающее конструктивные параметры выходной измельчительной решетки (d, δ) и шнекового механизма (ξ)  . (19) . (19)2.4. Графическое построение поля давлений вдоль винтовой поверхности шнека Для построения конкретных зависимостей (10) и (17) в первой и второй зонах внутришнекового пространства примем следующие реальные исходные и расчетные (П и S) данные. Dи = 0,06 м; Dм = 0,02 м; d = 0,003 м; δ = 0,005 м; Н = 0,133 м; β = 0,2 рад.; f= 0,10; ν = 0,43; α = π/4; γ = 0; Δ = 0,002 м; ξ = 0,001 м; k = 4; S = 0,0021 м2; П = 0,162 м; Ро = 105 Па; Руд = 400 Н/м. Координата начала процесса «шлюзования» определяется по соотношению (12) и для принятых исходных данных составит величину Хш = 0,2628·1,3863 = 0,364 м. В таком случае уравнения (10), (11) и (16) примут вид  ; (20) ; (20) ; (21) ; (21) (22) (22)При этом требуемое давление экструзии через отверстия выходной решетки вычисляется по соотношению (18). 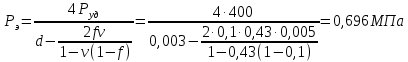 . . Подставляя полученное значение в уравнение (22), и учитывая соотношение (21), определим требуемую длину Хт винтовой поверхности, обеспечивающую эту величину: Хт = 0,519 м. Как видим, на длине от Хш = 0,364 м до Хт = 0,519 м происходит процесс «шлюзования». Для исключения явления «шлюзования» требуется выполнение условия (19): 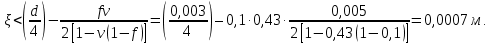 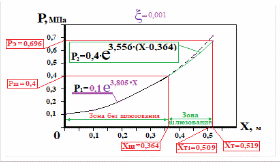 Построение графиков полученных функций Р1(Х) и Р2(Х) выполнено на рисунке 4. Рисунок 4 – Функциональная зависимость давлений в «безшлюзовой» зоне и в зоне «шлюзования» от длины шнековой поверхности Figure 3. Для исключения явления «шлюзования» требуется выполнение условия (19) 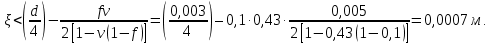 В этом случае требуемая длина шнековой поверхности вычисляется по уравнению (20) и составит величину Хт1 = 0,509 м, что дает возможность конструкторам уменьшить габариты и массу шнекового измельчителя на 2% и более. При существующем парке измельчительно-режущего оборудования различной производительности в десятки и сотни тысяч единиц, величина экономии представляется весьма существенной. Выводы В работе показано, что при превышении некоторого давления Рэ в шнековом пространстве волчков и измельчителей возникает обратный ток продукта – явление «шлюзования», приводящее к повышенному расходу энергии и снижению качества сырья из-за его дополнительного мятия. Рассмотрены две характерные зоны (первая – «безшлюзовая» и вторая – «шлюзовая»), для которых получены отличающиеся аналитические зависимости давления материала P от длины шнековой поверхности Х. Определен критерий начала процесса «шлюзования» – соотношение давления экструзии и удельного усилия резания материала. Полученный критерий выражен через взаимосвязанные конструктивные параметры выходной измельчительной решетки (d, δ) и шнекового механизма (ξ). При известном давлении экструзии определена координата Хш начала процесса обратного перетока материала. Показано, что исключив процесс «шлюзования» за счет совершенствования конструкции уменьшением зазора ξ, имеется возможность сократить размеры и материалоемкость волчков и мясорубок на 2% и более, что составляет при существующем парке оборудования в сотни тысяч единиц, существенную величину. Литература Пелеев А.И., Козорез С.А. Современные конструкции волчков. М., 1970. 47 с. Пеленко В.В., Малявко Д.П., Усманов И.И., Екимов В.Г., Крысин А.Г. Оптимизация процесса измельчения пищевых материалов в волчках // Научный журнал НИУ ИТМО. Серия: Процессы и аппараты пищевых производств. 2016. № 2. С. 32–39. Силин В.А. Исследование и расчет основных параметров щнековых машин для переработки пластичных масс: автореф. дис. … д-ра техн. наук. Калинин, 1969. 48 с. Сидоряк А.Н., Бесидский А.В., Юрков С.Г., Якушев О.И. Разработка математической модели волчка // Мясная индустрия, 2003. № 1. С. 37–40. Мачихин Ю.А., Берман Г.К., Клаповский Ю.В. Формование пищевых масс. М.: Колос, 1992. 272с. Пеленко В.В., Иваненко В.П., Шахов А.С., Усманов И.И., Денисов А.А., Халиков И.И. Аналитическое и экспериментальное моделирование профиля давления сырья в волчках // Научный журнал НИУ ИТМО. Серия: Процессы и аппараты пищевых производств. 2019. № 2. С. 80–89. Лепеш Г.В., Пеленко В.В., Хлыновский А.М., Усманов И.И. Оценка влияния конусности корпуса экструдера на закон распределения давления по его длине // Технико-технологические проблемы сервиса. 2020. № 2. С. 48–54. Кочин Н.Е., Кибель И.А., Розе Н.В. Теоретическая гидромеханика. Ч.1 М.: Физматлит, 1963. 583 с. Пеленко В.В., Хлыновский А.М., Усманов И.И., Ся Ч. Влияние элементов противовращения на закон изменения внутришнекового давления экструдеров Научный журнал НИУ ИТМО. Серия: Процессы и аппараты пищевых производств. 2020. № 3. С. 46–53. Агеев О.В., Наумов В.А., Фатыхов Ю.А., Самойлова Н.В. Математическое моделирование сил нормального контактного давления на наклонные грани ножа при резании рыбы // Известия КГТУ. 2017. № 47. C. 80–96. Усманов И.И., Пеленко В.В. Элементы теории расчета волчков. СПб.: Ношир, 2018. 88 с. Фатыхов Ю.А., Агеев О.В. Математическая модель процесса резания рыбного филе дисковым ножом // Известия КГТУ. 2007. № 12. C. 42–51. Остриков А.Н., Абрамов О.В., Рудометкин А.С. Экструзия в пищевой промышленности. СПб.: ГИОРД, 2004. 288 с. References Peleev A.I., Kozorez S.A. Modern designs of tops. Moscow, 1970. 47 p. (In Russian). Pelenko V.V., Malayvko D.P., Usmanov I.I., Ekimov V.G., Krysin A.G.Optimization of food grinding process in grinders. Processes and Food Production Equipment. 2016, no. 2n pp. 32–39. (In Russian). Silin V.A. Research and calculation of the main parameters of screw machines for processing plastic masses. Extended abstract of Doctor’s thesis. Kalinin, 1969. (In Russian). Sidoryak A.N., Besidsky A.V., Yurkov S.G., Yakushev O.I. Development of a mathematical model of the top. Meat Industry, 2003, no. 1, pp. 37–40. (In Russian). Machikhin Yu.A., Berman G.K., Klapovsky Yu.V. Molding food masses. Moscow, Kolos Publ., 1992. 272 p. (In Russian). Pelenko V.V., Ivanenko V.P., Shakhov A.S., Usmanov I.I., Denisov A.A., Khalikov I.I.Analytical and experimental modeling of the raw material pressure profile in tops. Processes and Food Production Equipment. 2019, no. 2, pp. 80–89. (In Russian). Lepesh G.V., Pelenko V.V., Khlynovsky A.M., Usmanov I.I. Assessment of the influence of the taper of the extruder body on the law of pressure distribution along its length. Technico-tehnologicheskie problemy servisa. 2020, no. 2, pp. 48–54. (In Russian). Kochin N.E., Kibel I.A., Rose N.V. Theoretical hydromechanics. Part 1. Moscow, Fizmatlit Publ., 1963. 583 p. (In Russian). Pelenko V.V., Khlynovsky A.M., Usmanov I.I., Xia Ch.Influence of counter-rotation elements on the law of pressure change inside the extruder screw. Processes and Food Production Equipment. 2020, no. 3, pp. 46-53. (In Russian). Ageev O.V., Naumov V.A., Fatykhov Yu.A., Samoilova N.V. Mathematical simulation of forces of normal contact pressure of inclined knife edges during fish processing. Izvestia KSTU. 2017, no. 47, pp. 80–96. (In Russian). Usmanov I.I., Pelenko V.V. Elements of the theory of calculating tops. St. Petersburg, Noshir Publ., 2018. 88 p. (In Russian). Fatykhov Yu.A., Ageev O.V. Mathematical model of the process of cutting fish fillets with a disk knife. Izvestia KSTU. 2007, no. 12, pp. 42–51. (In Russian). Ostrikov A. N., Abramov O. V., Rudometkin A. S. Extrusion in the food industry. St. Petersburg: GIORD, 2004. 288 p. (In Russian). Статья поступила в редакцию 09.12.2020  |
