Правила и инструкции. своя игра. ПРАВИЛА и инструкции. СВОЯ ИГРА. Скоро ЕГЭ. Внеурочное мероприятие "Своя игра" (Скоро егэ) Автор разработки
 Скачать 3.71 Mb. Скачать 3.71 Mb.
|
|
Внеурочное мероприятие "Своя игра" («Скоро ЕГЭ») Автор разработки: Белякова Ольга Владимировна, учитель математики МОУ «ЛСОШ №2» г.Лихославль Тверской области. Целевая аудитория: учащиеся 11-х классов. Цели:- обучающие: повторение, систематизация и закрепление знаний, приобретаемых на уроках математики; расширение кругозора и математической культуры учащихся; подготовка к ЕГЭ; - развивающие: развивать умение анализировать, сравнивать; развивать внимание, логическое мышление; развивать умение организовывать учебное сотрудничество с учителем и сверстниками (участниками своей команды и командами соперников); - воспитательные: развивать познавательный интерес к математике и регулятивные навыки через игровые моменты; развивать коммуникативные способности во время работы в группах; способствовать пониманию необходимости интеллектуальных усилий для успешного обучения и подготовке к ЕГЭ. Мероприятие построено по принципу одноименной телевизионной игры. Все вопросы, использованные в викторине, заимствованы из тематических сборников для подготовки к ЕГЭ (2015-2016 гг.) Участники игры: три команды по 5 человек (учащиеся 11-х классов).  Ведущий игры (учитель) управляет интерактивной презентацией. Помощник ведущего ведет подсчет баллов, заработанных командами, на доске. Команда, находящаяся за центральным столом, начинает игру - выбирает один из вопросов: тему и стоимость. Игра состоит из двух раундов по 30 вопросов в раунде и финального раунда из 1 вопроса. Вопросы первого и второго раундов сгруппированы в 6 тем по 5 вопросов. Стоимость вопросов: 10, 20, 30, 40, 50 баллов - в каждом раунде. Решение обсуждается командами, ответ на вопрос (если необходимо, стоимость вопроса) дает (пишет) капитан команды. Право ответа на вопрос получает та команда, игрок которой первым поднял руку (сигнал о готовности команды дать ответ). Если был дан неверный ответ на вопрос, то остальные команды могут использовать свое право ответа, дав сигнал о готовности отвечать (поднятая рука).  Темы первого раунда: Рациональные уравнения; Текстовые задачи; Иррациональные выражения; Степенные выражения; Тригонометрические выражения; Логарифмические выражения.  Темы второго раунда: Практико-ориентированные задачи; Практико-ориентированные задачи(2); Вероятность; Планиметрия; Площадь; Стереометрия. Команды имеют право, но не обязаны отвечать на заданный вопрос. Правильный ответ приносит команде сумму, равную стоимости вопроса на игровом табло. Неправильный ответ лишает команду указанной суммы (баллы снимаются со счета команды). Команда, правильно ответившая на вопрос, получает право выбрать следующий вопрос (тему и стоимость). В первых двух раундах вместо любого вопроса командам могут выпасть "кот в мешке" или "аукцион". Количество "котов в мешке" и "аукционов" в каждом раунде и их расположение не регламентируется. Если выпал "Кот в мешке", то команда, выбравшая "кота", обязана отдать его любому из своих соперников. После этого на табло высвечивается тема вопроса, его стоимость и сам вопрос. Отвечает только та команда, кому был отдан этот вопрос. "Аукцион" - вопрос разыгрывается с командой, назначившей за него наибольшую цену на торгах. Остальные команды на этот вопрос не отвечают. Очерёдность подачи заявок определяется ведущим игры. Ставка "ва-банк" перебивается только большим по сумме "ва-банком". Если сумма на счету игрока меньше начальной стоимости вопроса, следует автоматическая ставка, равная номиналу вопроса. Ставки на "аукционе" кратны 10 баллам. Отсутствие ответа на "кота в мешке" и на "аукцион" приравнивается к неправильному ответу (и заявленные баллы снимаются со счета команды). Переход ко второму раунду осуществляется после того, как сыграют все вопросы первого раунда. Переход к финальному раунду осуществляется после того, как сыграют все вопросы второго раунда. В финальном раунде из пяти предложенных тем команды выбирают одну. Командам по очереди предлагается убрать одну из предложенных на табло тем, пока на табло не останется всего одна тема. Она и будет разыгрываться (указанные командами темы исчезают с экрана после нажатия на кнопки с их названиями).  Темы финального раунда: Вклады; Вероятность; Стереометрия; Наибольшее и наименьшее значения функции; Исследование функций. Стоимость вопроса финального раунда определяет для себя каждая команда, исходя из набранной в предыдущих раундах суммы. Минимальная ставка - 1 балл, максимальная - "ва-банк". Свое количество баллов и ответ на финальный вопрос каждая команда пишет на листе бумаги. На обдумывание (решение) дается 5 минут. Затем каждая команда по очереди показывает то, что она написала на листе бумаги, и озвучивает свое количество баллов и свой ответ на вопрос. Если ответ верный, то команда зарабатывает это количество баллов. Если ответ неверный, то у команды снимается это количество баллов. Победителем игры становится команда, набравшая наибольшую сумму баллов после финального раунда. Подведение итогов. Ведущий, подсчитывает баллы, определяет команду-победителя и вручает ей диплом. Управление презентацией. Управление презентацией реализуется с помощью кнопок, гиперссылок и триггеров.   В II раунд ыбор вопроса на слайдах с меню осуществляется нажатием на соответствующую кнопку с суммой баллов. Переход ко второму раунду – нажатие на кнопку . III раунд Переход к третьему раунду – нажатие на кнопку . Выход При необходимости выйти из программы – кнопка . Появление правильного ответа на слайдах с вопросами – нажатие левой кнопкой мыши на любом свободном месте экрана (подсказка – на экране).   Д Назад ля возврата на слайд меню – нажать на кнопку . На слайдах меню кнопки с указанием баллов, уже сыгравших вопросов, исчезают и больше не высвечиваются (таким образом, их повторный выбор невозможен).  Выбор темы игры в финальном раунде осуществляется следующим образом: команды по очереди называют тему, которую следует убрать; ведущий нажимает на кнопку с названием выбранной темы; указанная тема исчезает с экрана. Таким образом, убираются четыре темы, и остается только одна тема в игре.   Играть Для перехода к вопросу по выбранной теме – нажать на кнопку Для выхода из игры – нажать кнопку «Выход». После этого осуществится переход на слайд с подведением итогов игры. 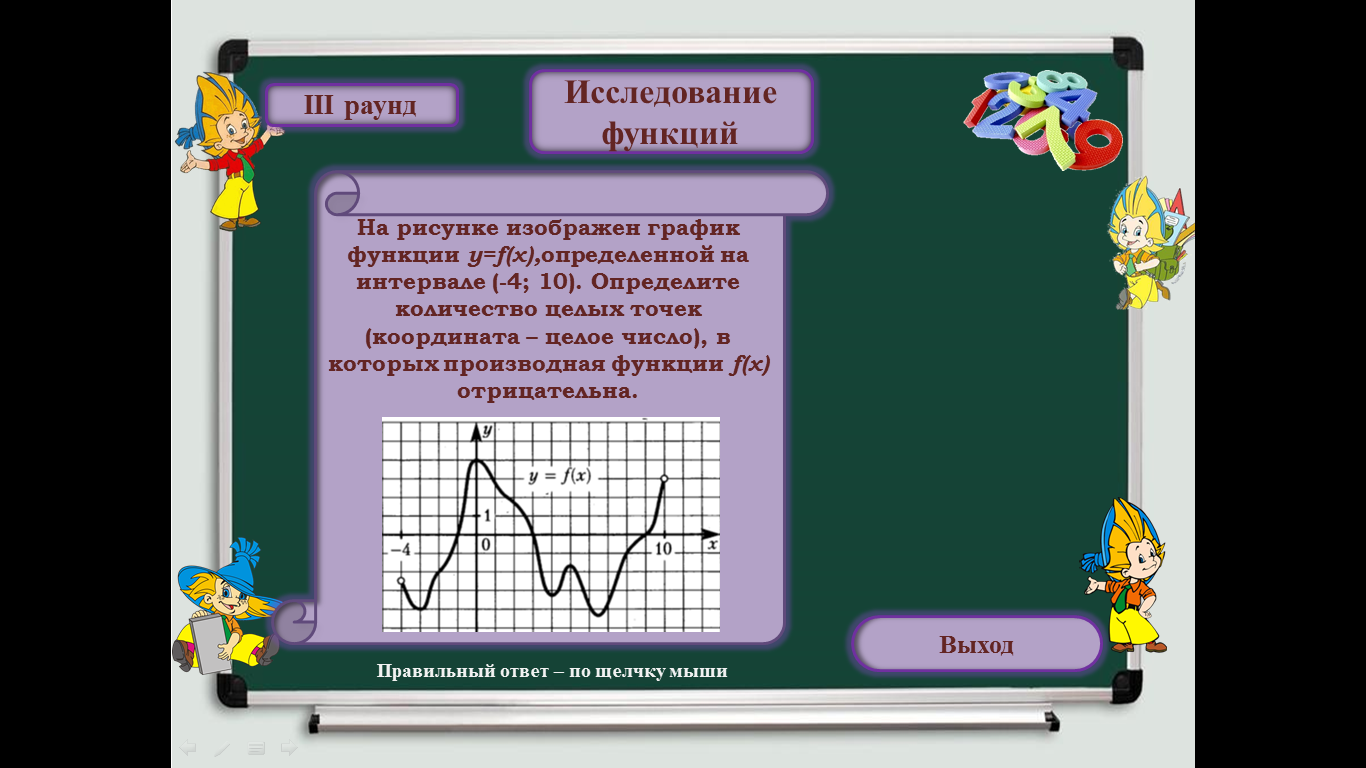  Вопросы и ответы викторины. 1 раунд Тема: Рациональные уравнения. Найдите корень уравнения 2 - 5х = 11 - 2х. Ответ: -3. Найдите корень уравнения 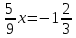 Ответ: - 3. Ответ: - 3.Найдите корень уравнения 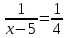 Ответ: 9. Ответ: 9.Найдите корень уравнения 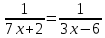 Ответ: - 2. Ответ: - 2.Найдите корень уравнения 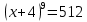 Ответ: - 2. Ответ: - 2.Тема: Текстовые задачи. Моторная лодка прошла против течения реки 117 км и вернулась в пункт отправления, затратив на обратный путь на 4 часа меньше. Найдите скорость лодки в неподвижной воде, если скорость течения равна 2 км/ч. Ответ дайте в км/ч. Ответ: 11. Первая труба пропускает на 5 литров воды в минуту меньше, чем вторая. Сколько литров воды в минуту пропускает первая труба, если резервуар объемом 150 литров она заполняет на 5 минут дольше, чем вторая труба? Ответ: 10. На изготовление 27 деталей первый рабочий тратит на 6 часов меньше, чем второй рабочий на изготовление 54 таких же деталей. Известно, что первый рабочий за час делает на 3 детали больше, чем второй. Сколько деталей в час делает второй рабочий? Ответ: 6. Смешали некоторое количество 18-процентного раствора некоторого вещества с таким же количеством 16-процентного раствора этого вещества. Сколько процентов составляет концентрация получившегося раствора? Ответ: 17. Путешественник переплыл море на яхте со средней скоростью 21 км/ч. Обратно он летел на спортивном самолете со скоростью 420 км/ч. Найдите среднюю скорость путешественника на протяжении всего пути. Ответ дайте в км/ч. Ответ: 40. Тема: Иррациональные выражения. Найдите значение выражения 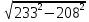 Ответ: 105. Ответ: 105.Найдите значение выражения 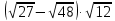 Ответ: - 6. Ответ: - 6.Найдите значение выражения 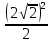 Ответ: 4. Ответ: 4.Найдите корень уравнения 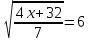 Ответ: 55. Ответ: 55.Найдите значение выражения 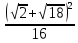 Ответ: 2. Ответ: 2.Тема: Степенные выражения. Найдите значение выражения 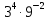 Ответ: 1. Ответ: 1.Найдите значение выражения 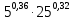 Ответ: 5. Ответ: 5.Найдите значение выражения 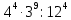 Ответ: 243. Ответ: 243.Найдите значение выражения 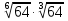 Ответ: 8. Ответ: 8.Найдите значение выражения 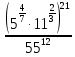 Ответ: 121. Ответ: 121.Тема: Тригонометрические выражения. Найдите 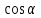 , если , если 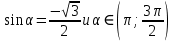 Ответ: - 0,5. Ответ: - 0,5.Найдите 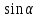 , если , если 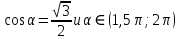 Ответ: - 0,5. Ответ: - 0,5.Найдите tg 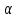 , если , если 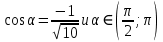 Ответ: - 3 . Ответ: - 3 .Найдите значение выражения 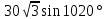 Ответ: - 45. Ответ: - 45.Найдите 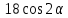 , если , если 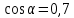 Ответ: - 0,36. Ответ: - 0,36.Тема: Логарифмические выражения. Найдите значение выражения 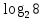 Ответ: 3. Ответ: 3.Найдите значение выражения 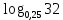 Ответ: - 2,5. Ответ: - 2,5.Найдите значение выражения 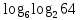 Ответ: 1. Ответ: 1.Найдите значения выражения 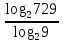 Ответ: 3. Ответ: 3.Вычислите значение выражения 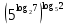 Ответ: 7. Ответ: 7.2 раунд Тема: Практико-ориентированные задачи. Летом килограмм клубники стоит 80 рублей. Маша купила 3 кг 500 г клубники. Сколько рублей сдачи она должна получить с 300 рублей? Ответ: 20. Для ремонта квартиры требуется 55 рулонов обоев. Сколько пачек обойного клея нужно купить, если одна пачка клея рассчитана на 4 рулона? Ответ: 14. Теплоход рассчитан на 900 пассажиров и 25 членов команды. Каждая спасательная шлюпка может вместить 60 человек. Какое наименьшее число шлюпок должно быть на теплоходе, чтобы в случае необходимости в них можно было разместить всех пассажиров и всех членов команды? Ответ: 16. В пачке 250 листов бумаги формата А4. За неделю в офисе расходуется 1 100 листов. Какое наименьшее количество пачек бумаги нужно купить в офис на 4 недели? Ответ: 18. По тарифному плану «Просто как день» компания сотовой связи каждый вечер снимает со счета абонента 22 рубля. Если на счету осталось меньше 22 рублей, то на следующее утро номер блокируют до пополнения счета. Сегодня утром у Лизы на счету было 400 рублей. Сколько дней (включая сегодняшний) она сможет пользоваться телефоном, не пополняя счет? Ответ: 18. Тема: Практико-ориентированные задачи (2). В магазине вся мебель продается в разобранном виде. Покупатель может заказать сборку мебели на дому, стоимость которой составляет 15% от стоимости купленной мебели. Шкаф стоит 1500 рублей. Во сколько рублей обойдется покупка этого шкафа вместе со сборкой? Ответ: 1725. Флакон шампуня стоит 150 рублей. Какое наибольшее число флаконов можно купить на 900 рублей во время распродажи, когда скидка составляет 15%? Ответ: 7. Цена на электрический чайник была повышена на 18% и составила 1652 рубля. Сколько рублей стоил чайник до повышения цены? Ответ: 1400. Магазин делает пенсионерам скидку на определенное количество процентов от стоимости покупки. Дыня стоит 50 рублей. Пенсионер заплатил за дыню 46 рублей. Сколько процентов составляет скидка для пенсионеров? Ответ: 8. Железнодорожный билет для взрослого стоит 320 рублей. Стоимость билета для школьника составляет 50% стоимости для взрослого. Группа состоит из 19 школьников и 3 взрослых. Сколько рублей стоят билеты на всю группу? Ответ: 4000. Тема: Вероятность. В сборнике билетов по физике всего 25 билетов, в 13 из них встречается вопрос по оптике. Найдите вероятность того, что в случайно выбранном на экзамене билете школьнику не достанется вопроса по оптике. Ответ: 0,48. В классе 6 учащихся, среди них два друга – Сергей и Олег. Учащихся случайным образом разбивают на 2 равные группы. Найдите вероятность того, что Сергей и Олег окажутся в одной группе. Ответ: 0,4. Перед началом первого тура чемпионата по шахматам участников разбивают на игровые пары случайным образом с помощью жребия. Всего в чемпионате участвует 26 шахматистов, среди которых 11 участников из России, в том числе Петр Трофимов. Найдите вероятность того, что в первом туре Петр Трофимов будет играть с каким-либо шахматистом из России. Ответ: 0,4. В случайном эксперименте симметричную монету бросают трижды. Найдите вероятность того, что орел выпадет ровно один раз. Ответ: 0,375. Биатлонист попадает в мишень с вероятностью 0,7. Он стрелял пять раз. Найдите вероятность того, что он не попадет в мишень ни одного раза. Ответ: 0,00243. Тема: Планиметрия. Периметр параллелограмма равен 56. Одна сторона параллелограмма на 3 больше другой. Найдите меньшую сторону параллелограмма. Ответ: 12,5. Средняя линия трапеции равна 35, а меньшее основание равно 27. Найдите большее основание трапеции. Ответ: 43. Гипотенуза прямоугольного треугольника равна 30. Найдите радиус описанной окружности этого треугольника. Ответ: 15. В треугольнике АВС угол С равен 90 градусов, ВС=𝟐√𝟏𝟓 . Радиус описанной окружности этого треугольника равен 8. Найдите АС. Ответ: 14. Периметр четырехугольника, описанного около окружности, равен 74, две его стороны равны 21 и 25. Найдите большую из оставшихся сторон. Ответ: 16. Т 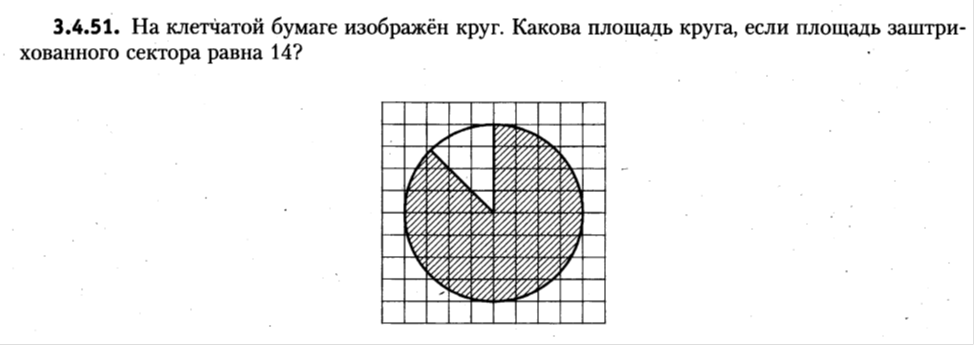 ема: Площадь. ема: Площадь.На клетчатой бумаге изображен круг. Какова площадь круга, если площадь заштрихованного сектора равна14? Ответ: 16. Н 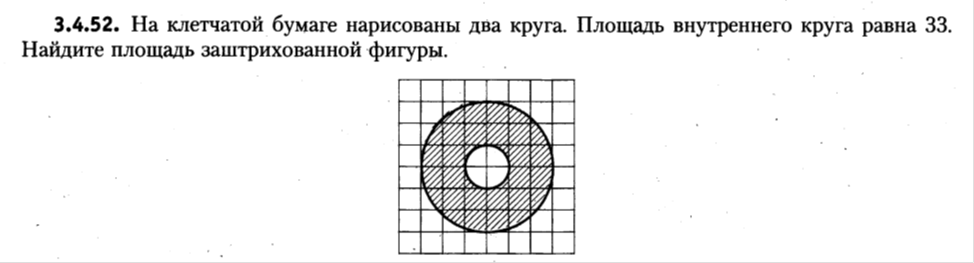 а клетчатой бумаге нарисованы два круга. Площадь внутреннего круга равна 33. Найдите площадь заштрихованной фигуры. а клетчатой бумаге нарисованы два круга. Площадь внутреннего круга равна 33. Найдите площадь заштрихованной фигуры. Ответ: 264. Н 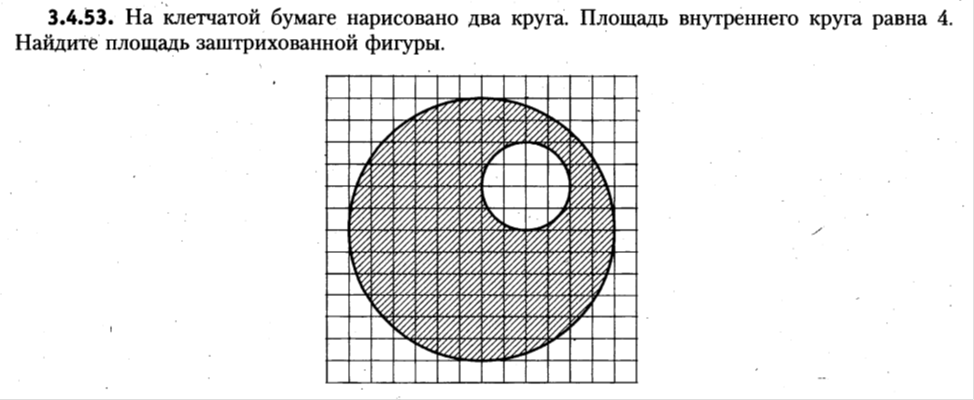 а клетчатой бумаге нарисованы два круга. Площадь внутреннего круга равна 4. Найдите площадь заштрихованной фигуры. а клетчатой бумаге нарисованы два круга. Площадь внутреннего круга равна 4. Найдите площадь заштрихованной фигуры. Ответ: 32. Н  айдите площадь параллелограмма, изображенного на клетчатой бумаге с размером клетки 1см х1 см. Ответ дайте в квадратных сантиметрах. Ответ: 9. айдите площадь параллелограмма, изображенного на клетчатой бумаге с размером клетки 1см х1 см. Ответ дайте в квадратных сантиметрах. Ответ: 9.Найдите площадь круга, длина окружности которого равна √𝝅. Ответ: 0,25. Тема: Стереометрия. Площадь основания конуса равна 81π, высота – 2. Найдите площадь осевого сечения конуса. Ответ: 18. В прямоугольном параллелепипеде АВСDA1B1C1D1 известны длины ребер: АВ=17, AD=15, АА1=8. Найдите площадь сечения параллелепипеда плоскостью, проходящей через точки А, В и С1. Ответ: 289. Длина окружности основания цилиндра равна 3, высота равна 8. Найдите площадь боковой поверхности цилиндра. Ответ: 24. Около шара описан цилиндр, площадь поверхности которого равна 3. Найдите площадь поверхности шара. Ответ: 2. Найдите объем многогранника, вершинами которого являются точки А, В, D, А1, В1 прямоугольного параллелепипеда ABCDA1D1C1D1, у которого АВ=6, AD=5, АА1=4 Ответ: 40. Финальный раунд. Тема: Вклады. В таблице даны условия банковского вклада в трех различных банках. Предполагается, что клиент кладет на счет 15 000 рублей на срок 1 год. В каком банке к концу года вклад окажется наибольшим? В ответе укажите сумму этого вклада в рублях.
Ответ: 15 270. Тема: Вероятность. Две фабрики выпускают одинаковые стекла для автомобильных фар. Первая фабрика выпускает 45% этих стекол, вторая – 55%. Первая фабрика выпускает 5% бракованных стекол, а вторая – 3%. Найдите вероятность того, что случайно купленное в магазине стекло окажется бракованным. Ответ: 0,039. Т 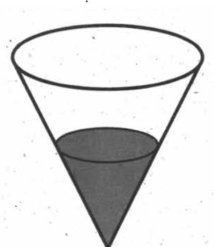 ема: Стереометрия. ема: Стереометрия.В сосуде, имеющем форму конуса, уровень жидкости достигает ½ высоты. Объем жидкости равен 45 мл. Сколько миллилитров жидкости нужно долить, чтобы полностью наполнить сосуд? Ответ: 315. Тема: Наибольшее и наименьшее значения функции. Найдите наибольшее значение функции 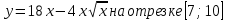 . . Ответ: 54. Тема: Исследование функции. На рисунке изображен график функции у=f(х),определенной на интервале (-4; 10). Определите количество целых точек (координата – целое число), в которых производная функции f(х) отрицательна. 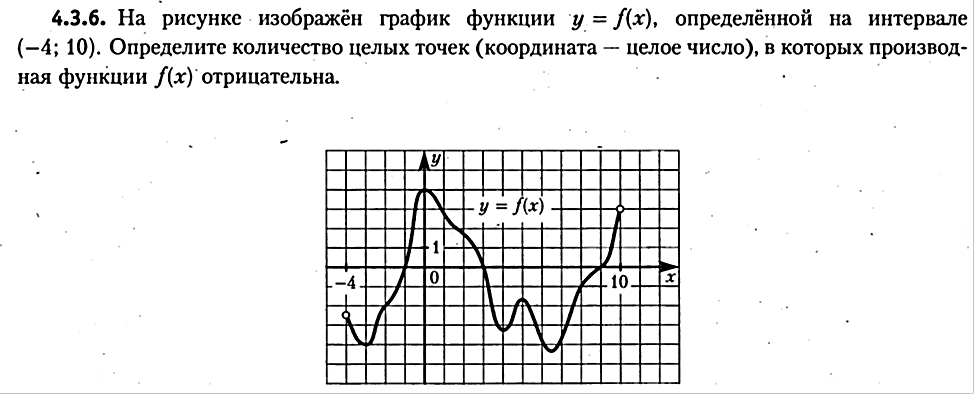 Ответ: 4. |
