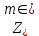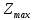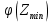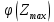Семестровая работа по теме метрология. Волгоградский государственный технический университет
 Скачать 59.39 Kb. Скачать 59.39 Kb.
|
|
Министерство науки и высшего образования Российской Федерации Федеральное государственное бюджетное образовательное учреждение высшего образования «Волгоградский государственный технический университет» ВолгГТУ Химико-технологический факультет Кафедра «Технология машиностроения» Контрольно-семестровая работа по дисциплине метрология, стандартизация и спецификация Вариант - 6 Выполнил: студент группы РХТ-348 Литвинов Проверил: доцент Крайнев Д.В. Волгоград 2019 ВАРИАНТ 6 Обработка результатов равноточных многократных измерений с получением среднего арифметического 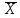 , среднеквадратичного отклонения Sx, и определением суммарной погрешности измерения в виде доверительного интервала – ±∑∆Рд. , среднеквадратичного отклонения Sx, и определением суммарной погрешности измерения в виде доверительного интервала – ±∑∆Рд.Таблица 1.-Исходные данные
РЕШЕНИЕ Определяем величину размаха R (поле рассеяния): R= Xmax – Xmin Xmax =80,23 (мм)– наибольшее из измеренных значений Xmin =79,97 (мм)– наименьшее из измеренных значений R = Xmax – Xmin =80,23-79,97=0,26 (мм). Определяем число интервалов разбиения n: n=N1/2 где N – число измерений; N = 61 n= 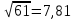 (количество интервалов принимается ближайшим большим нечетным). Принимаем n = 7. Определяем ширину интервала h: 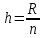 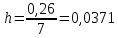 Определим границы интервалов: 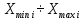 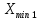 = =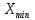 = 79,970 мм = 79,970 мм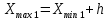 =79,970 +0,0371=80,007мм =79,970 +0,0371=80,007мм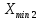 = =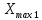 = 80,007 мм = 80,007 мм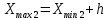 =80,007 +0,0371 =80,044 мм =80,007 +0,0371 =80,044 мм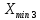 = =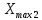 = 80,044 мм = 80,044 мм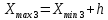 =80,044 +0,0371 =80,081 мм =80,044 +0,0371 =80,081 мм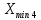 = =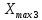 = 80,081мм = 80,081мм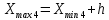 =80,081+0,0371 =80,118 мм =80,081+0,0371 =80,118 мм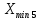 = =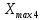 = 80,118мм = 80,118мм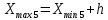 =80,118+0,0371=80,155 мм =80,118+0,0371=80,155 мм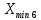 = =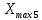 = 80,155 мм = 80,155 мм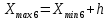 =80,155 +0,0371=80,192мм =80,155 +0,0371=80,192мм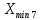 = =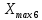 = 80,192мм = 80,192мм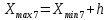 =80,192+ 0,0371= 80,230мм =80,192+ 0,0371= 80,230ммОпределяем середины интервалов ХОi: 1 интервал: ХОi= 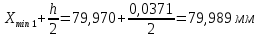 2 интервал: ХОi= 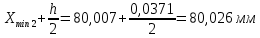 3 интервал: ХОi= 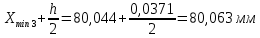 4 интервал: ХОi= 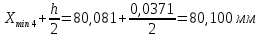 5 интервал: ХОi= 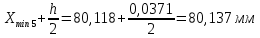 6 интервал: ХОi= 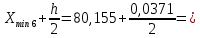 80,174 80,174 7 интервал: ХОi= 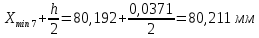 Определение количества размеров попадающих в каждый интервал mi: Используя заданную выборку, подсчитываем количество размеров, попадающих в каждый интервал (если размер совпадает с границей интервала, то его относят в интервал, находящийся слева по числовой оси) Результаты выполненных выше расчетов занесем в таблицу 2: Таблица 2.
 Найдем параметр 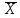 , который является средним арифметическим значение измеряемой величины и определяется по формуле: , который является средним арифметическим значение измеряемой величины и определяется по формуле: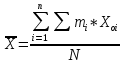 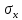 – стандартное отклонение размеров (СКО) совокупности. – стандартное отклонение размеров (СКО) совокупности.Считая, что СКО практически совпадает с его выборочной оценкой ( 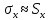 ) приведем формулу, по которой определяется оценка СКО: ) приведем формулу, по которой определяется оценка СКО: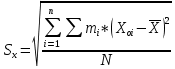 После подстановки получим численные значения среднеарифметического и оценки СКО: 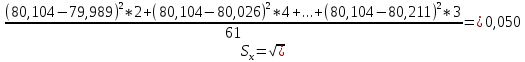  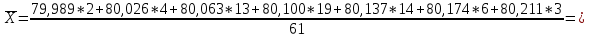 80,104 80,104Построение гистограммы нормального распределения 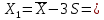 79,954 79,954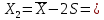 80,004 80,004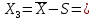 80,054 80,054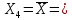 80,104 80,104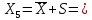 80,154 80,154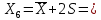 80,204 80,204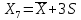 =80,254 =80,254Находим значения функции Лапласа и вычисляем вероятность (учитывая знак -) 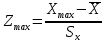 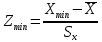 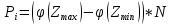 Результаты расчетов сведем в таблицу 3 Таблица 3. Расчет теоретической вероятности Рi
На основании полученных данных выполним рисунок 1 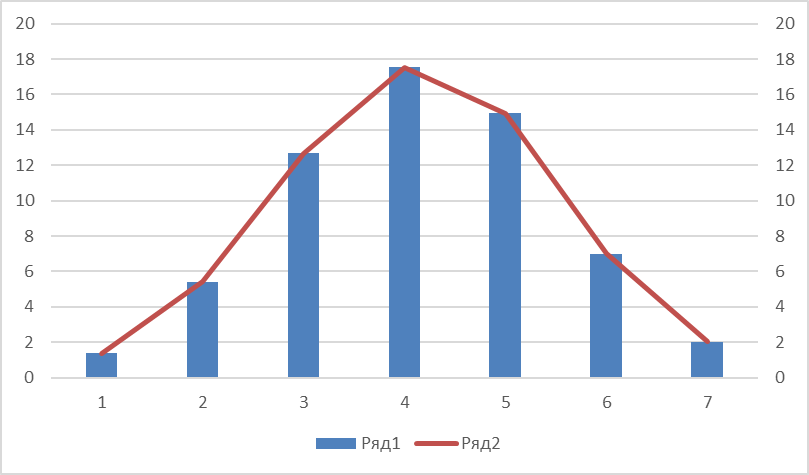 Рисунок 1.Гистограмма и полигон нормального распределения При числе измерений свыше 50 (N=61) проверка распределения на соответствие нормальному закону может выполняться по критерию Пирсона. При использовании этого критерия определяется параметр 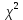 по следующей формуле: по следующей формуле: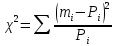 где Рi – теоретическая вероятность попадания в интервал Полученные ранее результаты позволяют получить расчетную величину параметра 𝜒2: 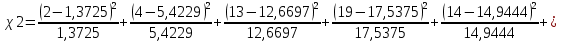 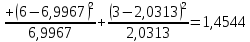 Находим прцент годного и брака выборки Таблица 4 – Результаты расчетов
Годные= Ф(Zmax)(заданные)- Ф(Zmin)(заданные)*100= Брак= (Ф(Zmax)(заданные)-Ф(Zmax)(расчетные))*100+ (Ф(Zmin)(заданные)-Ф(Zmin)(расчетные))*100= Для совпадения фактического закона распределения с теоретическим законом нормального распределения необходимо, чтобы выполнялось следующее условие: 𝜒2 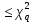 Где 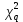 – теоретическое граничное значение параметра 𝜒 2, которое определим cледующим образом: – теоретическое граничное значение параметра 𝜒 2, которое определим cледующим образом:Для получения табличного значения необходимо определиться с двумя параметрами:уровнем значимости q, который показывает вероятность того, что законы не совпадут. В нашем случае, в соответствии с заданием, q = 0,02 (из условия);числом степеней свободы, которое определяется в зависимости от числа интервалов n и числа определяемых по статистике параметров, необходимых для совмещения модели и гистограммы r. Для нормального закона распределения r = 2,так как закон однозначно характеризуется двумя параметрами – СКО и МО (математическим ожиданием). Число степеней свободы определяется по формуле: 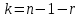 Тогда получаем : 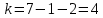 Таким образом, табличное значение 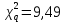 𝜒2 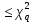 1,4544≤ 9,49 Выполняется закон нормального распределения. | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||