Волгоградский строительный техникум (гбпоу Волгоградский строительный техникум) индивидуальный проект по учебной дисциплине математика

• Название: Волгоградский строительный техникум (гбпоу Волгоградский строительный техникум) индивидуальный проект по учебной дисциплине математика
• Дата: 03.06.2021
• Размер: 0.7 Mb.
• Имя файла: 0007cf30-99bdbd59.doc
• Тип: Реферат; #213563

государственное бюджетное профессиональное образовательное учреждение

«Волгоградский строительный техникум»

(ГБПОУ «Волгоградский строительный техникум»)


ИНДИВИДУАЛЬНЫЙ ПРОЕКТ

по учебной дисциплине

МАТЕМАТИКА
Тема: Лист Мёбиуса и его свойства
Выполнил:

студент гр. Шоп 1-18

Квартин Роман Дмитриевич

Руководитель проекта:

преподаватель

Галушкина Марина Александровна

2019
Содержание

Введение 3

1.2. А.Ф. Мёбиус и его поразительное открытие 5

1.2. Представление о листе Мёбиуса 7

1.3. Применение листа Мёбиуса 8

2. Исследовательская деятельность 10

2.1. Анкетирование студентов 10

2. 2 Практическая часть 12

2.2.1. Изготовление листа Мёбиуса 12

2.2.2. Проведение опытов с листом Мёбиуса 12

Заключение 15

Список литературы 16

Приложение А 17

Приложение Б 18

Приложение В 20

Введение

В наше время актуально изучение различных свойств предметов и их нестандартных применений. Я рассмотрел применение листа Мебиуса в науке и технике. Уже сейчас лента Мебиуса находит различное применение в быту: абразивные ремни для заточки инструментов, красящие ремни для печатающих устройств, ременные передачи, магнитофонные ленты и т.д.

Кроме того, существует гипотеза, что наша Вселенная вполне вероятно замкнута в ту же самую ленту согласно теории относительности – чем больше масса, тем больше кривизна пространства.

Есть гипотеза, что спираль ДНК сама по себе тоже является фрагментом ленты Мебиуса, и только поэтому генетический код так сложен для расшифровки и восприятия[2].

Исходя из вышесказанного, я ставлю перед собой следующие цели:

1. 
   Показать, что лист Мебиуса – модель односторонней поверхности.
   
2. 
   Сформулировать свойства листа Мебиуса.
   
3. 
   Рассмотреть применение листа Мебиуса на практике.
   

Новизна работы заключается в том, что студенты нашего техникума выявлением свойств листа Мёбиуса ранее не занимались. Я провел анкетирование и заметил, что многие не слышали об этом листе ничего и не знают о его свойствах.

Объект исследования: лист Мёбиуса как модель односторонней поверхности.

Предмет исследования: свойства листа Мебиуса.

Поверхность стола, бумаги, поверхность стен комнаты, поверхность земного шара известны всем. Может ли быть что-нибудь неожиданное и даже таинственное в таком обычном понятии? Пример листа Мёбиуса показывает, что может[4].

Исследовательский проект по содержанию является монопредметным (математика), по стилю исполнения межпредметным (математика, информатика).

Основными этапами исследования были:

• 
  постановка проблемы;
  
• 
  анкетирование;
  
• 
  изучение литературы с целью получения информации о листе Мёбиуса;
  
• 
  сбор собственного материала;
  
• 
  проведение экспериментов;
  
• 
  разработка нового электронного продукта.
  

Цель работы: исследовать поверхность листа Мебиуса и его свойства.

Для достижения данной цели я поставил перед собой следующие задачи:

• 
  Познакомиться с биографией Мебиуса и с историей его замечательного открытия.
  
• 
  Описать лист Мёбиуса и процесс его изготовления.
  
• 
  Изучить и исследовать свойства листа Мебиуса
  
• 
  Установить области применения листа Мебиуса.
  
• 
  Создать презентацию в Microsoft Power Point.
  

Гипотеза исследования: Я предполагаю, что лист Мёбиуса действительно обладает неожиданными свойствами.

Для того чтобы решить эту проблему, я должна изучить нужную информацию в математической литературе и на различных сайтах Интернета, затем изготовить лист Мебиуса и с помощью опытов выявить его необыкновенные свойства.

Вид проекта – информационно-исследовательский.

Методы исследования:

• 
  поисковый;
  
• 
  аналитический;
  
• 
  экспериментальный;
  
• 
  описательный
  

Готовый продукт – мультимедийная презентация.

1.2. А.Ф. Мёбиус и его поразительное открытие

Август Фердинанд Мёбиус (1790-1868) – немецкий геометр, ученик «короля математиков». Мёбиус был первоначально астрономом, как Гаусс. В те времена изучение математики не встречало поддержки, а занятие астрономией приветствовалось. С 1816 года начал вести самостоятельные астрономические наблюдения в Плейсенбургской обсерватории, в 1818 г. стал ее директором, позже – профессором Лейципгского университета (Мёбиусу было всего тогда 26 лет). Научные статьи, лекции, работа. Все как у обычного профессора университета. Рассеянного, доброго чудака студенты боготворили. Он мог назначить лекцию на два часа ночи, чтобы показать ночное небо во всей его красе. Занимаясь астрономией, Мёбиус много размышлял о математике.

Одним «неожиданным» математическим открытием является лента Мёбиуса. Рассказывают, что открыть свой  «лист» Мёбиусу помогла служанка, сшившая однажды неправильно концы ленты.

Хмуро разглядывая злосчастную ленту, профессор воскликнул: «Ай да, Марта! Девочка не так уж глупа. Ведь это же односторонняя кольцевая поверхность. У ленточки нет изнанки!»

Мёбиус сделал поразительное открытие – получил поверхность, которая имеет лишь одну сторону (до него считалось, что любая поверхность, например, лист бумаги, имеет две стороны). Открытая поверхность получила математическое обоснование и имя в честь описавшего ее математика и астронома. Лента вдохновила на подвиги не одного добряка-профессора. Взял ее на вооружение и цех парижских портных. Отныне в качестве экзамена для новичка, претендовавшего на зачисление в цех, было пришивание к подолу юбки тесьмы в форме ленты Мебиуса. Оценили по достоинству невольное изобретение Марты и учителя. Неугомонным нерадивым ученикам предлагалось покрасить стороны ленты Мебиуса в разные цвета. Пыхтя от усердия, школяры проводили за этим занятием немало времени[3].

Главная ценность листа Мёбиуса состоит в том, что он дал толчок новым обширным математическим исследованиям. Его часто считают символом современной математики.

1.2. Представление о листе Мёбиуса

Лист Мебиуса положил начало новой науке – топологии. Слово это придумал Иоганн Бенедикт Листинг, профессор Геттингенского университета, который почти в тоже время, что и его лейпцигский коллега, предложил в качестве первого примера односторонней поверхности уже знакомую нам, единожды перекрученную, ленту.

Лист Мёбиуса - бумажная лента, повернутая одним концом на полоборота (то есть на 180 градусов), и склеенная с его другим концом. ( рис. 1)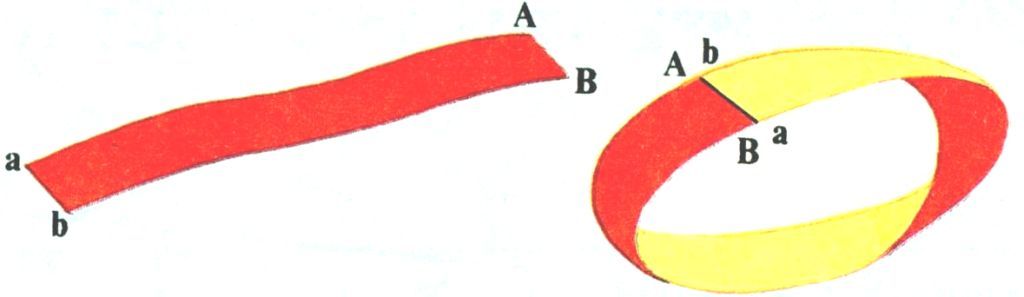



Рисунок 1

Поверхность листа Мёбиуса имеет только одну сторону. Это легко проверить. Возьмите карандаш, и начните закрашивать ленту в каком-нибудь направлении. Вскоре вы вернетесь в то место, откуда начали. А теперь поглядите внимательно: закрашенной оказалась вся лента целиком! А ведь вы ее не переворачивали, чтобы закрасить с другой стороны. Да и не смогли бы перевернуть, даже если бы очень захотели, потому как поверхность ленты Мёбиуса - односторонняя. Такое вот у нее любопытное свойство наблюдается.

Что же из этого свойства следует? А следует удивительное превращение ленты.

Если разрезать ее вдоль, точно посередине - получится не две, а одна лента. А вот если разрезать ленту на расстоянии 1/3 ее ширины от края, то получится два кольца - но!- одно большое и сцепленное с ним маленькое. Если же разрезать еще и маленькое кольцо вдоль посередине, то у вас окажется весьма «затейливое» переплетение двух колец – одинаковых по размеру, но разных по ширине. [1]

1.3. Применение листа Мёбиуса

Удивительные свойства листа Мёбиуса используются в самых различных изобретениях.

В виде парадоксальной геометрической фигуры можно, оказывается, изготовить лопасти бетономешалки или обычного бытового миксера.( рис. 2)



Рисунок 2

Полоса ленточного конвейера выполняется в виде ленты Мёбиуса, что позволяет ему работать дольше, потому, что вся поверхность ленты изнашивается равномерно. Представьте себе обыкновенную ленту, образующую кольцо. На наружную сторону ленты нанесён шлифовальный порошок. Ленту прижимают к изделию, прокручивают, идёт шлифовка. Через какое-то время стирается и сам шлифовальный слой на ленте. Приходится прерывать процесс, менять ленту. В 1969 году изобретателю А. Губайдуллину было выдано авторское свидетельство на шлифовальное устройство с лентой Мёбиуса: срок работы ленты увеличились вдвое.

В технике так же применяется резистор Мебиуса, прокатный стан, ремень передачи, подшипник в виде ленты Мебиуса для увеличения срока работы, ремень передачи.( рис. 3)


Рисунок 3

Благодаря ленте Мёбиуса, были созданы особые кассеты для магнитофона, которые дали возможность слушать магнитофонные кассеты с “двух сторон” не меняя их местами.( рис. 4)



Рисунок 4

В большинстве матричных принтеров красящее устройство также имеет вид листа Мёбиуса для увеличения его ресурса. Архитектурные сооружения имеют вид знаменитой ленты Мёбиуса.

Имеются воплощения простого листа Мёбиуса в строительстве. Построенный в Лондоне велодром имеет контуры, которые можно назвать вариацией на тему листа Мёбиуса.( рис. 5)



Рисунок 5

Международный символ переработки представляет собой Лист Мёбиуса.( рис. 6)


Рисунок 6

Мотив Ленты Мебиуса встречается в названиях художественных произведений, общественных заведений, логотипах, ленту Мёбиуса часто изображают на различных эмблемах и значках.

Например, на значке механико-математического  факультета Московского университета.( рис. 7)



Рисунок 7

Всего в разных странах за последние годы выдано более ста патентов и авторских свидетельств на использование этой удивительной ленты.

2. Исследовательская деятельность

2.1. Анкетирование студентов

Чтобы выяснить, что же знают студенты нашего техникума о листе Мёбиуса и его свойствах, я провел среди них анкетирование.

Анкета содержала следующие вопросы:

Анкета:

Ответьте, пожалуйста, на следующие вопросы:

1. 
   Знаете ли Вы, что такое топология?
   

- нет;

- да.

2. Знакомо ли Вам понятие «Лист Мёбиуса»?

- я знаю, что это такое;

- только слышал о таком понятии;

- не знакомо.

3. Знаете ли Вы о свойствах листа Мёбиуса?

- нет;

- да, это следующие свойства - ______________________.

4. Знаете ли Вы, где применяется Лист Мёбиуса?

- нет;

- да, он применяется - _______________________________.

Обработав анкеты, я получил следующие результаты:

Знают, что такое топология – 8 человек (8 %) (Диаграмма – рис. 8)



Рисунок 8
Знают, что такое лист Мёбиуса – 5 человек (5 %)

Только слышали о листе Мёбиуса – 14 человек (14%)

Не знакомо – 81 человек (81%) (диаграмма – рис.9)



Рисунок 9

Знают о свойствах листа Мёбиуса – 4 человека (4%) (диаграмма – рис.10)



Рисунок 10

Знают, где применяется лист Мёбиуса – 4 человека (4%) (диаграмма – рис. 11)



Рисунок 11

Анкетирование показало, что большинству опрошенных не знаком лист Мёбиуса и всё, что с ним связано.

2. 2 Практическая часть

2.2.1. Изготовление листа Мёбиуса

Берём бумажную ленту АВВ₁А₁. Прикладываем её концы АВ и А₁В₁ друг к другу и склеиваем. Но не как попало, а так, чтобы точка А совпала с точкой В₁, а точка В с точкой А₁. (склеим концы ленты, предварительно повернув один из них на 180 градусов). Получим перекрученное кольцо. Лист Мёбиуса готов.

2.2.2. Проведение опытов с листом Мёбиуса

Для проведения опытов я изготовил бумажные полосы длиной 30 см и шириной 3 см. Чтобы понять, в чём особенность листа Мёбиуса, я проводил опыты с обычным бумажным кольцом и с перекрученным (листом Мёбиуса).

Таблица 1

Опыт 1	Поставим точку на одной стороне каждого кольца и начертим непрерывную линию вдоль него, пока не придём снова в отмеченную точку.
Обычное кольцо ( рис. 12) Линия проходит вдоль кольца по одной стороне, сходясь в точке начала. Вторая остаётся чистой. Рисунок 12		Лист Мёбиуса ( рис. 13) Непрерывная линия проходит по двум сторонам, заканчиваясь в начальной точке. Рисунок 13

Вывод: Поверхность листа Мёбиуса является непрерывной.

На листе Мёбиуса любая точка может быть соединена с любой другой точкой и при этом ни разу не придётся «переползать» через край ленты. Разрывов нет – непрерывность полная.

Таблица 2

Опыт 2	Закрасим полностью только одну сторону колец.
Обычное кольцо ( рис. 14) Одна сторона закрашена, другая нет. Рисунок 14		Лист Мёбиуса ( рис. 15) Закрашенной оказалась весь лист целиком. Рисунок 15

Вывод: Поверхность листа Мёбиуса односторонняя.

Лист оказался закрашенным полностью! А ведь мы его даже не переворачивали, чтобы закрасить с другой стороны. Да и не смогли бы перевернуть, даже если бы очень захотели. Лист Мёбиуса имеет одну поверхность. «Внешняя» и «внутренняя» стороны как бы по ходу движения вдоль ленты переходят друг в друга.

Опыт 3	Закрасим непрерывной линией только один край колец
Обычное кольцо (рис. 16) Один край кольца закрашен, второй край нет. Рисунок 16		Лист Мёбиуса(рис. 17) Линия края получилась, непрерывно закрашена на всём кольце. Рисунок 17

Вывод: У листа Мёбиуса не только одна сторона, но и только один край.

Заключение

Выполняя работу по изучению удивительного листа Мёбиуса, я узнал о жизни самого учёного, об истории уникального открытия. Не зря говорят: «Всё гениальное рядом». Открытие положило начало новому направлению в математике. Мною была изучена большая разнообразная информация. Она анализировалась и перерабатывалась.

Я получил удовольствие, когда выполняла опыты. Результаты были очевидны, поскольку эксперименты проводились с обычным кольцом и листом Мёбиуса. Так я узнал об удивительных свойствах листа Мёбиуса. Для меня это были маленькие открытия.

Я сумел получить интересный математический материал. В ходе работы я создал мультимедийную презентацию, в которые включены иллюстративные материалы о листе Мёбиуса. Своими результатами исследования о листе Мебиуса я поделилась со своими друзьями. Думаю, что это их заинтересовало. Я считаю, что моя работа будет интересна любителям математики для расширения математического кругозора. Ее можно использовать учителям математики, как на занятиях, так и во внеклассной и кружковой работе.

С листом Мёбиуса можно провести ещё много опытов и убедиться в открытых свойствах. Количество опытов зависит от собственного интереса и терпения.

Мною не исчерпаны опыты с листом Мебиуса. Они бесконечны, интересны и зависят от собственного терпения. Я обязательно буду возвращаться к опытам с листом Мебиуса.

Список литературы

1. 
   Гарднер М.О.. Математические чудеса и тайны. – М.:Наука,1978.-185 с.;
   
2. 
   Лэнгдон Н., Снейт Ч.. С математикой в путь. – М.: Педагогика, 1987.-113 с.;
   
3. 
   Нагибин Ф.Ф., Канин Е.С.. Математическая шкатулка. – М.: Просвещение, 1988. .-167 с.;
   
4. 
   Смирнова Е.С. Курс наглядной геометрии: Методическая разработка для 6 кл.: Кн.для учителя. – М.:Просвещение, 2002.-198 с.;
   
5. 
   Шарыгин И.Ф., Еранжиева Л.Н. Наглядная геометрия: 5-6 кл. – М.: Дрофа, 2000. .-204 с.;
   

Приложение А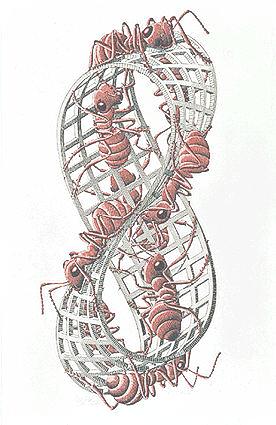

Рисунок 18

Мауриц Эшер.

Гравюра с изображением муравья, ползающего по Ленте Мебиуса.

Приложение Б

Эксперименты с бумагой

Эксперимент 1.Перед склеиванием концов бумажной полосы прорежем щель в полосе, проденем сквозь нее один из ее концов, а затем продолжим разрез вдоль всей ленты.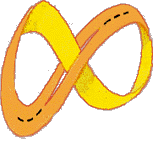



Рисунок 19

Результат: два листа Мебиуса.

Эксперимент 2. Приготовим два кольца: одно обычное и одно Мебиусово. Склеим их под прямым углом, а затем оба разрежем вдоль.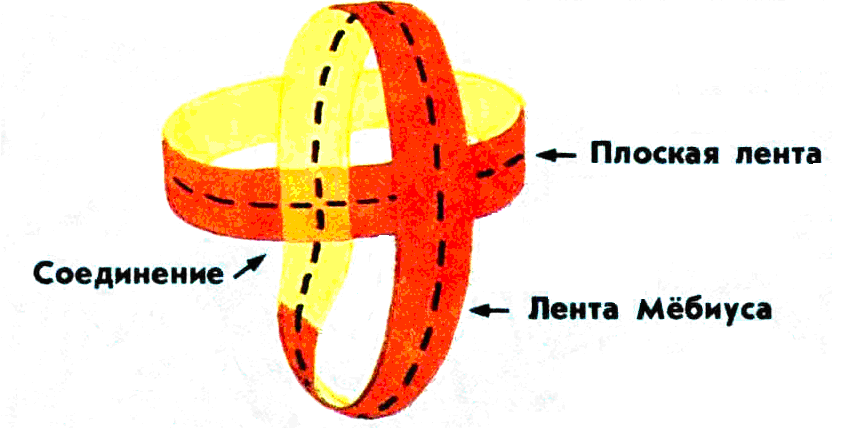



Рисунок 20

Результат: прямоугольная плоская рамка.

Эксперимент 3. Возьмем бумажную полоску. Ее концы перед склеиванием разрежем и перекрутим так, как это показано на рисунке.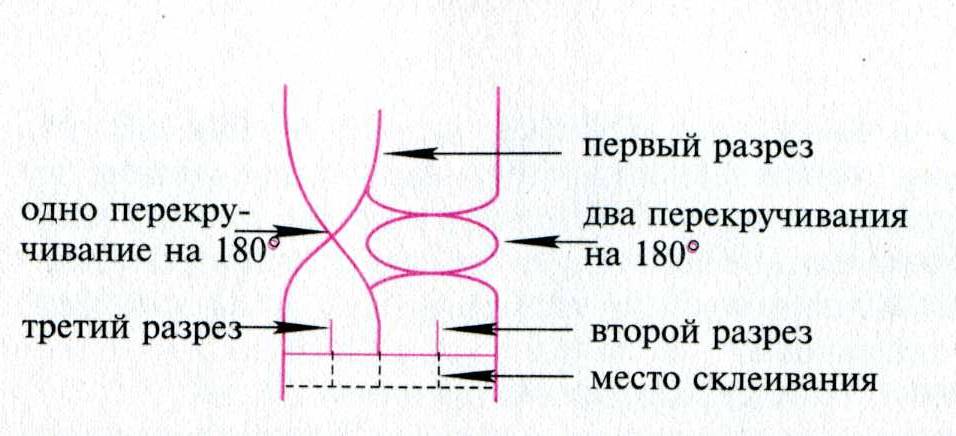



Рисунок 21

Каждая половинка концов перекручивается по-разному, и после склеивания концов выполняются два разреза по средней линии каждой половины бумажной полосы.

Результат: бумажное кольцо распадется на два отдельных кольца, одно из которых при разрезании посредине превращается в два отдельных кольца, а другое — в одно большое.

Эксперимент 4. Трижды перекрученную бумажную ленту проденем сквозь перстень, склеим концы, а затем разрежем по средней линии.

Результат: одно большое бумажное кольцо с узлом, завязанным вокруг перстня.

Приложение В

Анкета:

Ответьте, пожалуйста, на следующие вопросы:

1. 
   Знаете ли Вы, что такое топология?
   

- нет;

- да.

2. Знакомо ли Вам понятие «Лист Мёбиуса»?

- я знаю, что это такое;

- только слышал о таком понятии;

- не знакомо.

3. Знаете ли Вы о свойствах листа Мёбиуса?

- нет;

- да, это следующие свойства - ______________________.

4. Знаете ли Вы, где применяется лист Мёбиуса?

- нет;

- да, он применяется - _______________________________.