Вопрос 1 Матрицы и многомерные векторы
 Скачать 0.91 Mb.
|
|
Векторы и линейные операции над ними. Линейными операциями над векторами называется сложение и умножение на число. Суммой двух векторов a и b называется вектор c, направленный из начала вектора a в конец вектора b при условии, что начало b совпадет с концом вектора a. Если векторы заданы их разложениями по базисным ортам, то при сложении векторов складываются их соответствующие координаты. Сумма любого конечного числа векторов может быть найдена по правилу многоугольника: чтобы построить сумму конечного числа векторов, достаточно совместить начало каждого последующего вектора с концом предыдущего и построить вектор, соединяющий начало первого вектора с концом последнего. Разностью векторов a и b называют вектор a+(-b). Второе слагаемое является вектором, противоположным вектору b по направлению, но равным ему по длине. Длина вектора. Длиной (модулем) вектора называется расстояние между началом и концом вектора. Вопрос №13 Координаты на прямой. Упорядоченная тройка некомпланарных векторов e1, e2, e3 называется базисом в множестве всех геометрических векторов. Всякий геометрический вектор a может быть единственным образом представлен в виде a=x1e1+x2e2+x3e3 числа x1 , x2 , x3 называют координатами вектора а в базисе (e1, e2, e3). Деление отрезка в данном отношении  . В координатах:на прямой  ; на плоскости ,  ; в пространстве , ,  .Вопрос №14 Декартовы прямоугольные координаты на плоскости и в пространстве. Системы координат на плоскости. Д 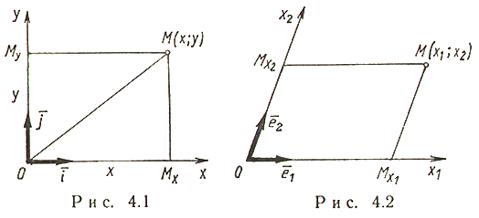 екартовы прямоугольные координаты (рис. 4.1). О - начало координат, Ох - ось абсцисс, Оy - ось ординат,  - базисные векторы,  - абсцисса точки M ( - проекция точки M на ось Ох параллельно оси Оy),  - ордината точки M ( - проекция точки M на ось Oy параллельно оси Ox).Системы координат в пространстве. 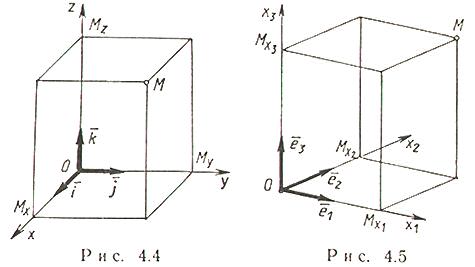Д  екартовы прямоугольные координаты (рис. 4.4). О - начало координат, Ох - ось абсцисс, Оy - ось ординат, Оz - ось аппликат  , - базисные векторы. 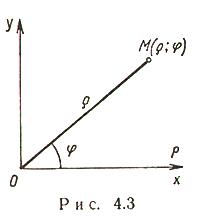Oxy, Oxz, Oyz - координатные плоскости, - абсцисса точки M ( - проекция точки M на ось Ох параллельно плоскости Оyz), - ордината точки M ( - проекция точки M на ось Oy параллельно плоскости Oxz),  - ордината точки M ( - проекция точки M на ось Oz параллельно плоскости Oxy).Вопрос №15 П  олярные координаты на плоскости. О - полюс, Ox - полярная ось,  - полярный радиус,  - полярный угол. Главные значения  и :  (иногда  ).Выражение декартовых прямоугольных координат через полярные:   Выражение полярных координат через декартовы прямоугольные:  С 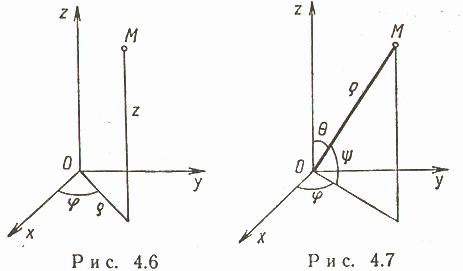 ферические и цилиндрические координаты в пространстве. Цилиндрические координаты. Главные значения , ,  :  Связь между декартовыми прямоугольными и цилиндрическими координатами:  С ферические координаты. Главные значения , ,  :  Иногда вместо рассматривают  :  Вопрос №16 Проекции векторов. Обозначения:  - п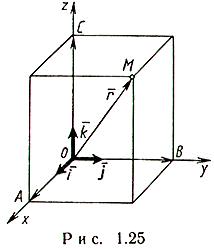роекции вектора  на ось l;  - величина проекции вектора на ось l. Свойства проекций:     С  оставляющие (компоненты) вектора  :     Координаты вектора :    ( - углы, образуемые вектором с положительными направлениями осей координат Ox, Oy, Oz прямоугольной декартовой системы координат).,  ,  называются направляющими косинусами вектора     где  Если  - единичный вектор в направлении , то  Вопрос №17 Линейная зависимость векторов. Векторы  называются линейно зависимыми, если существует такая линейная комбинация  , при не равных нулю одновременно ai, т.е.  . Если же только при ai = 0 выполняется , то векторы называются линейно независимыми. Свойство 1. Если среди векторов есть нулевой вектор, то эти векторы линейно зависимы. Свойство 2. Если к системе линейно зависимых векторов добавить один или несколько векторов, то полученная система тоже будет линейно зависима. Свойство 3. Система векторов линейно зависима тогда и только тогда, когда один из векторов раскладывается в линейную комбинацию остальных векторов. Свойство 4. Любые 2 коллинеарных вектора линейно зависимы и, наоборот, любые 2 линейно зависимые векторы коллинеарны. Свойство 5. Любые 3 компланарных вектора линейно зависимы и, наоборот, любые 3 линейно зависимые векторы компланарны. Свойство 6. Любые 4 вектора линейно зависимы. Условия коллинеарности, ортогональности и компланарности векторов. Векторы, расположенные на одной прямой или на параллельных прямых, называются коллинеарными. Векторы называются ортогональными, если их скалярное произведение равно нулю. Векторы, лежащие в одной плоскости или параллельные одной плоскости, называются компланарными. Вопрос №18 Преобразование декартовой прямоугольной системы координат на плоскости. Параллельный сдвиг координатных осей. 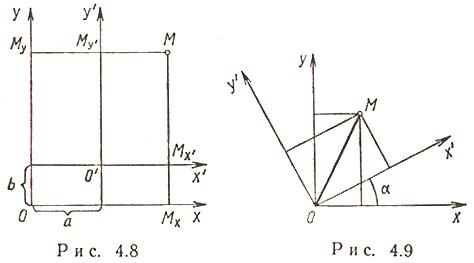  П оворот координатных осей. Параллельный сдвиг и поворот координат осей. 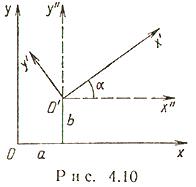  Вопрос №19 Скалярное произведение и его свойства. Скалярным произведением двух векторов называется число, равное произведению длин этих векторов на косинус угла между ними, т.е.  Из определения следует  где φ - угол между векторами. Скалярная величина  называется проекцией вектора  на вектор  .В зависимости от значения угла между векторами, проекция может принимать отрицательные, положительные или нулевое значения. Теперь можно написать  . Из определения скалярного произведения следует, что если векторы ортогональны, то  (условие ортогональности ненулевых векторов).Свойства скалярного произведения.  Вопрос №20 Векторное произведение векторов. У 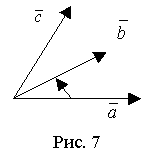 порядоченная тройка векторов  называется правой, если наблюдателю, находящемуся на конце вектора, кратчайший поворот от к кажется происходящим против часовой стрелки. В противном случае тройка векторов левая.Векторным произведением вектора на вектор называется третий вектор  , определяемый следующим образом:1) длина его равна площади параллелограмма, построенного на векторах и , т.е.  где φ - угол между векторами и ;2) вектор  перпендикулярен векторам и ;3) векторы после приведения к общему началу образуют правую тройку векторов.Свойства векторного произведения  |