Множественная регрессия. Два вопроса Регрессия. Вопрос 1 Задача 2
 Скачать 120.29 Kb.
|
|
Проверка гипотез относительно коэффициентов линейного уравнения регрессии. 1) t-статистика. Критерий Стьюдента. С помощью МНК мы получили лишь оценки параметров уравнения регрессии, которые характерны для конкретного статистического наблюдения (конкретного набора значений x и y). Для оценки статистической значимости коэффициентов регрессии и корреляции рассчитываются t-критерий Стьюдента и доверительные интервалы каждого из показателей. Выдвигается гипотеза Н0 о случайной природе показателей, т.е. о незначимом их отличии от нуля. Чтобы проверить, значимы ли параметры, т.е. значимо ли они отличаются от нуля для генеральной совокупности используют статистические методы проверки гипотез. В качестве основной (нулевой) гипотезы выдвигают гипотезу о незначимом отличии от нуля параметра или статистической характеристики в генеральной совокупности. Наряду с основной (проверяемой) гипотезой выдвигают альтернативную (конкурирующую) гипотезу о неравенстве нулю параметра или статистической характеристики в генеральной совокупности. Проверим гипотезу H0 о равенстве отдельных коэффициентов регрессии нулю (при альтернативе H1 не равно) на уровне значимости α=0.05. H0: b = 0, то есть между переменными x и y отсутствует линейная взаимосвязь в генеральной совокупности; H1: b ≠ 0, то есть между переменными x и y есть линейная взаимосвязь в генеральной совокупности. В случае если основная гипотеза окажется неверной, мы принимаем альтернативную. Для проверки этой гипотезы используется t-критерий Стьюдента. Найденное по данным наблюдений значение t-критерия (его еще называют наблюдаемым или фактическим) сравнивается с табличным (критическим) значением, определяемым по таблицам распределения Стьюдента (которые обычно приводятся в конце учебников и практикумов по статистике или эконометрике). Табличное значение определяется в зависимости от уровня значимости (α) и числа степеней свободы, которое в случае линейной парной регрессии равно (n-2), n-число наблюдений. Если фактическое значение t-критерия больше табличного (по модулю), то основную гипотезу отвергают и считают, что с вероятностью (1-α) параметр или статистическая характеристика в генеральной совокупности значимо отличается от нуля. Если фактическое значение t-критерия меньше табличного (по модулю), то нет оснований отвергать основную гипотезу, т.е. параметр или статистическая характеристика в генеральной совокупности незначимо отличается от нуля при уровне значимости α.   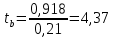 Поскольку 4.37 > 2.634, то статистическая значимость коэффициента регрессии b подтверждается (отвергаем гипотезу о равенстве нулю этого коэффициента).  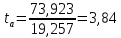 Поскольку 3.84 > 2.634, то статистическая значимость коэффициента регрессии a подтверждается (отвергаем гипотезу о равенстве нулю этого коэффициента). 2) F-статистика. Критерий Фишера. Коэффициент детерминации R2 используется для проверки существенности уравнения линейной регрессии в целом. Проверка значимости модели регрессии проводится с использованием F-критерия Фишера, расчетное значение которого находится как отношение дисперсии исходного ряда наблюдений изучаемого показателя и несмещенной оценки дисперсии остаточной последовательности для данной модели. Если расчетное значение с k1=(m) и k2=(n-m-1) степенями свободы больше табличного при заданном уровне значимости, то модель считается значимой.  где m – число факторов в модели. Оценка статистической значимости парной линейной регрессии производится по следующему алгоритму: 1. Выдвигается нулевая гипотеза о том, что уравнение в целом статистически незначимо: H0: R2=0 на уровне значимости α. 2. Далее определяют фактическое значение F-критерия:  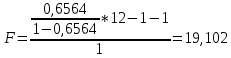 3. Табличное значение определяется по таблицам распределения Фишера для заданного уровня значимости, принимая во внимание, что число степеней свободы для общей суммы квадратов (большей дисперсии) равно 1 и число степеней свободы остаточной суммы квадратов (меньшей дисперсии) при линейной регрессии равно n-2. Fтабл - это максимально возможное значение критерия под влиянием случайных факторов при данных степенях свободы и уровне значимости α. Уровень значимости α - вероятность отвергнуть правильную гипотезу при условии, что она верна. Обычно α принимается равной 0,05 или 0,01. 4. Если фактическое значение F-критерия меньше табличного, то говорят, что нет основания отклонять нулевую гипотезу. В противном случае, нулевая гипотеза отклоняется и с вероятностью (1-α) принимается альтернативная гипотеза о статистической значимости уравнения в целом. Табличное значение критерия со степенями свободы  Поскольку фактическое значение 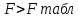 , то коэффициент детерминации статистически значим (найденная оценка уравнения регрессии статистически надежна). Значимость коэффициента корреляции. Выдвигаем гипотезы: H0: rxy = 0, нет линейной взаимосвязи между переменными; H1: rxy ≠ 0, есть линейная взаимосвязь между переменными; Для того чтобы при уровне значимости α проверить нулевую гипотезу о равенстве нулю генерального коэффициента корреляции нормальной двумерной случайной величины при конкурирующей гипотезе H1 ≠ 0, надо вычислить наблюдаемое значение критерия (величина случайной ошибки) 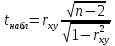 и по таблице критических точек распределения Стьюдента, по заданному уровню значимости α и числу степеней свободы k = n - 2 найти критическую точку 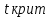 двусторонней критической области. Если tнабл < tкрит оснований отвергнуть нулевую гипотезу. Если 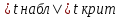 — нулевую гипотезу отвергают.  По таблице Стьюдента с уровнем значимости α=0.05 и степенями свободы k=10 находим tкрит: где m = 1 - количество объясняющих переменных. Если 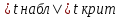, то полученное значение коэффициента корреляции признается значимым (нулевая гипотеза, утверждающая равенство нулю коэффициента корреляции, отвергается). Поскольку 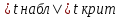, то отклоняем гипотезу о равенстве 0 коэффициента корреляции. Другими словами, коэффициент корреляции статистически - значим Выполним прогноз заработной платы при прогнозном значении среднедушевого прожиточного минимума x, составляющем 107% от среднего уровня. Экономическое прогнозирование на основе построенной модели предполагает, что сохраняются ранее существовавшие взаимосвязи переменных и на период упреждения. Для прогнозирования зависимой переменной результативного признака необходимо знать прогнозные значения всех входящих в модель факторов. Прогнозные значения факторов подставляют в модель и получают точечные прогнозные оценки изучаемого показателя. 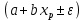 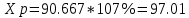 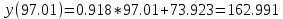 Оценим точность прогноза, рассчитав ошибку прогноза и его доверительный интервал. Рассчитаем границы интервала, в котором будет сосредоточено 95% возможных значений Y при неограниченно большом числе наблюдений и Xp = 97.01 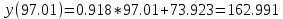Вычислим ошибку прогноза для уравнения 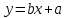 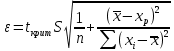 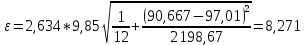 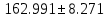 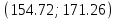 С вероятностью 95% можно гарантировать, что значение Y при x=97.01 будет находиться в интервале от 154.72 до 154.72. Вычислим ошибку прогноза для уравнения   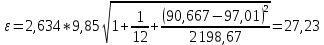   Индивидуальные доверительные интервалы для Y при данном значении X. 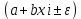 где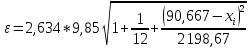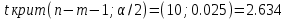   
С вероятностью 95% можно гарантировать, что значения Y при неограниченно большом числе наблюдений не выйдет за пределы найденных интервалов. На одном графике отложим исходные данные и теоретическую прямую.  Проверим вычисления в MS Excel и прикрепим к нашей задаче. Файл приложен. 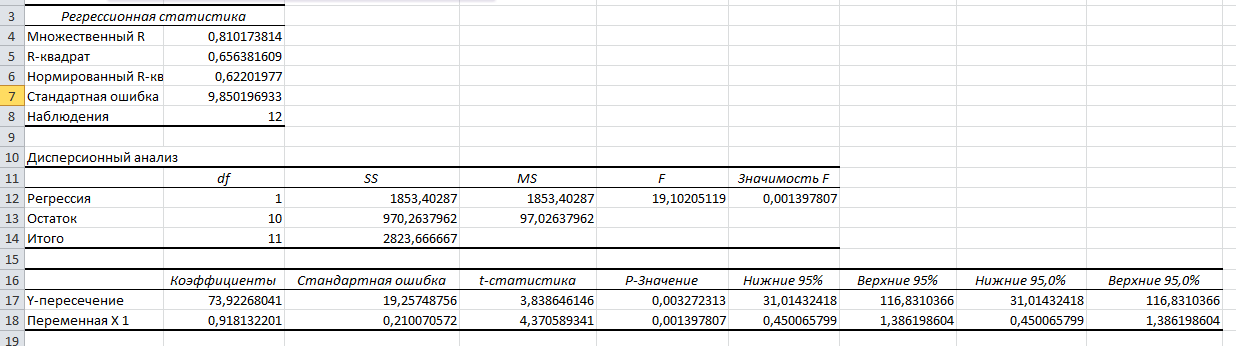 |