Множественная регрессия. Два вопроса Регрессия. Вопрос 1 Задача 2
 Скачать 120.29 Kb. Скачать 120.29 Kb.
|
|
Стандартизированное уравнение множественной регрессии. Коэффициенты 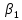 и и 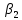 стандартизированного уравнения стандартизированного уравнения 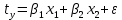 находятся по формулам: находятся по формулам: 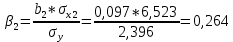 То есть, уравнение будет выглядеть следующим образом: 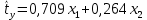 Так как, стандартизированные коэффициенты регрессии можно сравнивать между собой, то можно сказать, что ввод в действие новых основных фондов оказывает большее влияние на выработку продукции, чем удельный вес рабочих высокой квалификации. Коэффициенты парной, частой и множественной корреляции. Коэффициенты парной корреляции мы уже нашли:  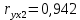  Они указывают на весьма сильную связь каждого фактора с результатом, а также высокую меж-факторную зависимость (факторы х1 и х2 явно коллинеарные, так как  ). При такой сильной меж-факторной зависимости рекомендуется один из факторов исключить из рассмотрения. ). При такой сильной меж-факторной зависимости рекомендуется один из факторов исключить из рассмотрения.Частные коэффициенты корреляции: При двух факторах частные коэффициенты корреляции рассчитываются следующим образом:  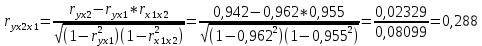 Если сравнить коэффициенты парной и частной корреляции, то можно увидеть, что из-за высокой меж-факторной зависимости коэффициенты парной корреляции дают завышенные оценки тесноты связи. Именно по этой причине рекомендуется при наличии сильной взаимосвязи факторов исключать из исследования тот фактор, у которого теснота парной зависимости меньше, чем теснота меж-факторной связи. Коэффициент множественной корреляции. Формула:  Коэффициент множественной корреляции показывает на весьма сильную связь всего набора факторов с результатом. Нескорректированный коэффициент множественной детерминации 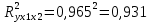 оценивает долю вариации результата за счет представленных в уравнении факторов в общей вариации результата. Здесь эта доля составляет 96,5% и указывает на высокую степень обусловленности вариации результата вариацией факторов, иными словами – на весьма тесную связь фактора с результатом. оценивает долю вариации результата за счет представленных в уравнении факторов в общей вариации результата. Здесь эта доля составляет 96,5% и указывает на высокую степень обусловленности вариации результата вариацией факторов, иными словами – на весьма тесную связь фактора с результатом.Скорректированный коэффициент множественной детерминации:  Определяет тесноту связи с учетом степеней свободы общей и остаточной дисперсий. Он дает такую оценку тесноты связи, которая не зависит от числа факторов и поэтому может сравниваться по разным моделям с разным числом факторов. Оба коэффициента указывают на высокую (более 90%) детерминированность результата у в модели факторами х1 и х2. Критерий Фишера. Оценку надежности уравнения регрессии в целом и показателя тесноты связи 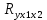 дает F – критерий Фишера: дает F – критерий Фишера: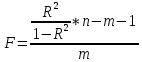 В нашем случае, фактическое значение F – критерия Фишера:  Получили, что  , то есть вероятность случайно получить такое значение F – критерия не превышает допустимый уровень значимости 5%. Следовательно, полученное значение не случайно, оно сформировалось под влиянием существенных факторов, то есть подтверждается статистическая значимость всего уравнения и показателя тесноты связи , то есть вероятность случайно получить такое значение F – критерия не превышает допустимый уровень значимости 5%. Следовательно, полученное значение не случайно, оно сформировалось под влиянием существенных факторов, то есть подтверждается статистическая значимость всего уравнения и показателя тесноты связи 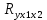 . .С помощью частных F – критериев Фишера оценим целесообразность включения в уравнение множественной регрессии фактора х1 после х2 и фактора х2 после х1 при помощи формул: 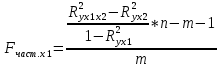 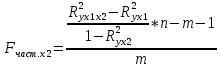 Найдем 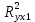 и и   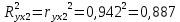 Тогда: 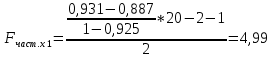 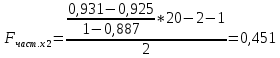 Получили, что  . Следовательно, включение в модель фактора х2, после того, как в модель включен фактор х1 статистически нецелесообразно: прирост факторной дисперсии за счет дополнительного признака х2 оказывается незначительным, несущественным; фактор х2 включать в уравнение после фактора х1 не следует. . Следовательно, включение в модель фактора х2, после того, как в модель включен фактор х1 статистически нецелесообразно: прирост факторной дисперсии за счет дополнительного признака х2 оказывается незначительным, несущественным; фактор х2 включать в уравнение после фактора х1 не следует.Если поменять первоначальный порядок включения факторов в модель и рассмотреть вариант включения х1 после х2, то результат расчета частного F – критерия для х1 будет иным. 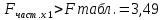 , то есть вероятность его случайного формирования меньше принятого стандарта , то есть вероятность его случайного формирования меньше принятого стандарта 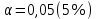 . .Следовательно, значение частного F – критерия для дополнительно включенного фактора х1 не случайно, является статистически значимым, надежным, достоверным: прирост факторной дисперсии за счет дополнительного признака х1 является существенным. Фактор х1 должен присутствовать в уравнении, в том числе в варианте, когда он дополнительно включается после фактора х2. Общий вывод состоит в том, что множественная модель с факторами х1 и х2 с 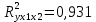 содержит неинформативный фактор х2. Если исключить фактор х2, то можно ограничиться уравнением парной регрессии: содержит неинформативный фактор х2. Если исключить фактор х2, то можно ограничиться уравнением парной регрессии: Проверим вычисления в MS Excel и прикрепим в нашу задачу. Файл приложен к контрольной работе. 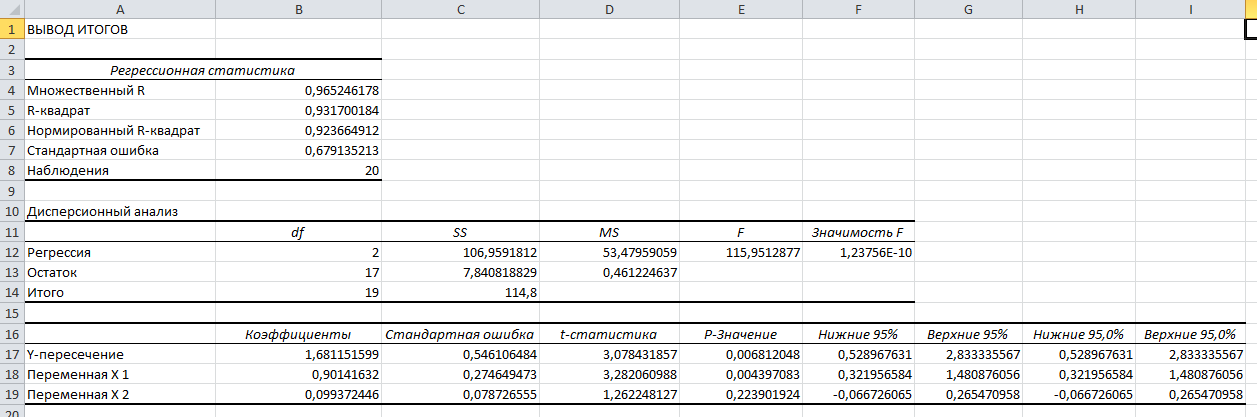 Вопрос 2 Задача 1. По территориям региона приводятся данные за 199X г. (р 1 –число букв в полном имени, р 2 – число букв в фамилии):
Требуется: 1. Построить линейное уравнение парной регрессии y по x. 2. Рассчитать линейный коэффициент парной корреляции, коэффициент детерминации и среднюю ошибку аппроксимации. 3. Оценить статистическую значимость уравнения регрессии в целом и отдельных параметров регрессии и корреляции с помощью F-критерия Фишера и t-критерия Стьюдента. 4. Выполнить прогноз заработной платы при прогнозном значении среднедушевого прожиточного минимума x, составляющем 107% от среднего уровня. 5. Оценить точность прогноза, рассчитав ошибку прогноза и его доверительный интервал. 6. На одном графике отложить исходные данные и теоретическую прямую. 7. Проверить вычисления в MS Excel. Решение: Линейное уравнение регрессии. Для оценки параметров α и β - используют МНК (метод наименьших квадратов). Метод наименьших квадратов дает наилучшие (состоятельные, эффективные и несмещенные) оценки параметров уравнения регрессии. Но только в том случае, если выполняются определенные предпосылки относительно случайного члена (ε) и независимой переменной (x). Формально критерий МНК можно записать так: 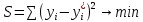 Система нормальных уравнений. 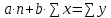 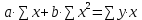 Для расчета параметров регрессии построим расчетную таблицу (табл. 1)
Для наших данных система уравнений имеет вид   Домножим уравнение (1) системы на (-90.667), получим систему, которую решим методом алгебраического сложения.  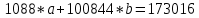 Получаем: 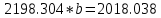 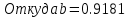 Теперь найдем коэффициент «a» из уравнения (1):   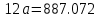 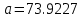 Получаем эмпирические коэффициенты регрессии: 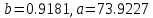 Уравнение регрессии (эмпирическое уравнение регрессии): 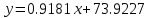 Коэффициенты парной корреляции, детерминации и ошибка аппроксимации. Параметры уравнения регрессии. Выборочные средние:     Выборочные дисперсии:  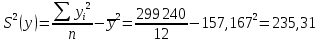 Среднеквадратическое отклонение: 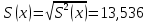 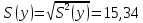 Рассчитываем показатель тесноты связи. Таким показателем является выборочный линейный коэффициент корреляции, который рассчитывается по формуле: 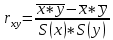 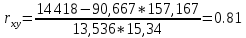 Линейный коэффициент корреляции принимает значения от –1 до +1. Связи между признаками могут быть слабыми и сильными (тесными). Их критерии оцениваются по шкале Чеддока: 0.1 < rxy < 0.3: слабая; 0.3 < rxy < 0.5: умеренная; 0.5 < rxy < 0.7: заметная; 0.7 < rxy < 0.9: высокая; 0.9 < rxy < 1: весьма высокая; В нашем примере связь между признаком Y и фактором X высокая и прямая. Квадрат (множественного) коэффициента корреляции называется коэффициентом детерминации, который показывает долю вариации результативного признака, объясненную вариацией факторного признака. Чаще всего, давая интерпретацию коэффициента детерминации, его выражают в процентах. R2= 0.812 = 0.6564 т.е. в 65.64% случаев изменения х приводят к изменению y. Другими словами - точность подбора уравнения регрессии - средняя. Оценим качество уравнения регрессии с помощью ошибки абсолютной аппроксимации. Средняя ошибка аппроксимации - среднее отклонение расчетных значений от фактических: 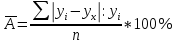 Ошибка аппроксимации в пределах 5%-7% свидетельствует о хорошем подборе уравнения регрессии к исходным данным. 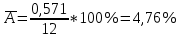 В среднем, расчетные значения отклоняются от фактических на 4.76%. Поскольку ошибка меньше 7%, то данное уравнение можно использовать в качестве регрессии. Оценим статистическую значимость уравнения регрессии в целом и отдельных параметров регрессии и корреляции с помощью F-критерия Фишера и t-критерия Стьюдента. |
