экзмен 26.11. Вопрос 1535324,48 Вопрос 1843. 55
 Скачать 55.14 Kb. Скачать 55.14 Kb.
|
|
Вопрос 1. 1535324,48 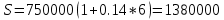 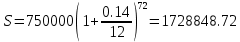 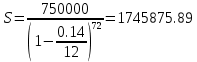 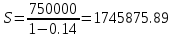 Вопрос 2. 1843.55 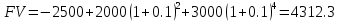 Вопрос 3. 967,07 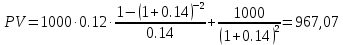 Вопрос 4. -2000  Вопрос 5 – 4,55 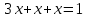 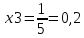 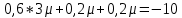 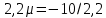 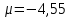 Вопрос 6.  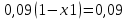 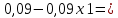 Вопрос 8. Y = 1.2x Для наших данных система уравнений имеет вид 5a + 19.375·b = 23.25 19.375·a + 133.203·b = 159.844 Домножим уравнение (1) системы на (-3.875), получим систему, которую решим методом алгебраического сложения. -19.375a -75.078 b = -90.094 19.375*a + 133.203*b = 159.844 Получаем: 58.125*b = 69.75 Откуда b = 1.2 Теперь найдем коэффициент «a» из уравнения (1): 5a + 19.375*b = 23.25 5a + 19.375*1.2 = 23.25 5a = 0 a = 0 Получаем эмпирические коэффициенты регрессии: b = 1.2, a = 0 Уравнение регрессии (эмпирическое уравнение регрессии): y = 1.2 x + 0 Эмпирические коэффициенты регрессии a и b являются лишь оценками теоретических коэффициентов βi, а само уравнение отражает лишь общую тенденцию в поведении рассматриваемых переменных. 1. Параметры уравнения регрессии. Выборочные средние. Выборочные дисперсии: Среднеквадратическое отклонение Коэффициент корреляции b можно находить по формуле, не решая систему непосредственно: a = y - b·x = 4.65 - 1.2·3.875 = 0 Линейное уравнение регрессии имеет вид y = 1.2 x + 0 |
