задачи. Массовые доли компонентов можно определить по формуле перехода
 Скачать 5.44 Mb. Скачать 5.44 Mb.
|
 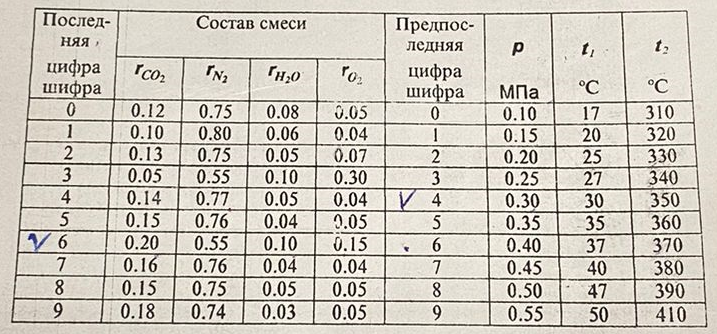
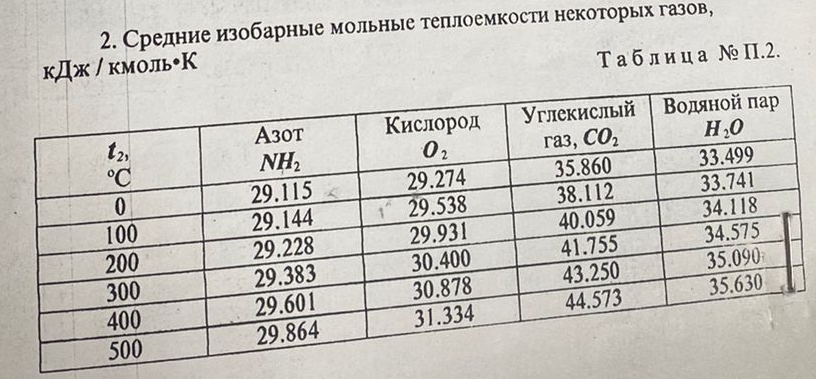
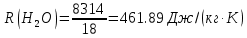 ; ;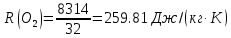 ; ;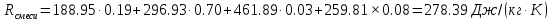 ; ;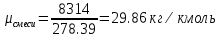 . .Плотность смеси определяют по уравнению состояния идеального газа:  ; ;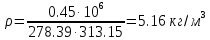 . .При физических нормальных условиях (Т=273К, Р=101325Па)  . .Из справочной таблицы выписываем средние изобарные мольные теплоемкости:
Средние изобарные мольные теплоемкости при заданных температурах находим методом интерполяции: 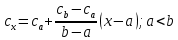 ; ;Для t1=40°C 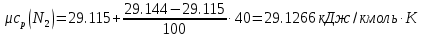 ; ; ; ; ; ; ; ;Для t2=380°C  ; ; ; ;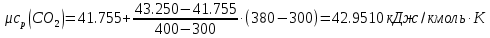 ; ;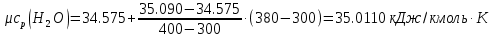 . .Средняя теплоемкость находится по формуле: 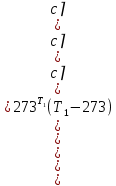 ; ;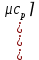 ; ;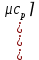 ; ;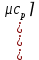 ; ;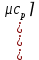 . .Мольная теплоемкость смеси находится по формуле: 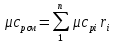 ; ;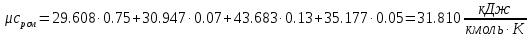 ; ;Массовую теплоемкость находим из соотношения: 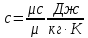 ; ; 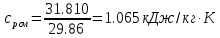 ; ;Объемная теплоемкость находится из соотношения: 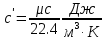 ; ;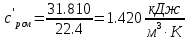 ; ;Мольную изохорную теплоемкость можно найти из уравнения: 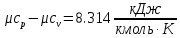 ; ;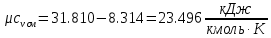 . .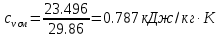 ; ;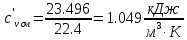 . .Количество теплоты находится по уравнению: 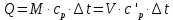 ; ;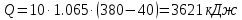 . .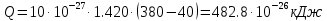 . . 
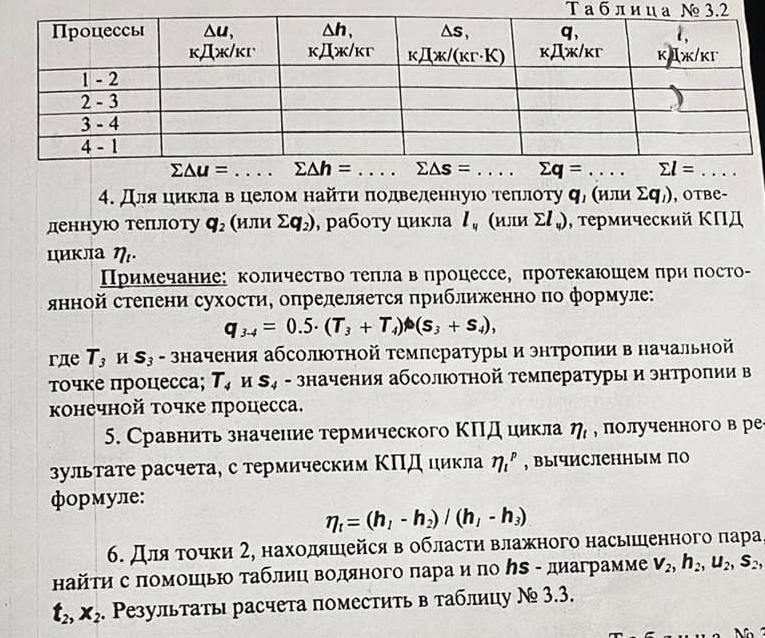
Температуру t2 определяют по формуле:  ; ; ; ;Теплоемкость политропного процесса определяется по формуле: 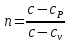 ; ; 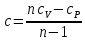 ; ;По таблице теплоемкости для многоатомного газа 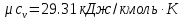 ; ;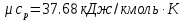 . .Связь между молярной и массовой теплоемкостью:  ; ; ; ;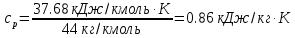 ; ;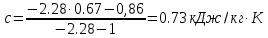 . .Для удобства дальнейших расчетов найдем показатель адиабаты k: 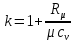 ; ; . .Работа сжатия газа: 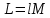 ; где ; где 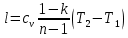 – удельная работа – удельная работа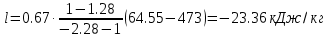 ; ;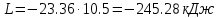 . .Общее количество теплоты, подведенное к системе, определяется по формуле:  ; где ; где  – удельное количество теплоты. – удельное количество теплоты.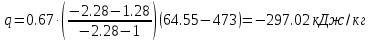 ; ;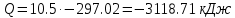 . .Изменение внутренней энергии определяют по формуле: 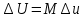 ; где ; где 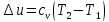 – изменение удельной внутренней энергии. – изменение удельной внутренней энергии. ; ;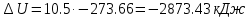 . .Изменение энтальпии определяют по формуле: 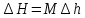 ; где ; где 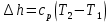 – изменение дельной энтальпии – изменение дельной энтальпии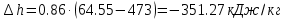 ; ; . .Изменение удельной энтропии в политропном процессе определяют по формуле: 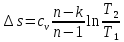 ; ;Изменение энтропии определяется по формуле:  . .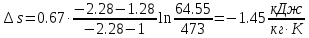 ; ; . .Адиабатный процесс – процесс без изменения энтропии. Уравнение адиабаты называют уравнением Пуассона: 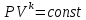 ; ;Показатель адиабаты k был вычислен ранее. k=1.28 Давление P2 можно найти через связь между параметрами состояния в адиабатном процессе: 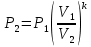 ; ;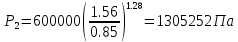 . .Температуру Т2 определяем по отношению: 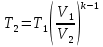 ; ;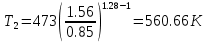 . .По первому закону термодинамики, при отсутствии теплообмена с окружающей средой работа адиабатного процесса осуществляется за счет внутренней энергии: 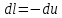 . .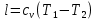 ; ; ; ;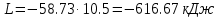 . .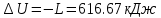 . .В адиабатном процессе ds=0, следовательно dq=ds∙T=0. ΔS=0, ΔQ=0 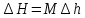 ; где ; где 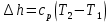 – изменение дельной энтальпии – изменение дельной энтальпии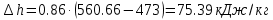 ; ;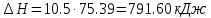 . .Изотермный процесс – процесс, проходящий при постоянной температуре. Уравнение изотермы:  . .Давление P2 можно найти через связь между параметрами состояния в изотермном процессе: 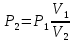 ; ;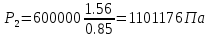 ; ;Т2=T1=473 К В случае постоянства температуры в процессе внутренняя энергия и энтальпия остаются постоянными ΔU=0; ΔH=0 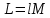 ; где ; где 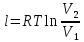 – удельная работа изотермного процесса. – удельная работа изотермного процесса. ; ; . .По первому закону термодинамики dU=dQ-dL. Т.к. dU=0, dQ=dL 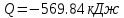 . .Изменение энтропии изотремного процесса:  ; ;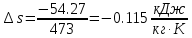 ; ; ; ;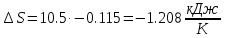 . .Сводная таблица результатов расчета:
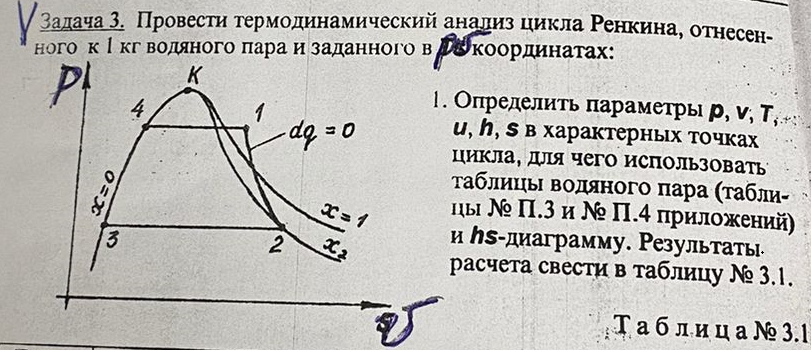 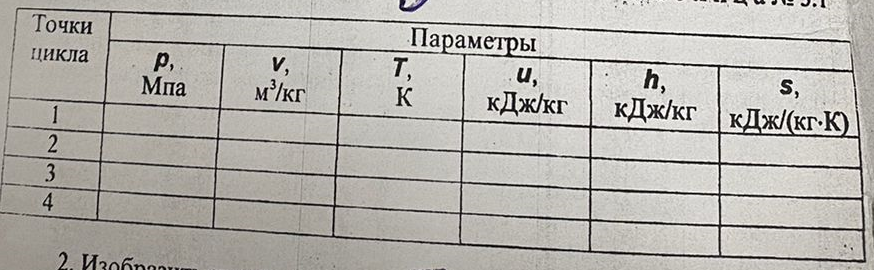             | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||

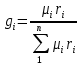 ;
;  , μi –
, μi – 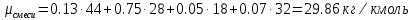 ;
; ;
;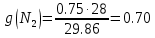 ;
;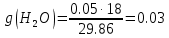 ;
;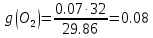 .
.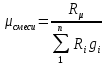 ;
; 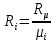 –
– 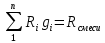
 ;
;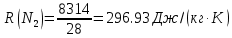 ;
;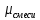 – ?
– ?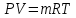 ;
;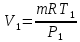 ; где
; где  – удельная газовая постоянная СО2.
– удельная газовая постоянная СО2.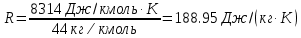 ;
;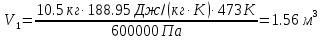 .
.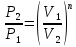 ;
; 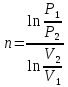 ;
; ;
;