шпоры. Вопрос 16. Визуальные методы определения места судна по пеленгам, расстояниям, пеленгам и расстояниям, горизонтальным и вертикальным углам.

• Название: Вопрос 16. Визуальные методы определения места судна по пеленгам, расстояниям, пеленгам и расстояниям, горизонтальным и вертикальным углам.
• Анкор: шпоры
• Дата: 15.06.2021
• Размер: 329.5 Kb.
• Имя файла: 16.doc
• Тип: Документы; #217393
• страница: 2 из 4

2.Если размеры и особенно ориентировка треугольника погрешно­сти в нескольких близких определениях меняются, то можно предпола­гать, что основное влияние оказывают случайные ошибки.

3.Если углы между пеленгами близки к 120° и получается равно­сторонний треугольник погрешности, то местом судна явится его центр, так как и при случайных, и при систематических ошибках ве­роятное место судна будет в этой точке.

4.При небольшом треугольнике погрешности (со сторонами менее 0,5 см) место судна можно принять в его центре, так как различные графические построения вряд ли приведут к улучше­нию результата.
Определение места судна по двум горизонтальным углам

С 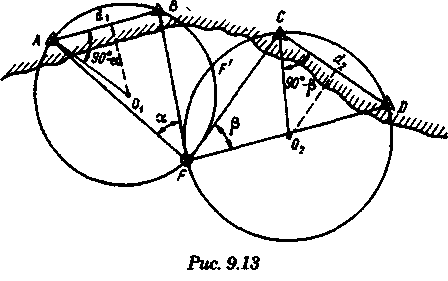пособ определения места судна по двум горизонтальным углам можно применить, когда имеется сомнение в поправке компаса или когда требуется повышенная точность обсервации, например при ве­дении дноуглубительных работ, прокладке кабеля и др.

Горизонтальный угол можно измерить секстаном или подучить как разность измеренных компасных пеленгов. На карте место судна можно получить несколькими методами: графически, с использова­нием кальки или с использованием протрактора.

Графическое решение. Если для определения места судна ис­пользованы четыре предмета (рис. 9.13), то строятся обе окружности. Чтобы найти центры и радиусы окружностей, вмещающие измеренные углы α и β при ориентирах А и В строятся углы 90° - α, при ориентирах С и D — углы 90°-β. Если углы α и β меньше 90°, то разности будут по­ложительны и углы откладывают в сторону судна. Если α и β больше 90°, то эта разность будет отрицательна и углы откладывают в сторону от судна Решение может по­лучиться двузначным, так как окружности пересекаются в двух точках. Однако на прак­тике счислимое место судна бывает известно и устранить двузначность нетрудно.

Е сли место судна опреде­ляется по трем смежным предметам, то построение упрощается
(рис. 9.14).

Пусть построена окружность, вмещающая угол α между предме­тами А и В. При точке А отложим угол β и найдем вспомогательную точку f. Соединив эту точку с предметом С, получим место в точке F, так как углы fAB + BFf = 180°, угол BFf = 180°- β, а угол BFC = β. Этот прием лучше использовать тогда, когда предмет С на­ходится далеко.

Решение с использованием кальки. Из произвольной точки О на кальке следует провести прямую Оа и относительно этой линии по­строить углы α и β (рис. 9.15). Накладывая кальку на карту и перемещая ее, нужно добиться такого положения, при котором прямые Оа, Ob, Ос проходили бы через предметы А, В, С на карте.

М 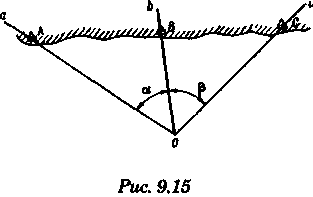есто судна отмечается уколом циркуля в точке О. Если углы не смежные, этим приемом воспользоваться нельзя.

Использование протрактора. Протрактор имеет одну непод­вижную линейку (центральную) в две подвижных.

Необходимо установить на протракторе отсчеты углов α и β a центральную линейку направить на предмет В (средний). После того как линейки протрактора совместятся с предметами А, В и С, нахо­дят место судна в центре протрактора.

Выше предполагалось, что оба угла измерены одновременно. На практике это можно сделать только при наличии двух наблюдателей. Если наблюдатель один, то измерять углы необходимо одномомент­но. Для этого сначала измеряют один угол, например α1 затем угол β и опять угол α2. Предполагая что за небольшой промежуток време­ни угол α изменяется линейно, можно принять для момента измере­ния угла β среднее значение



Показания лага и время замечают на момент измерения угла β. Этот метод имеет смысл применять только при использовании карт крупного масштаба или при производстве высокоточных обсерваций.

Обычно для уменьшения оши­бок от неодновременности изме­рений достаточно первоначаль­но измерить тот угол, смещение линии положения которого за время движения судна между наблюдениями будет наимень­шим. Если трудность измерения углов различна, то сначала лучше произвести более трудоемкое наблюдение, тогда время и отсчет ла­га должны быть отнесены к моменту второго наблюдения.

Анализ точности. Случайные ошибки в измерении горизонтальных углов секстаном равны 1...2', систематические могут быть учтены с такой же точностью. Графические ошибки при построении места судна на карте в 3...4 раза превышают ошибки наблюдений. Поскольку ошибки прокладки носят случайный характер, то при анализе точно­сти ограничимся рассмотрением лишь случайных ошибок.

Для вычисления смещений воспользуемся формулами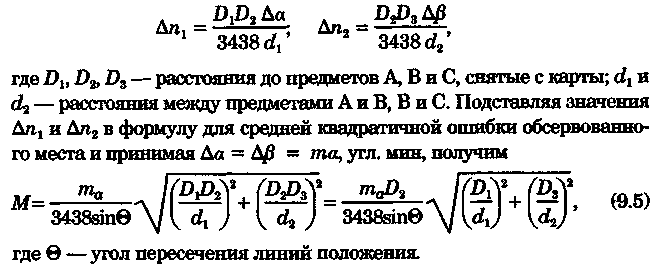







При Θ = 0° все предметы и судно будут располагаться на одной прямой. Из рис. 9.17 видно, что в какой бы точ­ке ни находилось судно (F или F'), значения углов α и β будут одинако­выми. Для избежания случая неопре­деленности надо подбирать ориентиры так, чтобы В + α + β > 180°. Это усло­вие будет соблюдаться в случаях:

а) если ориентиры располагаются на одной прямой
(рис. 9.19, а)

б) если судно находится внутри треугольника, образованного ори­ентирами (рис. 9.19, б);

в) если средний ориентир расположен ближе к судну, чем крайние (рис. 9.19, в).

П 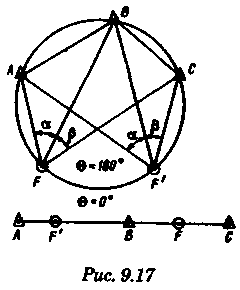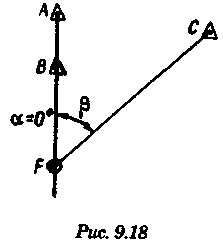редположим, что один из измеренных углов, например β равен нулю, это не влияет на решение задачи, важно, чтобы сумма В + α + β ≠ 360° или 180°. Это видно из рис. 9.18, когда место судна определяется по створу и углу.

Точность места, полученного по двум го­ризонтальным углам, в общем случае повы­шается при приближении наблюдателя к среднему предмету.

Достоинство способа в том, что он не за­висит от знания поправки компаса. Если одновременно с измерением углов взять КП одного из ориентиров, то, получив место судна по двум углам и сняв с карты ИП того же ориентира, можно рассчитать поправку компаса по формуле ∆К = ИП-КП

Н 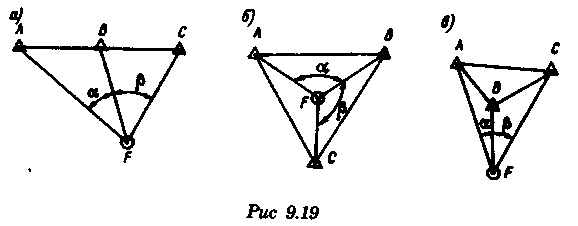едостатки способа — наличие случая неопределенности, отсут­ствие контроля и необходимость иметь в видимости, как минимум, три ориентира.

Определение расстояний в море

Расстояние в море можно определить несколькими методами: с использованием дальномеров, по вертикальному углу, измеренному секстаном, по данным РЛС и глазомерно.

Д 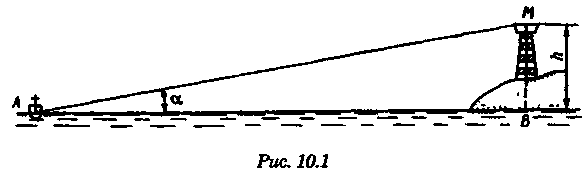альномеры представляют собой оптические приборы, измеряю­щие расстояния до видимого предмета на основе различных принципов.
Так, например, горизонтально - базисные дальномеры автомати­чески решают треугольник по известному основанию (базе прибора) и противоположному углу, измеряемому оптическим устройством.

Стереоскопические дальномеры основаны на свойстве человеческого глаза различать глубину пространства. В них решается верти­кальный прямоугольный треугольник по известной высоте предмета и измеренному противоположному углу. Точность измерения рас­стояний дальномерами зависит от базы прибора и измеряемого рас­стояния. На судах морского флота дальномеры не нашли применения и расстояния измеряются с помощью РЛС или, когда возникает необ­ходимость, с помощью секстана, позволяющего измерять угол с высо­кой точностью.

Задача определения расстояния до предмета, расположенного ближе видимого горизонта, может быть решена двумя путями — из­мерением вертикального угла между вершиной предмета и его осно­ванием или между вершиной предмета и урезом воды у береговой черты. В последнем случае в расчет вводится высота предмета над уровнем моря. В морях с приливами необходимо учитывать высоту прилива, так как высота объекта в пособиях приводятся, как прави­ло, от среднего уровня полных сизигийных вод. При измерении вер­тикального угла от основания объекта возникают затруднения, так как не всегда возможно распознать основание на фоне береговой чер­ты или строений.

При измерении вертикального угла следует различать три случая:

а) основание предмета находится ближе видимого горизонта и высота предмета известна. Тогда, измерив вертикальный угол α, можно рассчитать расстояние до предмета (рис. 10.1). Принимая уча­сток моря за плоскость, из ∆АВМ получим



Для получения D в морских милях необходимо h выразить в мор­ских милях, a tg α заменить углом, тогда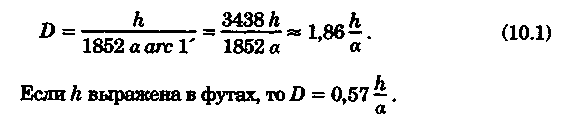



При обработке наблюдения необходимо учитывать поправку ин­декса i и инструментальную поправку s секстана, т. е.

где ос — отсчет секстана.

Земная рефракция для основания и вершины будет примерно одинаковой, поэтому ее можно не учитывать.

Формула (10.1) получена из предположения, что высота глаза равна нулю и предмет находится непосредственно у уреза воды. На практике эти условия выполняются редко, поэтому в расчетах быва­ют ошибки.

1. Ошибки из-за пренебрежения высотой глаза наблюдателя.

2. Ошибки при измерении верти­кального угла ориентира, удаленного от береговой черты на расстояние L…(в уч. Есть еще какой-то бред про точность, но я на его забил )

Определение места судна по измеренным расстояниям

Е 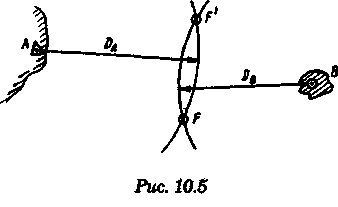сли в видимости судна имеются два ориентира, до которых измерены расстояния (по вертикальному углу или по данным РЛС), то обсервованное место судна можно получить по двум расстояниям. Пусть А и В—два объекта, до которых измерены расстояния DA и DB. Известно, что изме­ренному расстоянию соответствует изолиния — окружность радиусом, равным этому расстоянию, и с центром в точке расположения ориентиров. Если оба наблюдения сделаны одновременно, то, проложив две окружно­сти, в одной из точек получим место судна (рис. 10.5). Вопрос о том, какую из двух точек считать обсервованным местом, легко решается путем со­поставления со счислимым местом.

Ошибки в определении места судна по двум расстояниям зависят от трех факторов:

• 
  н 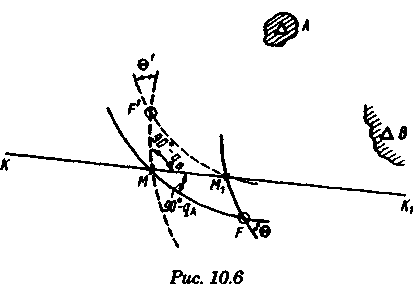еодновременности измерения расстояний,
  
• 
  ошибок измерений
  
• 
  и угла пересечения линий положения.
  

Чтобы уменьшить влияние неодновременности измерения расстояний, нужно первым измерять расстояние до предмета, который находится ближе к тра­верзу, так как смещение линии положения из-за движения судна в этом случае будет меньше (рис. 10.6).

Пусть А и В — два ориентира, по которым определяется место суд­на. Бели первым, когда судно находится в точке М, измерить расстоя­ние до ориентира А, вторым, когда судно находится в точке М1 — до ориентира В, то получим место в точке F. При обратном порядке изме­рения расстояний место судна получается в точке F'. Поскольку всегда целесообразно определять место судна в момент последних наблюде­ний, сравним отрезки FM1 иF'M1.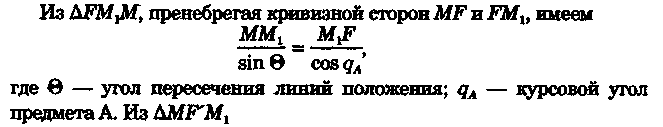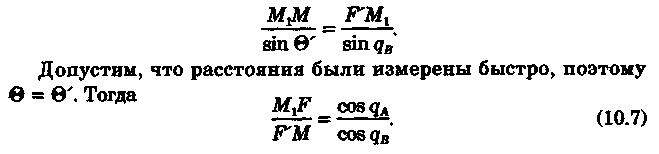





Из равенства (10.7) видно, что для уменьшения ошибки, вызван­ной неодновременным измерением расстояний, первое наблюдение нужно делать до ориентира, расположенного ближе к траверзу.

Для исключения ошибки от неодновременности измерения рас­стояний можно произвести осреднение первого наблюдения, если его повторить после второго.

Если между измерениями расстояний промежуток времени со­ставляет несколько минут, то выполняется графическое приведение линий положения к одному моменту. Для этого вторая линия поло­жения смещается по курсу на величину пройденного расстояния, за данный промежуток времени.

Средняя квадратичная погрешность обсервованного места по двум расстояниям получается, если в общую формулу (8.12) подста­вить значения ошибок линий положения, помня, что градиент рас­стояния равен единице: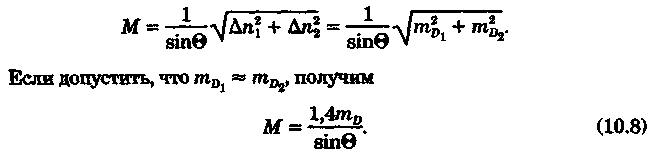



Определение места судна по крюйс-пеленгу

Е 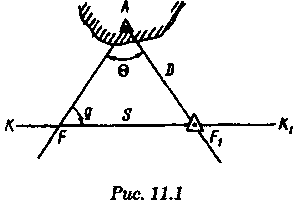сли в видимости судна имеется только один ориентир, который можно использовать для взятия пеленга, наблюдатель, находящийся на стоящем судне, получит одну линию положения. Место в этом слу­чае определить нельзя. Положение меняется, если наблюдатель нахо­дится на движущемся судне и элементы движения известны.

Обозначим через КК1 линию пути судна (рис. 11.1). Когда судно находилось в точке F, был взят первый пеленг ориентира А. Через некоторое время из точки F1 взят второй пеленг того же ориентира. Если путь судна и пройденное расстояние известны, то, вычислив угол Θ — разность пеленгов и угол q — курсовой угол предмета А в момент первого измерения пеленга, можно рассчитать D — расстоя­ние до предмета А в момент второго измерения пеленга. Из ∆FAF1



При определении по крюйс-пеленгу место судна будет в точке пе­ресечения двух линий положения: второго пеленга и окружности ра­диусом D с центром в точке А. Так как вторая линия положения по­лучается через элементы счисления (S и q), то место, найденное этим методом, называется счислимо-обсервованным.

На практике для нахождения места судна вместо расчетов D, пользуются графическим решением
(рис. 11.2).

По линии пути судна KK1 или по линии пути К1 проложенной на карте от предмета А, откладывают от точки пересечения с линией пер­вого пеленга n пройденное судном расстояние S за время между пе­ленгами и из полученной точки m прокладывают прямую, параллель­ную первому пеленгу, до пересечен 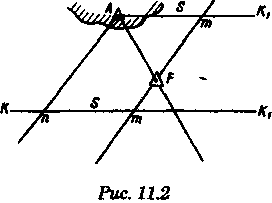ия со вторым. Это будет приведен­ная линия положения; в точке пере­сечения этой линии со вторым пелен­гом будет место судна (точка F на рис. 11.2). Определение места судна по крюйс-пеленгу может быть еще истолковано как перенос первой ли­нии положения по счислению парал­лельно самой себе к моменту получе­ния второй линии положения.

Е сли нет дрейфа и течения, пройденное судном расстояние по показаниям лага, исправленное его поправкой, откладывают на линии ИК, а при дрейфе — на линии пути судна Причем для лагов, жестко скрепленных с корпусом судна, необходимо откладывать не просто SЛ, a SлSecα (α — угол дрейфа).

При наличии течения, когда элементы его известны, плавание суд­на между пеленгами нужно проложить с учетом действующего тече­ния. Для этого
(рис. 11.3) из произвольной точки n на первом пеленге прокладываем линию ИК судна и плавание его по лагу за время между пеленгованиями. Из полученной точки m прокладываем отрезок, рав­ный сносу от течения за тот же промежуток времени mf = vtt, и через точку f проводим прямую, паралельную первому пеленгу.

При аналитическом учете течения на линии пути необходимо от­ложить расстояние, пройденное судном относительно грунта:



Если за время определений судно меняло курс, то между пеленга­ми необходимо отложить все отрезки ИК и SЛ (рис. 11.4).

Способ крюйс-пеленга можно использо­вать и для определения места судна по раз­новременным пеленгам двух предметов, причем решение в этом случае существенных отличий не имеет.

Рассматривая способ крюйс-пеленга как определение места судна по двум линиям по­ложения (первой приведенной и второй ли­нией положения), напишем формулу для средней квадратичной ошибки обсервованного места



где mл1, mл2 — средние квадратичные ошибки первой и второй линий положения; mр — средняя квадратичная ошибка при­веденной линии положения, обусловленная ошибками в направлении и величине пе­ремещения судна, средние квадратичные ошибки которых равны mк и ms