ВЫЧИСЛИТЕЛЬНАЯ ТЕХНИКА экз. Вопрос. Структурная схема и принцип работы арифметико логического устройства (алу)
 Скачать 147.78 Kb. Скачать 147.78 Kb.
|
|
Билет №4. Вопрос. Структурная схема и принцип работы арифметико – логического устройства (АЛУ). Арифметико-логическое устройство (АЛУ) предназначено для выполнения всех арифметических и логических операций над числовой и символьной информацией (в некоторых моделях ПК для ускорения выполнения операций к АЛУ подключается дополнительный математический сопроцессор); Принцип работы арифметико–логического устройства будет ниже рассмотрен на примере простого АЛУ, работающего с двумя четырехразрядными операндами. 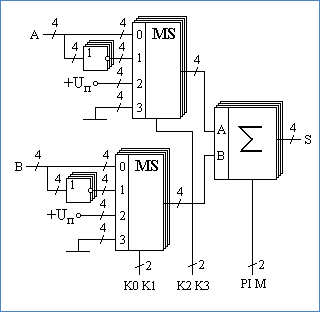 Рисунок 1 – Структурная схема упрощенного АЛУ. На рис.1 приведена упрощенная схема арифметико-логического устройства. В данной схеме используются четырех-входовые коммутаторы, для управления каждым из которых достаточно двух бит. То есть для управления всей схемой в целом достаточно четырёх проводов управления. В зависимости от значений управляющих сигналов K0, K1, K2, K3 устройство будет совершать различные математические операции над входными значениями операндов A и В. В зависимости от значений управляющих сигналов, поданных на каждый коммутатор, сумматору будет передан либо непосредственно сам операнд, либо его инверсия, либо последовательность нулей или единиц. На результат операции будет влиять вход переноса сумматора PI, поэтому этот провод тоже включим в состав кода, управляющего схемой АЛУ. Операции, которые выполняются арифметической схемой в зависимости от поданного на управляющие линии кода, приведены в таблице 1. Проанализируем эту таблицу. Если на все управляющие входы подать низкий потенциал, то к входу сумматора будут подключены коды A и B без инверсии. В этом случае будет производиться операция суммирования. Эта ситуация отображена первыми двумя строками таблицы выполняемых операций. Операция вычитания осуществляется второй, третьей, восьмой и девятой строкой. В этом случае один из операндов поступает на вход сумматора через блок инверторов. Правда для получения дополнительного кода не хватает единицы, но её можно подать на вход переноса сумматора PI. Ещё одной часто используемой операцией является увеличение числа на единицу или уменьшение числа на единицу. Эти операции позволяют легко организовывать циклы в программе и переходить от предыдущего операнда к следующему. Такие операции могут быть выполнены при помощи кодов, записанных в строках четыре, семь, шестнадцать и двадцать пять. Кроме того, схема арифметического устройства может просто передавать на выход любой из входных кодов без изменения, что позволяет осуществлять копирование данных (суммирование с константой ноль) через это устройство без дополнительных схем коммутации. Таблица 1 – Операции, выполняемые арифметической схемой в зависимости от поданного на управляющие линии кода. 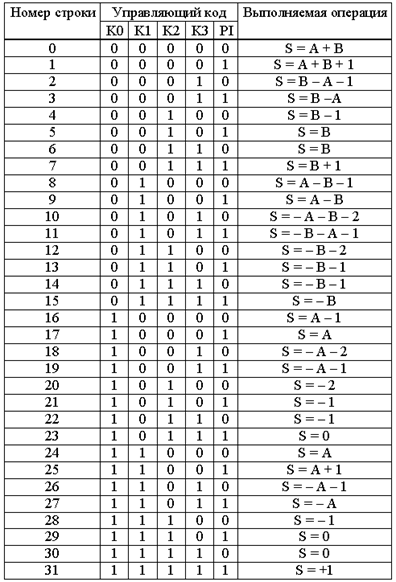 Арифметические операции Операции, выполняемые арифметико-логическим устройством АЛУ может выполнять следующие арифметические операции: 1) Изменение знака – neg (negation) 2) Нахождение абсолютного значения – abs (absolute) 3) Сложение – add (addition) 4) Вычитание – sub (substruction) 5) Сравнение – cmp (comparision) Примеры: Изменение знака neg  Вычитание  АЛУ может выполнять следующие специальные операции: 1) Округление – round(roundong) нескольких типов – банковское, сигнальное, и др. 2) Насыщение – sat (saturation) 3) Вычитание и сложение – subadd 4) Сложение и вычитание – addsub Примеры: Сложение и вычитание  Насыщение sat 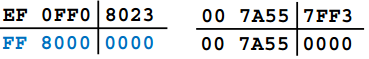 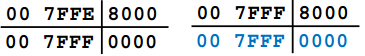 Округление round 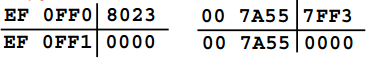 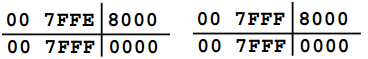 Разница между банковским и сигнальным округлением 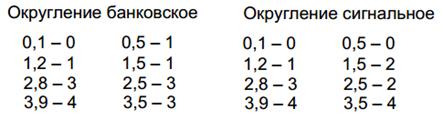 Логические операции АЛУ может выполнять следующие логические операции: 1) Конъюнкция – and 2) Дизъюнкция – or 3) Неэквиваленция – xor (exclusion or) 4) Отрицание – not 5) Пересылка – nop (no operation) 6) И другие Примеры: Конъюнкция and  Неэквиваленция xor 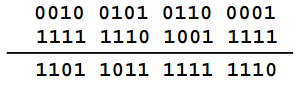 АЛУ может выполнять следующие битовые операции: 1) Проверка бит – btst (bit test) 2) Установка бит – bset (bit set) 3) Установка бит с проверкой btstset (bit test and set) 4) Очистка бит – bclr (bit clear) 5) Очистка бит с проверкой btstclr (bit test and clear) 6) Инверсия бит – bnot (bit complement) Примеры выполнения битовых операций: 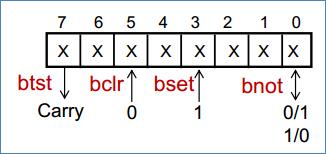 Рисунок 2 – Примеры выполнения битовых операций Задача. Найти значение логического выражения: (a а) a = 5, z = – 4; первое условие: a второе условие z>2: -4>2 – ложь третье условие a=5: 5=5 правда так как между выражениями стоит логическое «или» то выражение правдиво б) a = –5, z = 0. первое условие: a второе условие z>2: 0>2 – ложь третье условие a=5: --5=5 ложь так как между выражениями стоит логическое «или» то выражение правдиво Ответ: таблица истинности для двух пунктов
|
