Компьютерная графика контрольная. Вопросы для экзамена по курсу. Вопросы для экзамена по курсу "Компьютерная графика"
 Скачать 278.18 Kb.
|
 Каждая из этих утилит позволяет настроиться на большой перечень устройств соответствующего класса. При этом выполняется преобразование нормированных координат файла *.PLT в координаты устройства По тому же принципу работает Windows95 при формировании заданий на печать. Если памяти достаточно, сначала формируется файл печати в формате расширенного метафайла (EMF). Метафайл формируется быстрее, т.к. не зависит от типа устройства. Далее в фоновом режиме формируется задание на печать с учетом конкретного устройства.Отображение области действия мировых координат в область действия координат устройства называется ФУНКЦИЕЙ КАДРИРОВАНИЯ. Изображение, получаемое средствами машинной графики, имеет четко определенную структуру. Атомарным (неделимым) объектом является КООРДИНАТНАЯ ТОЧКА или ПИКСЕЛ. Термин ПИКСЕЛ, введенный для дисплеев, нашел применение в более широком смысле. Это точка, являющаяся атомарным компонентом изображения вне зависимости от того, где и как хранится/отображается рисунок. 6. Понятие графического примитива. Наиболее распространенные графические примитивы и операции над ними. ГРАФИЧЕСКИЙ ПРИМИТИВпредставляет собой либо координатную точку, либо упорядоченную последовательность (не совокупность, а именно последовательность!) координатных точек. Различают графические объекты (и соответственно графические примитивы): нульмерные (точки), одномерные (линии), двумерные (поверхности), трехмерные (тела). В компьютерной графике все, что относится к двумерным изображениям, обозначают 2D (2-dimension), к трехмерным - 3D (3-dimension). 7. Основные отличия текстового и графического режима видеоадаптера. Любой современный видеоадаптер может работать в двух режимах: текстовом и графическом. В текстовом режиме экран делится на ячейки, соответствующие размеру символа. Обычно это 40 или 80 колонок, 25 или 50 строк. Каждая ячейка содержит атрибут и символ. Символ выводится на экран в ASCII коде, атрибут указывает, как представляется символ на экране (цвет, интенсивность, мерцание, подчеркивание, инверсное изображение в зависимости от типа видеоадаптера). Язык программирования С и другие языки такого же класса имеют средства управления выводом текста, в том числе управления атрибутами символов. В графическом режиме экран представляется совокупностью пикселов. Количество точек (разрешающая способность) зависит от типа видеоадаптера и установленного для него режима. В текстовом режиме верхний левый угол экрана имеет позицию (1,1), координата Х растет вправо, координата Y растет вниз. В графическом режиме верхний левый угол имеет координаты (0,0), координаты Х и Y направлены аналогично. 8. Чем отличаются с точки зрения машинной графики видеоадаптеры EGA,VGA,SVGA,MGA. Режим обозначается номером и определяется разрешением экрана и количеством цветов.
Каждая видеоплата содержит собственный BIOS для работы с ней и поддержки основных своих функций. Через BIOS можно определить тип адаптера - EGA или VGA, установить нужный режим, системный шрифт заданного размера (8,14 или 16 пикселов высоты), палитру. Для 16-цветных режимов под каждый пиксел отводится 4 бита (24=16). Однако эти биты располагаются не последовательно в одном байте, а разнесены по 4 блокам (битовым или цветовым плоскостям) видеопамяти. Вся видеопамять (обычно 256 К) делится на 4 равные части. Каждому пикселу соответствует по 1 биту каждой плоскости, причем эти биты расположены одинаково относительно начала плоскости (параллельно). Когда процессор выполняя операции чтения/записи видеобуфера по некоторому адресу, этот адрес относится не к одному, а к 4 байтам, каждый из которых размещается в своей битовой плоскости. При выполнении операции чтения из видеобуфера (например, командами MOV reg,mem; LODS; CMP reg.mem и др.) из него извлекается не 1, а 4 байта. Но данные пересылаются не в процессор, а в четыре 8-битовых регистра-защелки (latch - задвижка, щеколда). Каждый из этих регистров соответствует своей битовой плоскости. При выполнении операций записи в видеопамять производится параллельная модификация всех 4 битовых плоскостей. Таким образом за один раз обрабатывается информация о 8 пикселах. Если к видеобуферу обратиться при помощи команд, оперирующих словами, а не байтами, результаты могут быть ошибочными, т.к. алгоритм выполнения операций процессора и видеокарты разный, и результат одной части операции перезаписывается другой ее частью.  Регистры видеокарты делятся на группы. Каждой группе соответствует пара последовательных портов (порт адреса и порт значения). Для записи в регистр значения надо записать сначала номер регистра в порт адреса, затем значение в следующий порт. Добраться до регистров видеокарты можно с помощью ассемблера или функций языка С inportb, outportb (запись в аппаратный порт). Прототипы функций - в Передачей данных между процессором, регистрами-защелками и видеобуфером управляет графический контроллер. В адаптере EGA это 2 микросхемы или отдельная СБИС, в адаптере VGA он входит в СБИС видеографической матрицы. Графический контроллер имеет 9 регистров, адресуемых через порт 3CEh. Значения регистров задаются через порт 3CF. Содержимое регистров графического контроллера управляет обработкой данных регистров-защелок при чтении/записи. Часть операций в качестве операндов используют байт, т.е. воздействуют отдельно на каждый регистр. Операндом других операций является пиксел, т.е. содержимое регистров-защелок рассматривается как набор из 8 пикселов. Такие операции воздействуют на каждый пиксел в отдельности. Т.к. разрядность процессора не более 32, требуется специальное формирование значения для пересылка в процессор. Оно осуществляется с помощью масок и зависит от режима чтения/записи. Режим задается в специальном регистре графического контроллера. Этот регистр имеет номер 5. Имеется 2 режима чтения и 3 режима записи для EGA. Для VGA имеется еще один режим записи. Бит 3 регистра определяет режим чтения (0 или 1), биты 1 и 0 - режим записи Остальные биты этого регистра обычно нулевые. В режиме чтения 0 в процессор передается значение одного из 4 регистров-защелок. Указателем номера регистра-защелки служит специальный регистр считываемого банка (еще одно название битовой плоскости) Этот регистр имеет номер 4. Такое последовательное чтение битовых плоскостей применяется, например, npi записи изображения на диск. В режиме чтения 1 задействованы 2 регистра видеокарты, управляющие цветами. Этот режим позволяет быстро находить пикселы, имеющие заданный цвет (требуется, например, при закрашивании, при разделении фоновых и нефоновых пикселов). Однако гарантированно быстро узнать цвет конкретного пиксела нельзя. Максимально для этого может потребоваться 16 раз считывание (по количеству цветов). Режим записи 0 является наиболее сложным, но дает большие возможности. Операция записи процессора инициирует комбинацию байтных и пиксельных операций. Байт данных от процессора можно использовать для модификации содержимого любых или всех битовых плоскостей и одновременно некоторое заданное значение пиксела можно использовать для модификации всех или любых пикселов. Значение пиксела - еп цвет. В операции задействованы 4 служебных регистра графического адаптера, вместе с байтом данных от процессора воздействующих на регистры-защелки. Например, регистр битовой маски (номер 8) позволяет выделить нужный пиксел, чтобы сопоставить ему определенный цвет. Регистр маски плоскости (относится к группе регистров, адресуемых через порт ЗС4. порт данных - ЗС5) защищает от изменения определенные плоскости. Для формирования значений используются также сдвиговые операции. В режиме записи 1 значения регистров-защелок непосредственно копируются в соответствующие бито вые плоскости. Другие регистры не действуют, посланное процессором значение не учитывается. Этот режим позволяет быстро копировать содержимое видеопамяти группами по 8 пикселов. Очевидно, режим может действовать только после заполнения регистров-защелок, когда процессор прочитает данные из видеобуфера Обычно этот режим применяется при перемещении изображения из одной области экрана в другую. В режиме записи 2 младшие 4 бита байта, посланного процессором, задают цвет отображения не защищенных битовой маской пикселов. Как уже отмечалось, регистр битовой маски защищает от изменения определенные плоскости. Регистр 3 графического контроллера устанавливает способ наложения новых пикселе на существующее изображение, т.е. логическую операцию, применяемую к регистрам-защелкам и значении посланному процессором. Этот режим удобен для записи в видеобуфер (на экран) отдельных пикселов. Режим записи 3 поддерживается только адаптером VGA. В [3,4] излагается способ формирования данных для записи в битовые плоскости. Работа VGA в 256-цветном режиме с разрешением 320*200 имеет особенности. Для одновременного отображения такого количества цветов под каждый пиксел отводится 8 бит. Эти биты идут последовательно образуя 1 байт. Плоскости не используются, видеопамять начинается с адреса 0хА000:0. Точке с координатам (х,у) соответствует байт памяти по адресу 320*у+х. Это стандартный режим с номером (mode) 13. Существуют также нестандартные режимы адаптера VGA при работе с 256 цветами. Они программируются на ассемблере и позволяют установить повышенное разрешение (320*240 или 360*480). Здесь используются битовые плоскости, в которых в определенном порядке хранятся пикселы. В одной битовой плоскости хранятся пикселы 0,4,8 и т.д., в другой - 1,5,9 и т.д. Здесь также задействованы все служебные регистры, н меняется интерпретация находящихся в видеопамяти значений. Видеокарты SVGA совместимы с VGA, но имеют большой набор дополнительных режимов. VGA является стандартом, SVGA - его расширение. В 256-цветном режиме в адаптерах SVGA под каждый пиксел отводится 1 байт, вся видеопамять разбивается на банки одинакового размера (обычно по 64 К). Область адресного пространства 0хА000:0 -0xA000:0xFFF соответствует выбранному банку. Ряд карт позволяет работать сразу с двумя банками. Практически все различия между картами заключаются в установке режима с заданным разрешением и установке банка с заданным номером. Можно построить библиотеку, распознающую наличие основных SVGA карт (Triedent, Cirrus Logic и др.) и обеспечивающую работу с ними. Связь - через порты 0хЗС4 и 0хЗСЕ, работать можно на Си с привлечением ассемблера. Ассоциацией стандартов в области видеоэлектроники VESA (Video Electronic Standards Association сделана попытка стандартизации работы с различными SVGA-платами путем добавления в BIOS платы (у видеоадаптеров - свой BIOS) некоторого стандартного набора функций, обеспечивающего получение необходимой информации о карте, установку заданного режима и банка памяти. При этом вводится стандартный набор расширенных режимов. Номер режима - 16-битовое число, биты с 9 по 15 зарезервированы и должны быт; равны 0, бит 8 для VESA-режимов = 1, для «родных» режимов карты = 0. Таблица основных VESA-режимов:
Ряд SVGA-карт поддерживает т.н. непалитровые режимы. Здесь для каждого пиксела вместо индекса в палитре непосредственно задается его RGB-значение. Обычно такими режимами являются HiColor (15 или К бит на пиксел) и TrueColor (24 бита на пиксел). Видеопамять, этих режимов устроена аналогично 256-цветны» SVGA: под каждый пиксел отводится 2 байта для HiColor и 3 байта для TrueColor, байты расположены подряд и сгруппированы в банки. Наиболее проста организация TrueColor (16 млн. цветов) -1 байт под каждую из компонент цвета. Для HiColor под каждый пиксел отводится 2 байта. Здесь возможны варианты: • каждая компонента занимает по 5 бит, последний бит не используется. Это дает всего 32 тысячи цветов; • красная и синяя компоненты занимают по 5 бит, зеленая - 6 бит. Это дает всего 64 тысячи цветов. 9. Особенности представления цвета в видеоадаптерах EGA и VGA. Известно, что любой цвет является композицией трех основных цветов: Red (красный). Green (зеленый), Blue (синий). Дополнительные цвета - смесь основных: При различной аппаратной настройке монитора magenta, например, может быть пурпурным, сиреневым, малиновым, вишневым; голубой - бирюзовым. В зависимости от интенсивности (яркости) каждого из основных цветов в смеси получаем различные оттенки Следовательно, 4-битовая комбинация позволяет закодировать 15 базовых цветов. Кодирование стандартно: 1 - интенсивность, RGB - цвета. Т.к. емкость видеопамяти ограничена, в ряде случаев возникает конфликт между цветностью и разрешающей способностью. Этим объясняется возможность цветных видеоадаптеров работать в разных режимах (модах), позволяющих увеличивать разрешающую способность (количество точек) за счет уменьшения количества цветов и наоборот. (См. параметр graphmode функции initgraph()) Например, в простейшем случае для адаптера CGA возможны 2 варианта представления изображений: 2 бита на каждый пиксел (4 цвета, 320*200 точек) и 1 бит на каждый пиксел (2 цвета, 640*200 точек). Для VGA можно получить 640*200 точек при воспроизведении 16 цветов из палитры 4096 оттенков или 320*200 точек при воспроизведении одновременно 256 цветов. Т.к. видеопамять VGA 256 К, можно также уменьшить число страниц видеобуфера (вместо 2 получить 1, 16 цветов, 640х480 точек). Практически любой видеоадаптер способен отобразить гораздо больше цветов, чем определяется коли чеством бит, отведенным под один пиксел. Например, монитор EGA адаптера способен отображать 64 цвета т.к. имеет 6-битовый видеосигнал. Видеоадаптер переводит 4-битовый цвет пиксела в 6-битовый видеосигнал Для перевода используется некоторое подобие таблицы, называемое палитрой. Фактически адаптер имеет К специальных внутренних регистров, где для каждого логического цвета хранится его 6-битовое значение видеосигнала (6 бит, т.к. 3 основных цвета + бит интенсивности, следовательно, на каждый цвет - 2 бита). Цвет в палитре задается байтом вида 00rgbRGB. Малые буквы обозначают бит интенсивности соответствующего цвета, Существует возможность менять в таблице соответствие логического цвета и видеосигнала, выбирая его из 64 возможных цветов. (4-битовый атрибут) & (Регистр используемой цветовой матрицы) = Регистр палитры 0-0F h = 6-битовый сигнал, подаваемый на дисплей. Реализация 16-цветной палитры для VGA гораздо сложнее. Для каждого цвета имеется 18-битовая раскладка по компонентам (6 бит на каждый из 3 основных цветов - в EGA было по 2 бита на цвет). Дополнительные биты дают более тонкую раскладку по интенсивности, т.е. обеспечивают более разнообразное смешивание 3 основных цветов. Схема получения 18-битового сигнала на начальном этапе повторяет EGA, далее задействован еще ряд регистров, операции логического И. . Помимо поддержки EGA видеоадаптер VGA имеет 256 специальных регистров, где для каждого цвета хранится его 18-битное представление. Обычно BIOS записывает в эти регистры набор цветов, принимаемый по умолчанию. Этот режим используется для получения 256 цветов при разрешении 320*200. Распределение цветов по регистрам видеоадаптера VGA:
Регистры 0h - 0Fh (h - hex, 16-ричный) обеспечивают CGA-совместимый набор цветов, принимаемый по умолчанию. Регистры 10h - 1Fh содержат упорядоченный по возрастанию набор оттенков серого. Следующие 216 регистров (20h - F7h) содержат 3 группы по 72 цвета, где первая группа (20h - 67h) -цвета повышенной яркости, вторая группа (68h - AFh) - средней, третья (BOh - F71i) - пониженной. Каждая такая группа состоит из трех диапазонов цветов, упорядоченных по снижению яркости. Снижение яркости можно трактовать как увеличение количества белого цвета, подмешанного к основному. Цвета в каждом диапазоне располагаются в порядке перехода от синего через красный к зеленому. При 16-цветной работе VGA исходному логическому номеру цвета для 6-битовой палитры EGA сопоставляется, как и ранее, значение от 0 до 63. Но это уже не RGB-разложение цвета, а номер одного из 256 регистров, содержащих физический цвет. Для установки значений регистров служит функция void far setrgbpalette(int color, int red, int green, int blue); color - логический номер цвета (от 0 до 15 или от 0 до 255 в зависимости от graphmode), остальное - его RGB-интенсивности (используются только младшие байты, только 6 битов каждого байта). Функция setpalette() присваивает одному из 16 логических цветов значение физического цвета из диапазона 0 - 63. Функция setrgbpalette() делает то же самое, но диапазон цветов шире 10. Как программно осуществляется управление принтером. Принтеры очень хорошо приспособлены для вывода графики, т.к. строят изображение по точкам. Принтером управляет специальный набор команд, описываемый в документации на принтер. Эти команды отражают аппаратные особенности принтера. Однако есть достаточно общий набор команд, реализованный для большинства принтеров Это команды управления прогоном бумаги, плотностью печати, шрифтом (если принтер имеет возможность работы с различными шрифтами - зашиваются в ПЗУ) и т.д. Каждая команда является набором символов (имеет символическое имя) или цифр (кодов). Коды просто посылаются на принтер во входном потоке. Чтобы отличить команды от того, что следует напечатать, они предваряются неотображаемым символом, т.е. символом с кодом, меньшим 32. Такому коду не соответствует ни один символ кода ASCII. Обычно в качестве символа начала управляющей последовательности выступает Esc (код 27). Поэтому говорят об Esc-последовательностях управления принтером. При работе на языке С Esc-последовательности записываются в операторе вывода. Символ Esc выглядит как ‘\х1В’. Послать его можно в любой функции вывода, переключив поток вывода с экрана на принтер, или непосредственно в принтерный порт с помощью функции int biosprint(int cmd, int byte, int port); где cmd: 0 - печать символа byte, 1 - инициализация порта принтера, 2 - чтение статуса принтера; byte - от 0 до 255 (что выводим/посылаем на принтер). port - определение принтерного порта: 0 - LPT1; 1-LPT2 и intbyte='\xlB'; biosprint(0,byte,0); 24-игольчатые (или LQ) принтеры включают (расширяют) язык управления 9-игольчатых принтеров. Большинство струйных принтеров по языку управления совместимо с LQ-принтерами. Среди лазерных принтеров наиболее распространены HP LaserJet фирмы Hewlett Packard. Они управляются языком PCL. Большинство лазерных принтеров других фирм тоже поддерживает этот язык. Для выделения управляющей информации также используются Esc-последовательности, но кодовая строка длиннее, т.к. эти принтеры предоставляют больше возможностей по управлению. 11. Основные отличия в подходах MS DOS и WINDOWS при разработке графических приложений. Операционная система Windows выводит графику посредством интерфейса графических устройств GDI - Graphic Device Interface. Текст тоже рассматривается как графика. GDI обеспечивает вывод на экран, принтер, плоттер и др. GDI избавляет приложения Windows от необходимости учитывать многие особенности устройств вывода. Например, как мы уже видели в DOS, адресация видеопамяти адаптеров CGA, EGA, VGA, SVGA выполняется по-разному. К тому же представление видеоданных сильно зависит от видеорежима (разное количество байт на пиксел в зависимости от mode). Однако приложения Windows не работают непосредственно с видеопамятью. Вызываются соответствующие функции GDI реализованного в виде DLL. Функции GDI также не работают с аппаратурой. Для выполнения нужной графической операции GDI вызывает драйвер устройства вывода, ориентированный на особенности аппаратуры. Таким образом; GDI позволяет организовать вывод на некоторое логическое устройство. Функции GDI и драйверы обеспечивают независимость приложений от аппаратуры. Это многие рассматривают как преимущество перед MS DOS, т.к. в MS DOS для повышения производительности приходится работать непосредственно с регистрами видеоконтроллера и видеопамятью (как это рассматривалось выше). С другой стороны, недоступность операций низкого уровня не позволяет нам влиять на производительность и отдает решение этих вопросов только на откуп создателей соответствующих системных программных средств. Логические устройства дают программисту большую свободу выбора выразительных средств. Например, логический видеомонитор имеет огромное разрешение, способность отображать практически любой цвет (Реально - до 16 млн. цветов). Если задан цвет для палитры в 16 млн. цветов, а устройство не имеет такой возможности, GDI выбирает наиболее близкий к требуемому цвет. Для монохрома - градации серого. Ситуация, когда приложение запрашивает у Windows одно, а получает другое, возникает и при работе со шрифтами. Это повышает независимость от аппаратуры по сравнению с MS DOS. В MS DOS при работе с видеоадаптерами указываются конкретные цвета, из файлов загружаются конкретные шрифты Для новых устройств в программу вносятся изменения (хотя бы в связи с новыми именами файлов). Следовательно, программы MS DOS более аппаратно зависимы. Приложения Windows не меняются при смене аппаратуры, требуется только соответствующий драйвер. Чем лучше аппаратура, тем ближе цвет и шрифт будут к запрошенным. Таким образом, в MS DOS можно запросить только то, что имеется, в WINDOWS предложен другой подход к разработке приложений: запрашивай максимум того, что надо.  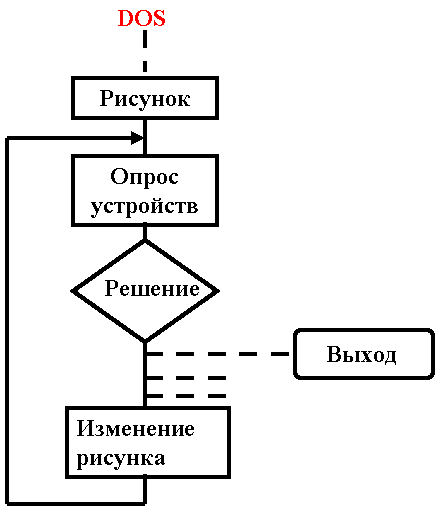  12. Основные этапы преобразования и модели, используемые при переходе от изображений реального мира к компьютерным. Для описания графической информации используется иерархическая совокупность математических моделей. В зависимости от формы представления существует 4 основных модели графических изображений: Ми (М0) - исходное (непрерывное) изображение; Мр (M1) - растровая модель (изображение); Мв (M2) - векторная модель (изображение); Мп (МЗ) - прикладная модель (описание изображения в терминах хранения). Технология преобразования графических представлений - отображение Q: Ми—Мп. Технологический процесс - отображение Pi, осуществляющее получение i модели по (i-1)-ой: Pi: M(i-l) — Mi Технологическая операция (этап) - отображение T(iJ). внутри осуществляющее преобразование одной модели: TiJ: M(ij-l) —^ MiJ Укрупненно технология преобразования изображения из начальной модели в конечную:
13. Основные этапы растр-векторного преобразования графических объектов. Процесс сканирования зависит от принципов работы сканера. Поэтому его не рассматриваем. Наиболее объемным и важным является второй этап, называемый также оцифровкой изображения. Бинарные изображения более просты. По сравнению с полутоновыми изображениями они имеют ограниченный класс шумов. Основной метод подавления шумов - логическая фильтрация. Наиболее часто встречающийся вид искажений графических изображений - неоднородность формы линий. Это может выражаться в • изменении толщины (наличии слишком широких или узких участков линий); • наличии изолированных черных пятен небольших размеров или изолированных пустот внутри линий; • разрывах линий, слиянии нескольких линий (встречается редко, устранение трудоемко). Основным фильтром, используемым для подавления шумов бинарных изображений, является сглаживающий фильтр, изменяющий значение центрального элемента окрестности в зависимости от количества однотипных с ним элементов в заданной окрестности. Алгоритм последовательного просмотра растра и применения каждому элементу данного фильтра называется алгоритмом логического сглаживания. Выделение средних линий (скелетизация) позволяет описать геометрические особенности объекта, что удобно при последующей обработке. Существует два типа алгоритмов выделения средней линии. 1. Утоньшение, которое можно рассматривать как итерационное преобразование множества, имеющего непустую внутренность, в множество единичной ширины поперечного сечения путем последовательного его сжатия с обеих сторон. 2. Выделение скелета или средних осей объекта, т.е. выделение всех точек, равноудаленных по меньшей мере от двух точек на границе объекта. Методы выделения контуров условно можно разделить на следующие группы: выделения перепадов яркости; отслеживания (или обхода) контуров; сканирующие. В методах первого класса в окрестностях каждой точки вычисляют градиент перепада яркости. Точки резкого изменения градиента выделяются как контурные Так строится контурная модель, часто состоящая из незамкнутых штрихов. Эти методы используют, в основном, для полутоновых и цветных изображений. На основании такой модели очень трудно описать форму объекта. Поэтому часто исходные изображения сводятся к бинарным. На последних в основном используются методы двух других классов. Методы отслеживания наиболее проработаны и просты в реализации. Обычно сначала выделяются границы, потом выполняется их аппроксимация. Это требует больших затрат памяти и времени. Более универсальный подход - совмещение отслеживания и аппроксимации. Разработаны специальные алгоритмы. Сканирующие методы позволяют выделять контуры объектов при однократном просмотре исходного изображения Для этого используются описания двух соседних строк изображения, списковые структуры. Ряд характеристик объекта удобнее вычислять при растровом представлении. Это площадь объекта, его длина, периметр, центр симметрии дискретного объекта, количество объектов изображения. Разработаны математические методы вычисления этих и других характеристик. Выделение непроизводных элементов производится на основе скелетированного изображения. Фактически данный этап сводится к построению некоторой структуры данных, элементами которой являются выбранные непроизводные элементы и связи между ними Разработаны различные способы представления скелетированных изображений, в специальной литературе даны сведения об их применимости. Растровый формат содержит больше информации о взаимоположении объектов изображения. Это полезно при их распознавании. Векторный формат более экономичен по памяти, более удобен в обработке. Чтобы соединить достоинства обоих форматов из растрового представления извлекают характеристики, используемые для распознавания данных и помещают их в структуру хранения. Возможно, что при этом множество всех характеристик объекта будет избыточным. Сейчас перевод растрового представления в векторное осуществляется не всегда, т.е. формирование векторного представления и связанные с ним операции пропускаются. Третий этап преобразования (Мв—Мп) выполняется с помощью достаточно разработанной теории распознавания образов. Однако существует разрыв между теорией и практикой. Часто в конкретных системах используются технические решения, ориентированные на тот класс объектов, с которым данная система работает. Что касается структур хранения, то современные системы управления базами данных (СУБД) позволяю хранить так называемые BLOB (binare large objects). Конкретный вид бинарной информации при этом значения не имеет. Наиболее распространенные форматы представления изображений будут рассмотрены далее. До сих пор рассматривался процесс получения машинного вида изображения, введенного в компьютер извне. Чтобы создавать изображения некоторого класса на компьютере, требуется другой подход. Рассмотрим общие принципы построения таких моделей графических объектов. Процесс построения делится на 6 этапов: 1. Анализ структуры объекта по принципу иерархии входящих в него элементов с выделением базовых, которые нецелесообразно расчленять далее по соображениям целостности элементов или по характеру задач; 2. Построение математических моделей базовых элементов { Мэi} и представление их в памяти ЭВМ; 3. Анализ структуры объекта с фиксацией всех связей между элементами; 4. Объединение математических моделей базовых элементов для построения математической модели объекта (изображения): Ми = { Мэi}; 5. Дополнение математической модели системными (системообразующими) параметрами { SP }, характеризующими объект как систему взаимосвязанных элементов. Примеры параметров: размеры, определяющие взаимное положение элементов, сведения о предельных отклонениях, условиях сопряжения и т.д.; 6. Объединение в группы GP одинаковых параметров математических моделей элементов с целью минимизации общего объема сведений в математической модели объекта М. Таким образом, математическую модель объекта в общем случае можно представить совокупностью математических моделей элементов, системных параметров и групп параметров: Mи={{Mэi},{SP},{GP}}. К построенной по таким принципам математической модели предъявляются требования: 1. Простота и компактность представления объекта с целью минимизации памяти; 2. Возможность редактирования (дополнение другими элементами, деформирование, выделение сегмента и т.д.), перехода от одних единиц измерения к другим, решения наиболее распространенных задач, связанных с объектом (определение поперечных сечений, моментов инерции, центра тяжести и т.д.); 3. Соответствие представления, объекта возможностям технических средств вывода информации или его преобразование к виду, удовлетворяющему требованиям такого представления. Все перечисленное справедливо, в основном, для векторных моделей, которые широко используются в инженерной практике. Для фотореалистических изображений некоторые требования не нужны, более существенны другие требования, которые будут рассмотрены позже. 14. Понятие аффинных преобразований и их прикладное значение для задач компьютерной графики. Преобразования на плоскости и в пространстве В соответствии с дискретным принципом работы ЭВМ решение любой задачи разбивается на некоторую последовательность шагов (этапов), образующих алгоритм. В компьютерной графике также выделяются элементарные этапы, из которых составляется графический алгоритм (графические преобразования). Основу многих операций компьютерной графики составляют так называемые аффинные преобразования. Греческое слово АФФИНИС означает родственный. Аффинная геометрия - раздел геометрии, изучающий свойства фигур на плоскости и в пространстве, сохраняющиеся при любых аффинных преобразованиях, т.е. инвариантных относительно таких преобразований. Аффинные преобразования обеспечивают точечное взаимно однозначное отображение плоскости или пространства на себя, при котором 3 точкам, лежащим на одной прямой, соответствуют 3 точки, также лежащие на одной прямой. Аффинные преобразования переводят пересекающиеся прямыe в пересекающиеся прямые, параллельные прямые в параллельные прямые. Плоскость аффинно отображается на некоторую плоскость. Существует множество аффинных преобразований. К ним относятся преобразования подобия, сдвиги, сжатия и др. Следовательно, прорисовываются элементарные операции компьютерной графики, не нарушающие геометрических свойств отображаемого объекта. 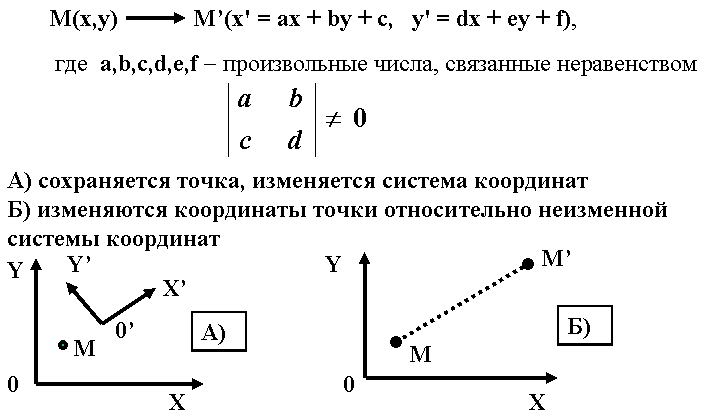 Одной из наиболее простых операций преобразования является пересчет координат точки или перенос системы координат. Пусть имеется точка с координатами (х,у). Поставим этим координатам в соответствие координаты Этот случай можно трактовать двояко: А) сохраняется точка, изменяется система координат Б) изменяются координаты точки относительно неизменной системы координат, т.е. формулы задают отображение, точки М(x,y) в точку М’(x’,y’) в той же координатной системе. Обычно принимается вторая трактовка, т.к. мы работаем в стабильных координатах устройства. В принципе можно строить изображения в любой системе-координат: прямолинейной и криволинейной, прямоугольной и непрямоугольной. Для простоты и в соответствии с привычным представлением будем рассматривать представление в прямоугольной декартовой системе координат.  В машинной графике часто используется матричное представление. Точку можно представить с помощью вектор-столбцов для плоскости |x y|, пространства -|x y z| . Тогда преобразования точек сводятся к операциям над матрицами, что хорошо соответствует возможностям вычислительной техники. В общем виде задача выглядит так. Даны матрицы А и В и задана их взаимосвязь AT = В. Необходимо найти матрицу преобразования. Решением является Т = А-1В, где А-1 - обратная от квадратной матрицы А. Матрица Т - фактически коэффициентов Её можно трактовать и как оператор. Тогда перемножение матриц используется для того, чтобы выполнить геометрическое преобразование над системой точек, представленных с помощью векторов положения отдельных точек, содержащихся в матрице А. Интерпретация матричного умножения как геометрического оператора является основой математических преобразований в машинной графике. В аффинных преобразованиях особую роль играют несколько частных случаев, комбинация которых позволяет описать любое преобразование одной точки в другую в соответствии с формулами (1). Фактически эти случаи описывают конкретный вид матрицы Т, т.е. дают коэффициенты преобразования исходных координат точки. Последовательность выполнения этих преобразований - алгоритмы машинной графики. Начнем рассмотрение элементарных операций с плоскостных. Можно выделить 4 таких операции: поворот, растяжение (сжатие), отражение, перенос. М  атрица преобразования Т при этом имеет вид.Для частного случая поворота на 90° (поворот против часовой стрелки относительно начала координат) вид матрицы | 0 –1 | | 1 0 | Р 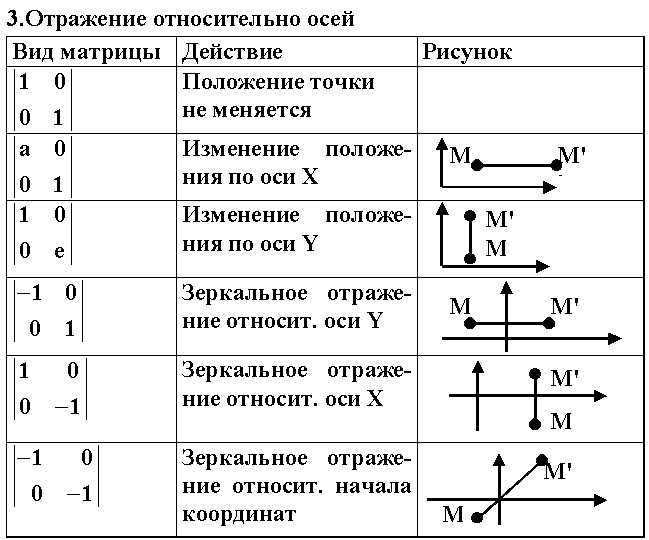 астяжению можно сопоставить положительные, сжатию - отрицательные значения коэффициентов. Другое название операции - изменение масштаба. Как частный случай изменения масштаба можно рассматривать сдвиг вдоль одной из координатных осей. Эти операции перекрываются с ниже рассмотренными операциями зеркального отражения относительно координатных осей.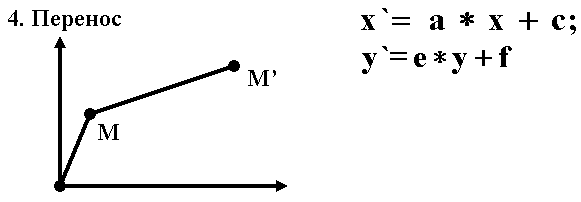 В курсе аналитической геометрии доказывается, что любое преобразование вида (1) всегда можно представить как суперпозицию простейших 4 преобразований, рассмотренных выше. 15. Элементарные аффинные преобразования на плоскости, составляющие базис операций машинной графики. Выше было рассмотрено преобразование точек. Т.к. прямая задается координатами двух ее точек, для операций над прямой также можно использовать умножение матриц. Пусть имеется прямая с координатами концов, заданными векторами А[0,1] и В[2,3]. Возьмем произвольно матрицу преобразования T. Эта матрица осуществляет растяжение (или сдвиг). Выполним операцию умножения для точек А и В. A’=A*T=|3 1|; B’=B*T=|11 7| М  атрица размером 2*2 преобразует любую прямую в другую прямую. Точки результирующей линии взаимно однозначны точкам исходной линии (аффинные преобразования). Можно доказать, что данное утверждение распространяется не только на конечные, но и на серединные и все другие точки отрезка прямой. Для машинной графики существенно, что положение любой прямой линии преобразуется в новое положение преобразованием ее граничных точек и последующим проведением линии между полученными точками. Доказано, что использование матрицы 2*2 для преобразования параллельных линий не нарушает параллельности. Как следствие, в результате действия такой матрицы параллелограмм преобразуется в другой параллелограмм. При преобразовании пересекающихся прямых точка пересечения исходной пары линий преобразуется в точку пересечения результирующей пары. Таким образом, матричное умножение можно использовать для графических построений. Например, можно равномерно или неравномерно менять масштаб фигуры. Если на вершины треугольника воздействует матрица |2 0 0 2| - , координаты увеличиваются в 2 раза. Eсли члены матрицы не равны, фигура искажается.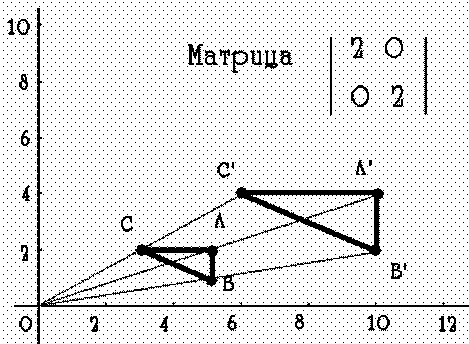 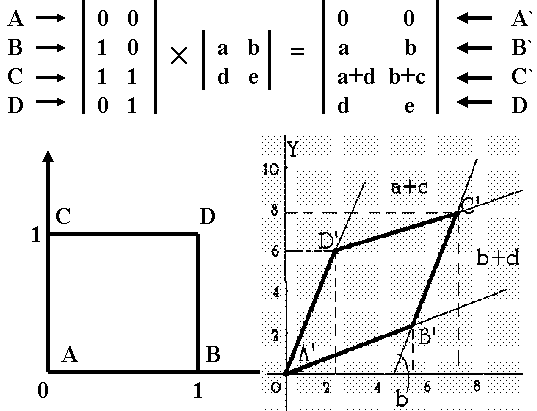 Применение общего матричного преобразования к единичному квадрату с одним углом в начале координат порождает параллелограмм Т.к. конкретный вид матриц преобразования всегда известен, можно посчитать площадь полученной фигуры на основе площади исходной фигуры. 16. Понятие и прикладное значение однородных координат.  Применение матрицы общего вида 2*2 к началу координат дает результат: Таким образом, начало координат инвариантно относительно общего преобразования 2х2. Это является ограничением, которое преодолевается с помощью однородных координат. Пусть М - произвольная точка плоскости с координатами (х,у), вычисленными относительно заданной координатной системы. Однородными координатами этой точки называется любая тройка одновременно неравных нулю чисел x1, x2, х3, связанных с заданными числами соотношением: х1/х3=х; х2/х3=у  Фактически, однородные, координаты дают смещение плоскости, на которой рассматривается фигура, относительно начала координат или, в другой интерпретации, смещение начала координат. Это, по существу, переход к 3-мерному представлению плоских объектов, частный случай пространственного представления.Рассмотрим более подробно. Введем в 2-мерное представление 3 компонент, равный единице. Тогда вектора будут иметь вид: [ х у l ]; [ х' у' l ]. Матрица преобразования примет вид: |10 01 mn| , так как для выполнения умножения матриц число столбцов, описывающих точку, должно равняться числу строк в матрице преобразования. [ х у l ] * |10 01 mn | =[x+m y+n]=[x' у']. Матрица 3*2 не квадратная, поэтому она не имеет обратной матрицы. (Вспомним: даны матрицы А и В, задана их взаимосвязь AT = В. Требуется найти матрицу преобразования. Решением является Т = А-1 В, где А-1- обратная от квадратной матрицы А. Матрица Т - фактически матрица коэффициентов можно трактовать и как оператор.) Чтобы получить квадратную обращаемую матрицу преобразования, дополним ее |100 010 mn1|  Третья (единичная) компонента векторов точек не меняется при добавлении элементов.Полученные результаты можно трактовать как поднятие плоскости, в которой мы работаем, на 1 по оси z.  В более общем случае координаты точки можно представить как (hx, hy, h), h!=0. Следовательно, поднимаем плоскость на h. Практический смысл этого связан с изменением масштаба при вписывании изображения в координаты устройства (мировые координаты -нормированные координаты - координаты устройства). Как правило, координаты устройства являются целыми числами (пикселы), следовательно, точку с координатами (0.5, 0.1, 2.5) представить нельзя. При h=10. получаем (5,1, 25). Другой случай - координаты (80000 40000 1000), что создает угрозу арифметического переполнения. h=0,001 дает (80 40 1).Матрицы третьего порядка позволяют описать любое аффинное преобразование на плоскости. Обычно задачу разбивают на этапы и пользуется 4 элементарными операциями. Матрицы 3 порядка для этих случаев Как использовать эти преобразования? Сначала разбивают действие на элементарные преобразования из 4 приведенных выше, получают матрицы. Потом перемножают эти матрицы в порядке получения. Результирующая матрица является матрицей преобразования. 17. Элементарные аффинные преобразования в пространстве, составляющие базис операций машинной графики. Для пространства однородные координаты выглядят как: (x,y,z,l) или, в более общем случае -(hx,hy,hz,1) Преобразование осуществляется аналогично плоскости по формуле AT = В, но матрица преобразования Т имеет размер 4х4 для однородных координат. Аналогично плоскости любое аффинное преобразование в пространстве представимо как суперпозиции вращений, отражений, растяжений и переносов.  1. Определитель (детерминант) любой матрицы вращения равен 1. Т.к. вращения описываются умножением матриц, трехмерные вращения некоммутативны, т.е. порядок умножения влияет на конечный результат. 4  . 18. Основные виды проекций и соответствующие им аффинные преобразования. Геометрическая операция проектирования (проецирования) выполняет отображение объектов на картинной плоскости. При этом через каждую точку объекта проводятся прямые, начинающиеся в некотором центре. Точки пересечения этих прямых с плоскостью изображения образуют проекцию. Различают проектирование параллельное и центральное. При центральном проектировании все прямые исходят из одной точки - центра пучка К центральным относятся перспективные проекции (прямая - обычная и обратная - иконы). При параллельном проектировании точка центра пучка находится в бесконечности. Каждый из двух основных классов разбивается на несколько подклассов в зависимости от взаимного расположения картинной плоскости и координатных осей.  КЛАССИФИКАЦИЯ ПРОЕКЦИИ
П  ри ортографической проекции картинная плоскость совпадает с одной из координатных плоскостей или параллельна ей. Матрица проектирования вдоль оси хна плоскость yz имеет вид: Е  сли плоскость проектирования параллельна координатной плоскости, матрица [Рx] умножается на матрицу сдвигаПри аксонометрической проекции проектирующие прямые перпендикулярны плоскости отображения. Предмет вместе со связанной с ним системой координат проектируется на некоторую плоскость. В соответствии, с взаимным расположением плоскости проектирования и координатных осей различают проекции: • триметрию (плоскость находится относительно осей координат под различными углами для каждой оси) -. используется редко; • диметрию (два из трех углов между осями и плоскостью равны, т.е. две оси одинаково сокращены); • изометрию (все углы равны, т.е. масштаб по всем осям одинаков). Каждая из этих проекций получается комбинацией поворотов, после чего следует параллельное (ортографическое) проектирование. Можно вывести соответствующие матрицы, некоторые подходы обозначены в [ 1 ]. К  осоугольные проекции используют пучок прямых, не перпендикулярных плоскости отображения. Выделяют два вида косоугольных проекций:• свободную (угол наклона проектирующих прямых к плоскости отображения равен 45°); • кабинетную (частный случай свободной, масштаб по третьей оси в 2 раза меньше). Все это также представимо в матричном виде.  Для свободной проекции а =b = cos / 4. Для кабинетной проекции а = b = 0.5 *cos /4 
Так, при проектировании на плоскость ху точки с координатами х=0, у=0, z=l имеем (0 0 1 l) -> (a b 0 l). Вид матрицы; Перспективные (центральные) проекции более сложны. Они получаются путем перспективного преобразования и проектирования на некоторую плоскость наблюдения. Вводятся параметры, описывающие центр проектирования, т.е. точку, откуда "смотрят" на объект. Пусть эта точка имеет координаты (0 0 с). Тогда матрица перспективного преобразования в пространстве имеет вид: 
В 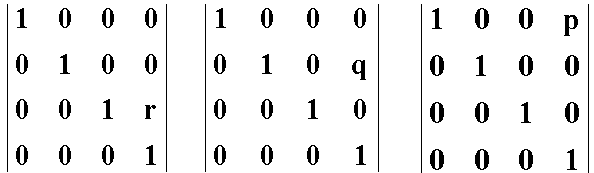 ыкладки получения: Член матрицы, характеризующий местоположение центра проектирования, выводится из уравнения прямой, проведенной из центра проектирования в некоторую точку объекта. Если мы хотим, например, плоскость наблюдения совместить с плоскостью ху, матрица примет вид, значение в третьем столбце третьей строки отражает факт z = 0 . В общем случае при нахождении центра проектирования на осях z или у или х матрицы преобразования будут иметь соответственно вид:Это матрицы одноточечных преобразований. 
Для произвольного центра проектирования с координатами (а, Ь, с) матрица преобразования: Из школьного курса черчения и курса начертательной геометрии известно, что по нескольким проекциям можно восстановить изображение. Для компьютерной графики это соответствует обратным матричным преобразованиям. Т.к. для восстановления изображения используются несколько проекций, преобразования весьма сложны и длительны. Этим объясняется высокая ресурсоемкость подобных задач. Как все это реализовать (запрограммировать)? Здесь удобно использовать объектно-ориентированный подход. Фактически, мы работаем с векторами, т.к. координаты точки - 3 числа. Для класса ВЕКТОР (vector) можно определить систему операций (например, поэлементное сложение и вычитание векторов и т.д.). Определяются также основные функции. Аналогично вводится класс МАТРИЦА (matrix). 19. Геометрические сплайны. В машинной графике часто применяют приближенное изображение фигур. Плавные линии и гладкие поверхности подвергаются кусочно-линейной аппроксимации. Нередко возникает и задача восстановления изображений по известным точкам (сосканированным или полученным иным путем). Один из способов приближенного представления плоских и пространственных изображений - геометрические сплайны. Это отдельное направление компьютерной графики. Рассмотрим его обзорно, на уровне общих понятий. Термин "сплайн" происходит от английского spline. Так называлась гибкая полоска стали, с помощь которой чертежники через заданные точки проводили плавные кривые. Используя теорию упругости, можно доказать, что результирующая кривая приближенно является кусочным кубическим многочленом. Он непрерывен и имеет непрерывные первую и вторую производные. Следовательно, кривая имеет постоянную кривизну и разрывы возникают лишь в третьей производной, что для человеческого глаза практически незаметно. Результирующая кривая или поверхность выглядит гладкой. Если вдоль сплайна совершается механическое движение непрерывность второй производной обеспечивает непрерывность ускорения и, следовательно, отсутствие резки изменений приложенной силы. Это очень важно при механической обработке. Поэтому сплайны используют например, при проектировании траектории движения режущего инструмента. Первая работа по теоретическому исследованию сплайнов вышла в 1946 г. Сначала сплайны рассматривались как удобный инструмент приближения функций Однако быстро обнаружилось множество сплайнов различных типов. Они стали использоваться в численных методах, системах автоматизированного проектирования (САПР), автоматизированных системах технологической подготовки производства (АСТПП) и т.д. Сплайны позволяют заменить аналитическое описание кривых и поверхностей их построением по точкам. Задают несколько точек, лежащих на искомой кривой или поверхности, и через эти точки с помощью сплайнов проводят плавные кривые/поверхности (задача интерполяции). Используют сплайны и для сглаживания. Тогда линию или поверхность проводят вблизи выбранных точек. Возникает задача поиска требуемой сплайн-функции. Для кривых (на плоскости) это задача нахождения сплайн-функции одной переменной. Пусть на плоскости заданы m точек с координатами (х,, у,), i = 0, 1 ,..., m, причем х0 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||