Компьютерная графика контрольная. Вопросы для экзамена по курсу. Вопросы для экзамена по курсу "Компьютерная графика"

• Название: Вопросы для экзамена по курсу "Компьютерная графика"
• Анкор: Компьютерная графика контрольная
• Дата: 31.07.2022
• Размер: 278.18 Kb.
• Имя файла: Вопросы для экзамена по курсу.docx
• Тип: Вопросы для экзамена; #638568
• страница: 3 из 3

<...<xm

(точки упорядочены по возрастанию абсциссы). Для этого набора требуется найти сглаживающего кривую, мак­симально приближенную к исходным точкам. Здесь возможны две крайности:

1. Кривую можно провести непосредственно через исходные точки. Тогда получаем интерполяцию с помощью ломаной. Достоинство: простота, постепенность построения (поэтапность). Недостаток: отсутствие гладко­сти. даже первая производная имеет разрывы в узлах;

2. Из курса математического анализа известно, что существует интерполяционный многочлен Лагранжа, гра­фик которого проходит через все заданные точки.

г 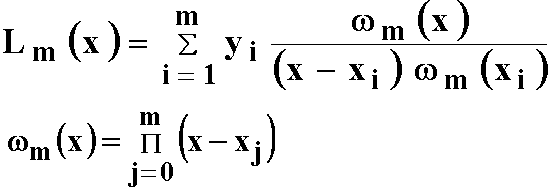де (х, у,) i = 1 .. m - заданные точки

Достоинство: относительная простота описания, удобство подсчета коэффициентов. Недостаток: изменение од­ной точки влечет пересчет всех коэффициентов многочлена. Такое изменение весьма влияет и на вид кривой

Сплайны сохраняют достоинства и уменьшают недостатки обоих подходов Они строятся с помощью многочленов (второй подход), но последовательно (первый подход) При этом важно определить степень каждо­го многочлена и подобрать его коэффициенты так, чтобы обеспечить гладкое сопряжение соседних звеньев,

К 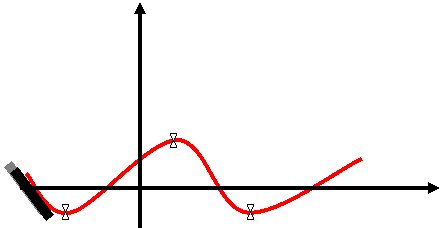ак это соотносится с происхождением названия "сплайны"? Если гибкую стальную линейку поставить на ребро, закрепить в крайней точке последовательности и разместить так, чтобы она проходи ла через остальные точки, получим некоторую функцию, описываюшую профиль этой линейки.


Эта функция обладает свойствами:

• с довольно большой точностью часть графика этой функции, заключенного между любыми 2 соседними точками, можно считать многочленом третьей степени;

• на всем промежутке от начальной до конечной точки эта функция дважды непрерывно дифференцируема

Полeченная функция называется интерполяционным кубическим сплайном.

Более точная формулировка:

ИНТЕРПОЛЯЦИОНЫЙ КУБИЧЕСКИЙ СПЛАЙН - функция S(x), обладающая свойствами: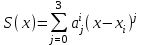

1. 
   Г рафик функции S(x) проходит через каждую точку заданного массива, т.е. S(xi)=yi, i=0..m;
   

На каждом из отрезков [xi, xi+1]i=0,1,..m-1 функция является многочленом третьей степени

3. На всем отрезке задания (x0, xm) функция S(x) имеет непрерывную вторую производную.

Т.к. на каждом из отрезков [хi хi+1,] сплайн S(x) определяется 4 коэффициентами, для его полного построения необходимо найти 4*m чисел. Эти коэффициенты ищутся, исходя из условия 3, т.е. непрерывности сплайна во всех внутренних узлах, а также непрерывности первой и второй производной. Условия непрерывности накладывают ограничения на коэффициенты. Следовательно, для их определения получаем для всех внутренних узлов 4*m - 2 равенств. Недостающие граничные условия можно получить, задав, например, значения первых производных на концах интервала x0и xm. Могут быть и граничные условия других типов. Таким образом, для определения коэффициентов решается система линейных уравнений.

Для изображений в пространстве нужно построить поверхность, проходящую через данные точки пространства. Используется функция 2 переменных, т.е. интерполяционный бикубический сплайн. ИНТЕРПОЛЯЦИОННЫЙ БИКУБИЧЕСКИЙ СПЛАЙН - функция 2 переменных S(x,y). обладающая свойствами:

1 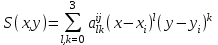. График функции S(x,y) проходит через каждую точку заданного массива, т. S(xi,yj)=Zij, i=0..m,j=0..n;

2. На каждом из прямоугольников |xi,xj+i]*[yj,yj+1,], i=0..m-l, j=0..n-l функция является многочленом 3-ей степени по каждой из переменных:

3. На всем прямоугольнике задания |x0,xm]*[y0,yn,] функция S(x,y) имеет по каждой переменной непрерывную вторую производную.

Количество коэффициентов бикубического сплайна равно 16*m*n . Как и для одномерного случая, для получения коэффициентов строится система линейных уравнений.

Достоинство сплайнов - относительная простота. Методы решения систем линейных уравнений хорошо известны. Недостаток: изменение хотя бы одной точки влечет большой объем пересчета коэффициентов. Если точки задаются приближенно, нет необходимости жесткого прохождения функции через каждую точку, можно использовать методы сглаживания. Это ведет к тому, что ослабляется требование однозначного проектирована искомой кривой на координатную ось или поверхности на координатную плоскость. Таким образом, кривая может быть замкнутой, самоперссекающейся и т.д., возможно несколько проходов по одним и тем же точкам при формировании изображения, ослабляются требования к задаваемому массиву исходных точек.

Пусть в пространстве (или на плоскости) задан упорядоченный набор точек, определяемый векторами V0-V1-…-Vm. Ломаная V0-V1-…-Vm назы­вается контрольной ломаной, порожденной массивом V = {Vo,V1,...Vm}.

Если рассмотреть для начала наиболее простой двумерный вариант, то ставится задача нахождения сглаживающей кривой. В качестве одной из таких кривых может выступать кривая Безье.

Математически кривая Безье описывается полиномиальной функцией, которая осуществляет интерпо­ляцию между начальной и конечной точками интервала. Кривая Безье является гладкой и катается начального (V0 -Vi) и конечного (Vm-1-Vm) отрезков контрольной лома­ной. Каждый член полинома соответствует одной из точек интервала. Точки могут рассматриваться в любом порядке, а не только по возрастанию одной из координат). Следовательно, в зависимости от порядка точек по­лучаются разные кривые. Пример - для 4 точек (кубическая кривая Безье):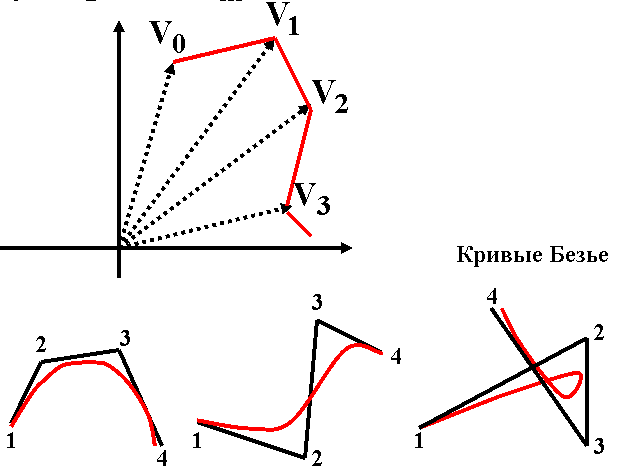

Кроме достоинств (гладкость, известные, хорошо реализуемые методы расчета коэффициентов) кривые Бе­зье имеют и общие для сплайнов недостатки:

• степень коэффициентов полинома на 1 меньше количества точек, т.е. зависит от количества точек

• изменение хотя бы одной точки приводит к изменению вида кривой, при добавлении/изменении хотя бы одной точки набора требуется пересчет всех коэффициентов.

На практике применяют построение кривой по фрагментам, выбирая, как правило, по 4 точки, т.е пользуясь кубическими кривыми Безье. Чтобы фрагменты хорошо сопрягались, на исходные точки накладывается ряд условий. Например, необходимо, чтобы каждые 3 соседние точки лежали на одной прямой.

Как улучшить результаты, получаемые с помощью кривых Безье? В уравнении, задающем кривую Безье, векторные составляющие (координаты точек опорного массива) постоянны, пока мы их не захотели изменить. Следовательно, улучшение возможно за счет коэффициентов многочлена (изменяем способ их подсчета).

Класс сплайновых кривых гораздо шире кривых Безье. Кривые Безье относятся к классу полиномов Бернштейна (строятся в базисе Бернштейна). Существует другой базис, называемый В-сплайн базисом (от base - базовый), для которого базис Бернштейна является частным случаем. Здесь принят иной способ вычисление коэффициентов. Причем эти коэффициенты не зависят от координат конкретных точек четверки. Коэффициен­ты вычисляются по рекуррентным (рекурсия!) формулам. Поэтому изменение одной вершины исходного массива не влечет полный пересчет всех коэффициентов. Пересчитывается только некоторая часть из них (5 слагае­мых). Здесь также ограничиваются обычно кубическими многочленами, т.е. используют кубические В-сплайны.

Часто возникает желание подправить построенную с помощью В-сплайнов кривую без изменения мас­сива опорных точек. Для этого в уравнение кривой вводятся параметры. Таким образом получаются обобщение кубических В-сплайнов, называемые рациональными кубическими В-сплайнами и бета-сплайнами.

В рациональных кубических В-сплайнах каждый коэффициент умножается на вес (параметр формы) - не­отрицательное число. Сумма этих чисел положительна (т.е. по крайней мере одно из чисел ненулевое). Если все веса равны между собой, получаем элементарную кубическую В-сплайновую кривую.

В бета-сплайнах весовые коэффициенты (в формулах для которых присутствует обозначение бета) ищутся исходя из условий гладкости в точках сопряжения частичных кривых. Математические формулы, обеспечи­вающие это свойство, известны (непрерывность функции, первой и второй производной). Следовательно, путем ряда математических преобразований ищутся коэффициенты многочленов, в состав которых входят 2 числовые параметра. Эти параметры называются параметрами формы бета-сплайновой кривой: (1 - параметр скоса. (2- параметр напряжения (1 > 0, 2 >= 0). При 1 = 1, 2 = 0 получается кубическая В-сплайновая кривая.

Для поверхностей добавляется еще одна координата. Следовательно, вместо контрольной ломаной получа­ется контрольный многогранник, а точнее - опорный граф заданного массива точек. Построение ведется по элементарным фрагментам, которые задаются не 4, а 16 точками, т.к. имеем дело с плоскостями, составляющи­ми контрольный многогранник. Сглаживающие поверхности строятся на тех же принципах, что и сглаживаю­щие кривые: построение ведется по фрагментам, используются бикубические многочлены. Получаются бикуби­ческие поверхности Безье, бикубические В-сплайновые поверхности. Они наследуют основные свойства одно­именных кубических кривых применительно к поверхностям.

20. Алгоритм Брезенхема.

Подавляющее большинство графических устройств - растровые, т.е. изображение представляется в ви­де матрицы или решетки пикселов (растра). Это требует специальных алгоритмов аппроксимации изображений.

Растр можно представить решеткой, состоящей из единичных квадратов. Центр каждого квадрата - ко­ординаты соответствующего пиксела. Когда инициализируется точка с координатами (p,q), вся ее квадратная окрестность закрашивается каким-либо цветом.

Плавно изогнутые линии подвергаются кусочно-линейной аппроксимации, минимальный шаг - 1 пик­сел. Возможность соединения двух пикселов растровой линией называется СВЯЗНОСТЬЮ. Растровая линия – суть последовательный набор соседних пикселов. Пусть есть 2 пиксела с координатами Pl(xl,yl) и Р2(х2, у2).

Методы получения растрового приближения геометрических фигур различны, т.к. одну фигуру

можно представить неоднозначно. Это касается, в основном, граничных точек.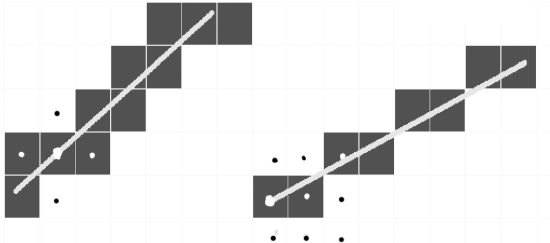

Можно строить 4-и 8-связное представление. Возможны и другие растровые модели. Все зависит от того, какими свойствами требуется наделить полученный образ.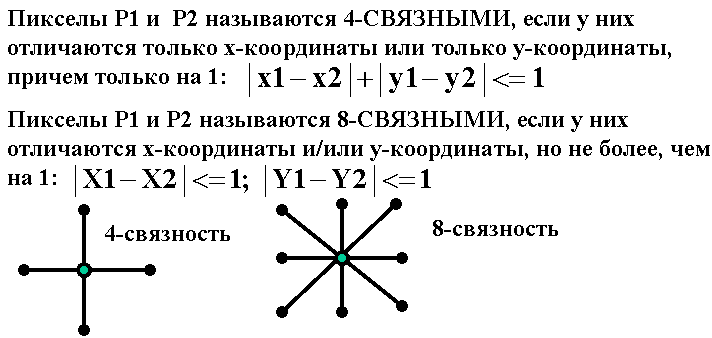



Очевидное решение - инициировать последовательно все точки растра, квадратные окрестности которых пересекают данный отрезок. Результатом является 4-связная растровая развертка отрезка. 8-связная решетка включает те точки растра, боковые стороны квадратных окрестностей которых пересекаются с отрезком.

П 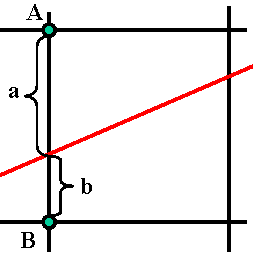усть отрезок имеет координаты концов M(xl,yl) и М2(x2,у2). Уравнение прямой y=k*x+b. Для простоты предположим, что угловой коэффициент 0 < k <= 1 (k не отрицателен и не превосходит 1), т.е 0<=(y2-yl)<=(x2-xl). Уравнение отрезка имеет вид y =k*(x-xl)+yl, где k = (y2-y1)/(x2-x1).

В 1965 г. Брезенхейм (Bresenham) предложил простой целочисленный алгоритм растрового построения отрезка. Сначала он использовался в графопостроителях. Алгоритм основан на том, что при построении всегда берется ближайший по вертикали пиксел, т.е. точка, ближайшая к исходной прямой. Очевидная оценка близости: если отклонение исходной прямой по оси ординат от текущего значения превышает 0.5, увеличиваем координату у на 1, корректируем текущее значение отклонения. Чтобы перейти к целочисленным расчетам, изменяют масштаб, умножая отклонение и приращение по оси у d =(y2-y1)/(x2-x1) на некоторое целое 2*n . В качестве n естественно выбирается величина х2-х1, т.е. отклонение вычисляется как d =(х2-х1)*(b-а). Если d>0, значение у увеличивается на 1, иначе – не изменяется. d при этом уменьшается на "масштабированную" единицу, (вместо у=у-1 пишем у=y+2*((y2-yl)-(x2-xl))) или увеличиваетcя на величину "масштабированного" приращения (вместо у=у+ ((y2-yl)/(x2-xl)) пишем у = y+2*(y2-yl)).

До сих пор рассматривался случай 01 переменные х и у меняются местами.