Теор вопрос. Теор. вопросы 1. Вопросы к экзамену по анализу, 1 семестр Докажите, что множество всех интервалов (ав) с рациональными концами счетное
 Скачать 44.71 Kb. Скачать 44.71 Kb.
|
|
Теоретические вопросы к экзамену по анализу, 1 семестр 1. Докажите, что множество всех интервалов (а;в) с рациональными концами счетное. 2. Докажите, что множество попарно не пересекающихся интервалов на действительной оси, конечное или счетное. 3. Множество всех последовательностей, состоящих из нулей и единиц, имеет мощность континуума. 4. Приведите пример последовательности, имеющей три предельных точки. 5. Множество рациональных чисел счетное, поэтому существует последовательность, членами которой являются все рациональные числа. Какое множество предельных точек такой последовательности. 6. Доказать, что если последовательность 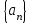 сходящаяся, то последовательность сходящаяся, то последовательность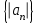 также сходящаяся. также сходящаяся.7. Справедливо ли утверждение: сумма двух бесконечно больших последовательностей является бесконечно большой последовательностью? (обосновать) 8. Доказать, что произведение двух бесконечно больших последовательностей есть бесконечно большая последовательность. 9. Верно ли утверждение: произведение б.м.ф. на б.б.ф. есть ограниченная функция? 10. Может ли функция в одной точке быть б.м., а в другой – б.б.ф? 11. Всегда ли сумма двух бесконечно больших функций является бесконечно большой функцией? 12. Сформулируйте понятие 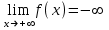 . .13. Сформулируйте понятие 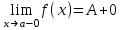 . .14. Докажите, что кубическое уравнение всегда имеет корень. 15. Докажите, что функция 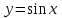 непрерывна в точке непрерывна в точке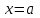 . .16 Приведите пример непрерывной неограниченной на интервале 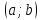 функции. функции.17. Докажите, что 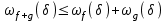 . .18.Докажите, что 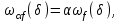 для для 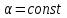 19. Докажите, что 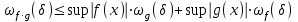 20 Докажите непосредственно, что 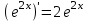 . .21. Найдите функцию обратную к функции 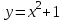 на на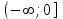 . .22. Функция 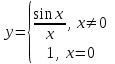 . Найдите производную функции в точке . Найдите производную функции в точке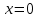 . .23. Постройте для функции 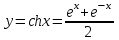 , определенной на , определенной на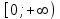 , обратную функцию и найдите ее производную. , обратную функцию и найдите ее производную.24. Неявную функцию, заданную уравнением 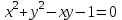 , записать в параметрической форме и найти ее производную в точке , записать в параметрической форме и найти ее производную в точке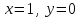 . .25. Пусть 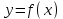 определена на отрезке определена на отрезке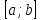 и при любых и при любых 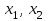 из этого отрезка выполняется неравенство: из этого отрезка выполняется неравенство: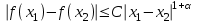 , ,  . Доказать, что функция . Доказать, что функция  постоянная. постоянная.26. Каково поведение функции в окрестности точки  , если , если  , а , а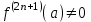 ? ? |
