Теория автоматов. Ответы на вопросы экзамена. Теория автоматов ответы к экзамену. Вопросы к экзамену Строки. Префиксы, суффиксы, подстроки. Формальные языки
 Скачать 4.63 Mb. Скачать 4.63 Mb.
|
|
_____________________Вопрос 37____________________ Соединение автоматов с обратной связью. Соединения с обратной связью: 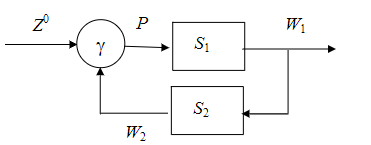 Хотя бы один должен быть автоматом Мура. 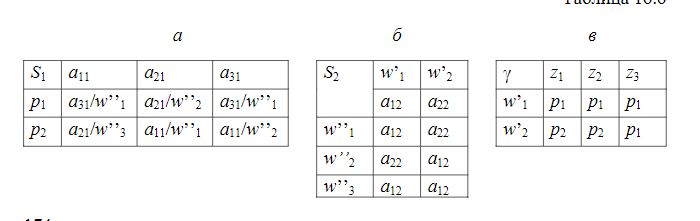  
Синтез схем по временным булевым функциям(ВБФ) Работа реальных автоматов, происходит во времени, чтобы описать работу реальных автоматов вводят понятие автоматного времени. Вводит в себя последовательность временных интервалов на к-е разбито все время работы автомата. S- число интервалов. 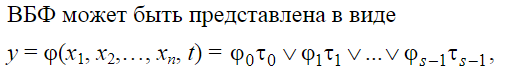 Синтез: строим временную диаграмму. Сколько проводов, столько интервалов. Функцию По уравнениям строим логическую схему, реализующую ВБФ. ___________________Вопрос 39____________________ Синтез и анализ последовательностных автоматов. РБФ - лог. ф-я, зависящая от текущих и от предшествующих значений ф-ци. Значения y(t+1) получаются задержкой сигнала y(t) на J тактов с помощью операторов задержки D. x-входные переменные, у- сигналы обратной связи. Пример, поступают только сигналы обратной связи. 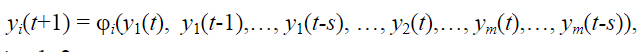 Задание РБФ всегда должно происходить с оговоренными начальными условиями. Пусть обратная связь осуществляется с задержкой на 1 такт, тогда: 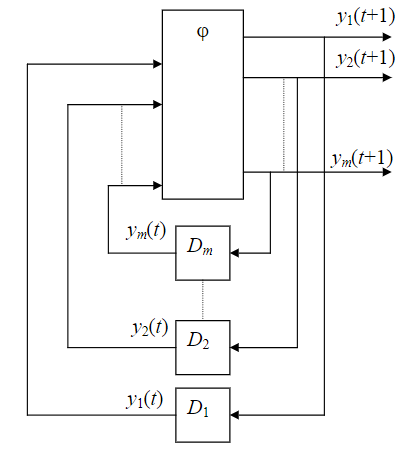 Схемы описываемые уравнениями Чтобы провести анализ последовательностной схемы, необходимо: получить мат. модель По полученной математической модели, строим таблицу истинности по таблице истинности и начальным условиям строим таблицу переходов. выявляем наличие циклов Строим круговую диаграмму Выписываем циклы и тупиковые состояния Все состояния автомата должны быть проверены на тупиковые состояния, если имеется хотя бы 1 такое состояние, необходимо предусмотреть меры, обеспечивающие невозмножность попадание в него. ___________________Вопрос 43____________________ Определение абстрактного автомата. Автоматы Мура и Мили. Абстрактная теория изучает лишь переходы, к-е выполняет автомат под воздействием входных сигналов и те выходные сигналы, к-е он выдает. Не рассмат-я структуру автомата. Абстрактный автомат имеет один вход и один выход. Абстрактный автомат- мат. модель дискретного устройства, заданная: : S=(A,Z,W,сигма,лямда,а0) : 1. A={a1, a2, ... ,am} - множество состояний автомата 2. Z={z1, z2, ... ,zf} - множество входных сигналов 3. W={w1, w2, ..., wg} - множество выходных сигналов 4. сигма- функция переходов, показыв в какое сост аs перейдёт авт-т,находясь в сост am ,при входном сигнале zf . 5. лямда - функция выходов,показ. в какой выходной сигнал вырабатыв на выходе авт-та am под действием сигнала zf 6. a0 - начальное состояние автомата.  Абстрактный автомат называется конечным, если конечны множества А = {a1, a2, ..., am}, Z = {z1, z2, ..., zf}, W = {w1, w2, ..., wg}. Автомат называется конечным, если множество его внутренних состояний, а также множества значений входных и выходных сигналов конечны. Конечный автомат в графическом представлении-это направленный граф,имеющий один начальный и один или несколько конечных узлов. В каждый момент t дискретного времени автомат находится в некотором состоянии a(t) из множества состояний автомата, причем в начальный момент t = 0 он всегда находится в начальном состоянии a(0)=a1. В момент t, будучи в состоянии a(t), автомат воспринимает сигнал z(t) на входном канале, и вырабатывает на выходном канале сигнал W(t)=лямда(a(t), z(t)) и в соответствии с функцией переходов перейдет в следующее состояние a(t+1)=сигма[a(t), z(t)] Распространенные Мили и Мура. Мили(1ый род R): 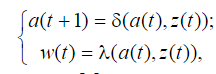 Мура(2ой род S): 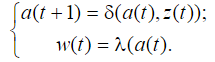 Видно, что, в отличие от автомата Мили, выходной сигнал в автомате Мура зависит только от текущего состояния автомата и в явном виде не зависит от входного сигнала. Видно, что, в отличие от автомата Мили, выходной сигнал в автомате Мура зависит только от текущего состояния автомата и в явном виде не зависит от входного сигнала. Автомат Мура можно рассматривать как частный случай автомата Мили, имея в виду, что последовательность состояний выходов автомата Мили опережает на один такт последовательность состояний выходов автомата Мура, т.е различие между автоматами Мили и Мура состоит в том, что в автоматах Мили состояние выхода возникает одновременно с вызывающим его состоянием входа, а в автоматах Мура - с задержкой на один такт, т.к в автоматах Мура входные сигналы изменяют только состояние автомата. ___________________Вопрос 44____________________ Способы задания автоматов. Табличный метод: Мили задается двумя таблицами 1ая сигма, 2ая лямда. 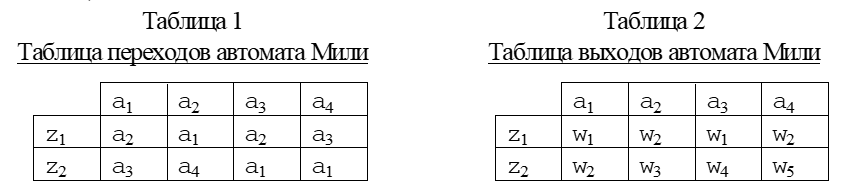 Часто эти две табл совмещ в одну и она наз совмещённой табл переходов-выходов: 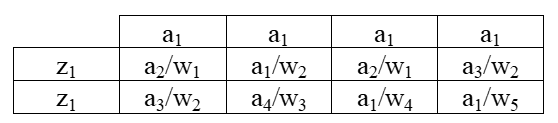 Поскольку в автоматах Мура выходной сигнал зависит только от состояния, он задается только одной таблицей. 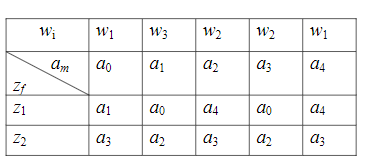 Графический метод: Задается в виде ориентированного графа, вершины которого соответствуют состояниям, а дуги - переходам между ними. Дуга, направленная из вершины am, задает переход в автомате из состояния am в состояние as. В начале этой дуги записывается входной сигнал Zf, вызывающий данный переход as=сигма(am,zf). Для графа автомата Мили выходной сигнал wg формируемый на переходе, записывается в конце дуги, а для автомата Мура - рядом с вершиной am, отмеченной состоянием am, в котором он формируется. 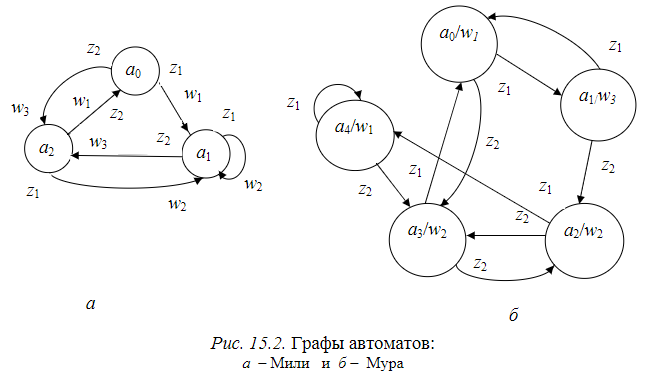 Автоматы могут быть заданы с помощью матриц: Читается так, из состояния а0 в состояние а1 переходит под действием сигнала z1, при этом вырабатывается выходной сигнал w1. 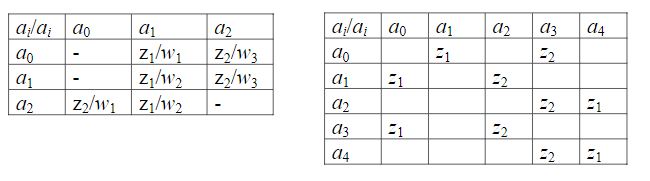 ___________Вопрос 45(совпадает с 21, читай выше)___________ Вопрос 46 Структурный автомат, интерпретация состояния автомата состояниями элементов памяти. Как реализовать автоматы в реальности? Чтобы ответить на этот вопрос, необходимо понимать, что мы не может просто так взять абстрактный конечный автомат(Мура или Мили) и вставить его в железку. Нужно иметь представление о структурном типе автоматов. В самом слове «структура» уже кроется смысл. Структурный автомат состоит из комплекса элементов: абстрактный конечный автомат(комбинационная часть) и и память, об этом гласит Теорема Глушкова. Что можно нужно уметь делать со структурным автоматом? Нужно уметь синтезировать комб часть, а также определять какие элементы памяти использовать и сколько таких элементов нам необходимо. ___________________Вопрос 47____________________ Элементарные автоматы RS-, D-, DV- триггеры. Триггер - устройство, имеющее 2 устойчивых состояния, в к-е он переходит под действием определенных входных сигналов. D-триггер – элемент задержки – имеет один информационный вход D и один выход Q и осуществляет задержку поступившего на его вход сигнала на один такт. 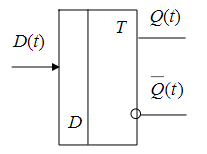 Граф 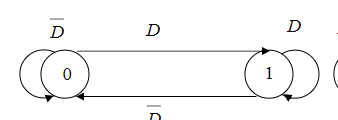 RS-триггер – триггер с раздельными входами.Данный триггер имеет два входных канала R и S и один выходной Q. Вход S (set) называется входом установки в единицу, вход R (reset) – входом установки в нуль. 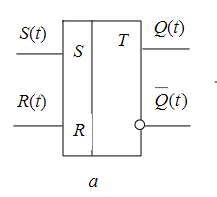 Граф, описывающий поведение RS триггера 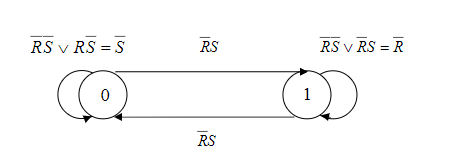 На основе графа может быть составлена таблица, в к-й указаны значения входов для осуществления всевозможных переходов триггера. 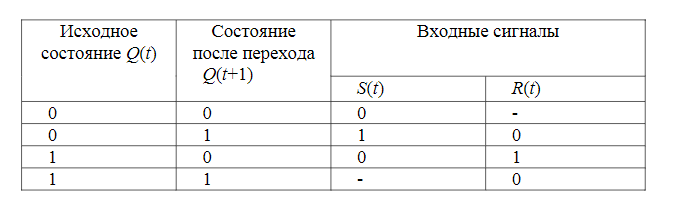 DV- триггер DV- триггер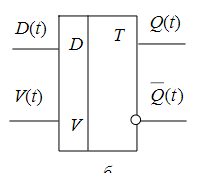 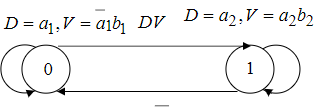 ___________________Вопрос 48____________________ Элементарные автоматы JK-, T- триггеры. 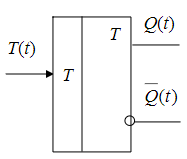 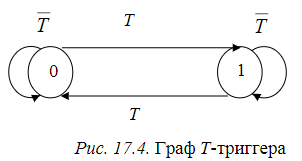 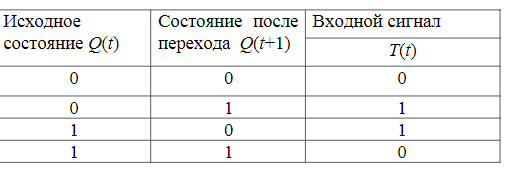 T триггер реализует 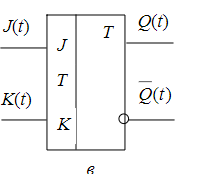 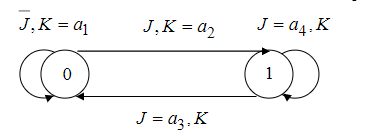 ___________________Вопрос 49____________________ Реакции автомата Мили и Мура. Реакции автоматов Мили и Мура на входные сигналы имеют различное представление. Пусть цепочка выходных данных имеет вид: Z=z1z2z1z2z2  После окончания входной цепочки Мили находится в нек-м состоянии и выходной сигнал не вырабатывается, а в Мура находится в нек-м состоянии и вырабатывает выходной сигнал. Каждому автомату Мура можно поставить в соответствие Мили и наоборот. На примере видно, что реакции автоматов совпали. В Мура начальный выходной сигнал не учитывается. Вопрос 50 Распознаватели цепочек Есть конечный автомат с начальными состояниями и с конечным состоянием(обозначали диезом) автомат должен ответить на вопрос, правильная цепочка, она принадлежит грамматике или нет. Есть контекстная, контекст-свободная и регулярная грамматика. Если цепочка входит в грамматику, то она переводит автомат в другое конечное состояние, значит это правильное состояние, автомат ее распознал. Если она неправильная, то автомат ее распознал и сказал, что она не подходит. Цепочка есть слово, принадлежащее заданному алфавиту. К примеру: Пусть имеется автомат DFA. Σ={0,1} - алфавит нашего автомата DFA, состоящий из 2 букв(0 и 1) Язык определяет грамматику. Язык алфавита определяется буквой L(language). L(DFA) = {w| w начинается с 1} - это читается как: языком автомата являются слова такие, что начинаются с 1. Построим автомат DFA: 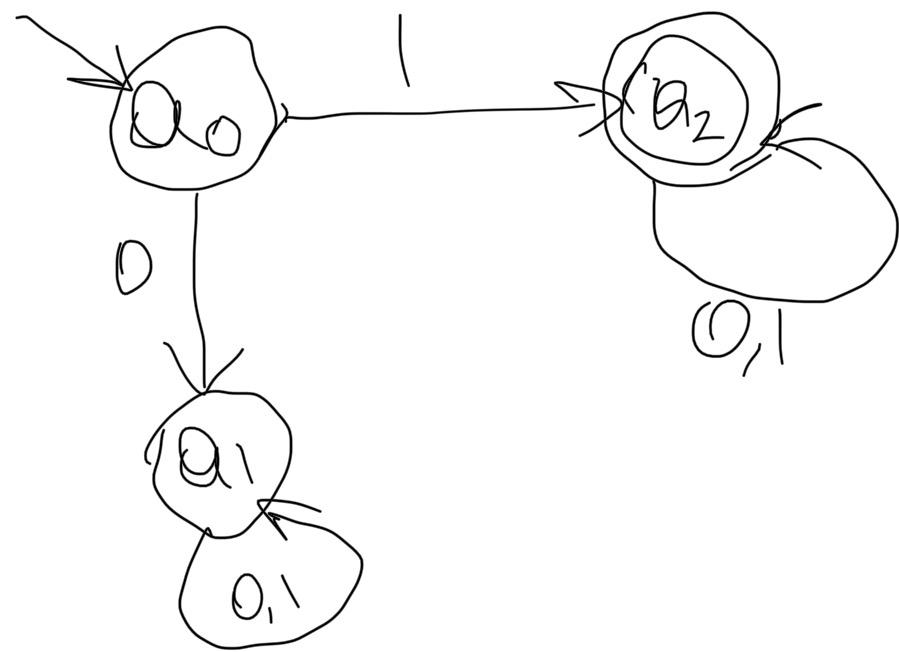 a0 - начальное состояние автомата; a1 - состояние, в которое автомат переходит, в случае, если первая буква в слове не является 1; а2 - конечное состояние(обведено двумя кругами) автомат переходит в это состояние ТОГДА и только ТОГДА, КОГДА первая буква в слове 1. В случае, если автомат остановится здесь, в состоянии а2, мы можем твёрдо утверждать, что заданное слово принадлежит регулярному языку. Например, подадим на вход автомата слово 100. Когда указатель будет на букве 1 нашего слова 100, автомат перейдёт из состояния а0 в состояние а2. После, указатель окажется на первом нуле нашего слова 100. С этого момент автомат зациклится на состоянии а2 и самое главное, он остановится на финишном состоянии. Что было бы, если бы на вход было подано слово 01? Автомат сразу перешёл бы в состоянии а1 и оттуда он уже не выйдет. Он остановится на нефинишном состоянии, значит слово 01 не принадлежит регулярному языку, поскольку автомат не считал слово. |
