Баскаков. Вопросы по курсу обыкновенные дифференциальные уравнения
 Скачать 10 Kb. Скачать 10 Kb.
|
|
ВОПРОСЫ ПО КУРСУ «ОБЫКНОВЕННЫЕ ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ» Третий семестр. Лектор А.В. Баскаков (Поток Костин-Баскаков) Основные понятия, относящиеся к ОДУ 1-го порядка: частное и общее решения, частный и общий интеграл, интегральные кривые. Задача Коши, ее геометрический смысл. Формулировка теоремы существования и единственности решения задачи Коши (ТСЕ) для ОДУ 1-го порядка. Уравнения с разделяющимися переменными. Уравнения, приводящиеся к уравнениям с разделяющимися переменными. Линейное однородное уравнение первого порядка. Вид общего решения. Линейное неоднородное уравнение первого порядка. Метод вариации постоянной. Уравнение Бернулли. Уравнения в полных дифференциалах. Критерий уравнения в полных дифференциалах. Уравнения, сводящиеся к уравнениям полных дифференциалов. Интегрируемый множитель. Поиск и.м. в частных случаях. Уравнения первого порядка, не разрешенные относительно производной. Метод введения параметра. Уравнения Лагранжа и Клеро. Основные понятия, относящиеся к ОДУ n-го порядка: частное и общее решения, частный и общий интеграл, интегральные кривые. Задача Коши, ее геометрический смысл. Формулировка теоремы существования и единственности решения задачи Коши (ТСЕ) для ОДУ n-го порядка. Простейшие ОДУ n-го порядка, допускающие понижение порядка. Однородное линейное ОДУ n-го порядка. Свойство линейности решений однородного уравнения. Линейно зависимые (л.з.) и линейно независимые (л.н.в.) системы функций. Определитель Вронского произвольной системы функций. Теорема о его равенстве нулю. Свойства определителя Вронского решений однородного линейного ОДУ n-го порядка. Критерий л.н.з. решений. Свойства комплексных решений однородного линейного ОДУ n-го порядка с вещественными коэффициентами. Неоднородное линейное ОДУ n-го порядка. Теорема об общем решении. Неоднородное линейное ОДУ n-го порядка. Метод вариации постоянных. Теоремы о частном решении однородного линейного ОДУ n-го порядка с постоянными коэффициентами и о ФСР в случае простых корней характеристического уравнения. Построение ФСР однородного линейного ОДУ n-го порядка с постоянными вещественными коэффициентами в случае кратных и комплексных корней характеристического уравнения (на примере). (б.д.) Неоднородное линейное ОДУ n-го порядка с постоянными коэффициентами Случай специальной правой части. Принцип суперпозиции. Системы линейных ОДУ 1-го порядка. Общее и частное решения, интегральная и фазовая кривые. Задача Коши, ее геометрический смысл. Формулировка ТСЕ. Однородные системы линейных ОДУ 1-го порядка. Свойство линейности решений однородной системы. Линейно зависимые (л.з.) и линейно независимые (л.н.з.) вектор-функции. Определитель Вронского произвольной системы вектор-функций. Теорема о его равенстве нулю (с док-вом). Свойства определителя Вронского решений однородной системы линейных ОДУ 1-го порядка. Критерий л.н.з. решений (без док-ва). Свойства комплексных решений системы линейных ОДУ 1-го порядка с вещественными коэффициентами. Переход от комплексной ФСР к вещественной. Неоднородные системы линейных ОДУ 1-го порядка. Теорема об общем решении. Метод вариации постоянных. Понятие функциональной зависимости функций. Определитель Якоби. Теоремы о функциональной зависимости (б.д.) Понятие первого интеграла систем уравнений. Критерий первого интеграла. Теорема об (n-1) независимых первых интегралов систем. Однородные и неоднородные уравнения в частных производных I порядка. Решение уравнения. Понятие характеристической системы для однородного уравнения. Общее решение однородного уравнения в ч.п. I пар. Задача Коши. ТС и Е (б.д.) Квазилинейное уравнение в ч.п. I порядка. Эквивалентное данному уравнению однородное уравнение с ч.п. Числовые ряды Сходимость и сумма числового ряда (ч.р.). Критерий Коши и необходимое условие сходимости ч.р. Критерий сходимости ч.р. с неотрицательными членами. Признак сравнения в допредельной и предельной формах. Интегральный признак Коши – Маклорена. Признак Даламбера в допредельной и предельной формах. Радикальный признак Коши в допредельной и предельной формах. Абсолютная и условная сходимость ч.р. Преобразование Абеля. Признаки Дирихле и Абеля. Признак Лейбница, оценка остатка. Функциональные последовательности и ряды Поточечная и равномерная сходимость (р.сх.) функциональной последовательности и функционального ряда (ф.р.) на множестве Х. Критерий р.сх. функциональной последовательности (ф.п.). Критерий Коши р.сх. ф.п. (ф.р.). Необходимое условие р.сх. ф.р. Признак Вейерштрасса р.сх. ф.р. Преобразование Абеля. Признаки Дирихле и Абеля р.сх. ф.р. Теорема о предельном переходе для р.сх. ф.п. (ф.р.). Непрерывность предельной функции в точке и на отрезке для р.сх. ф.п. (ф.р.) Интегрирование и дифференцирование р.сх. ф.п. (ф.р.) Степенные ряды Первая теорема Абеля. Радиус, интервал сходимости степенного ряда (ст.р.). Теорема Коши – Адамара. Равномерная сходимость ст.р. и непрерывность его суммы. Единственность разложения в степенной ряд. Равномерная сходимость ст.р., сходящегося при x = R. Вторая теорема Абеля. Почленное интегрирование и дифференцирование степенных рядов. Ряд Тейлора функции 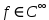 , его коэффициенты и единственность разложения. Критерий разложимости функции в ст.р. (ряд Тейлора). , его коэффициенты и единственность разложения. Критерий разложимости функции в ст.р. (ряд Тейлора).Разложение функций 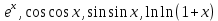 в ряд Тейлора с указанием радиуса и множества сходимости. в ряд Тейлора с указанием радиуса и множества сходимости. |
