Вопросы по теории линейных операторов к Домашней работе 3.
Дать определение инвариантного подпространства линейного оператора. Описать инвариантные подпространства оператора проектирования на координатную плоскость в пространстве R3.
Линейное подпространство L V называется инвариантнымподпространством оператора , если из x L следует , что (x) L.
V = R3, – оператор ортогонального проектирование на плоскость OXY. Опишем инвариантные подпространства этого оператора. Это- всё пространство R3 ,нулевое подпространство {0} , плоскость OXY, прямые, лежащие в плоскости OXY и проходящие через начало координат, ось OZ, плоскости, проходящие через осьOZ.
Дать определения собственного вектора и собственного значения линейного оператора. Привести пример оператора, у которого нет собственных векторов и оператора, у которого любой ненулевой вектор – собственный.
Ненулевой вектор x называется собственным вектором оператора , если (x) = λx. Число λ из рассматриваемого поля называется собственным значением оператора , соответствующим собственному вектору x.
Пример оператора, у которого нет собственных векторов и оператора, у которого любой ненулевой вектор – собственный.
Дать определение собственных подпространств линейного оператора. Описать собственные подпространства оператора симметрии относительно координатной плоскости в R3.
Множество всех собственных векторов оператора , соответствующих одному собственному значению λ, если присоединить к нему нулевой вектор 0, является линейным подпространством, которое называется собственным подпространством оператора и обозначается Vλ.
Описать собственные подпространства оператора симметрии относительно координатной плоскости в R3.
Доказать, что собственные векторы линейного оператора, соответствующие различным собственным значениям, линейно независимы.
Доказательство. ( Методом математической индукции).
Пусть k − число собственных векторов в системе. При k = 1 собственный вектор один x1 0. Следовательно, x1 − линейно независимая система из одного вектора. Пусть для системы из k векторов утверждение теоремы верно. Выведем из этого предположения, что теорема верна для системы из k + 1 собственного вектора. Пусть даны собственные векторы x1, x2, …, xk, xk+1 с различными собственными значениями λ1, λ2, …, λk, λk+1 и пусть выполняется соотношение
1x1 + 2x2 + … + kxk + k+1xk+1 = 0. (1)
Для проверки линейной независимости системы требуется доказать, что все i = 0. Из (1) следует, что (1x1 + 2x2 + … + kxk + k+1xk+1) =( 0)=0. Из линейности оператора получаем 1(x1) + 2(x2) + … + k(xk) + k+1(xk+1) = 0;
1λ1x1 + 2λ2x2 + … + kλkxk + k+1λk+1xk+1 = 0. (2)
Умножим обе части равенства (1) на λk+1:
1λk+1x1 + 2λk+1x2 + … + kλk+1xk + k+1λk+1xk+1 = 0. (3)
Вычитаем из равенства (3) равенство (2):
1(λk+1 − λ1)x1 + 2(λk+1 − λ2)x2 + … + k(λk+1 − λk)xk = 0.
Так как x1, x2, …, xk − система kсобственных векторов с различными собственными значениями λ1, λ2, …, λk, то по предположению индукции все коэффициенты в последнем равенстве равны нулю, т.е. при i = 1, 2, …, k выполняются соотношения i(λk+1 − λi) = 0, но тогда i= 0, ибо λk+1 λi.
Подставив эти i= 0 в равенство (1), получаем k+1xk+1 = 0. Так как xk+1 − собственный вектор и, следовательно, ненулевой, то k+1 = 0. Теорема доказана.
5.Дать определения характеристического многочлена матрицы, спектра матрицы. Найти характеристический многочлен и спектр матрицы оператора поворота на угол α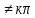 в пространстве R2. в пространстве R2.
Многочлен P (λ)= det (A − λE) называется характеристическим многочленом матрицы A. (λ)= det (A − λE) называется характеристическим многочленом матрицы A.
Доп инфа
Так как собственные векторы существуют только для тех λ, для которых det (A − λE) = 0, то собственные значения линейного оператора являются теми корнями уравнения P (λ) = 0, называемого характеристическим уравнением матрицы A, которые принадлежат полю P (R или C). Пусть λ1, λ2, …, λs − все корни характеристического уравнения (в случае поля R мы рассматриваем и комплексные корни!), k1, k2, …, ks − их кратности. (λ) = 0, называемого характеристическим уравнением матрицы A, которые принадлежат полю P (R или C). Пусть λ1, λ2, …, λs − все корни характеристического уравнения (в случае поля R мы рассматриваем и комплексные корни!), k1, k2, …, ks − их кратности.
Множество S = { , ,  , …, , …,  } называется спектром матрицы A. } называется спектром матрицы A.
Доп инфа
Спектр матрицы A − спектр ее характеристического многочлена, то есть множество корней характеристического уравнения с указанием их кратностей. Заметим, что k1 + k2 + … + ks = n.
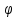 − оператор поворота на угол в R2, kπ; − оператор поворота на угол в R2, kπ;
A =  − матрица в базисе i, j; − матрица в базисе i, j;
Характеристический многочлен матрицы P (λ) = det (λ) = det  = (cos − λ)2 + sin2 = cos2 − 2λcos + λ2 + sin2 = λ2 − 2λcos + 1. Характеристическое уравнение λ2 − 2λcos + 1=0 – квадратное его дискриминант D = 4cos2 − 4 = 4(cos2 − 1) < 0. Следовательно у характеристического уравнения вещественных корней нет, а, следовательно, нет и собственных векторов. Найдем спектр матрицы поворота A .Корни характеристического уравнения- комплексно сопряженные числа λ1 = cos+isinα , λ2 = cos-isinα .S = {eiα[1], e-iα[1]} − спектр матрицы A. = (cos − λ)2 + sin2 = cos2 − 2λcos + λ2 + sin2 = λ2 − 2λcos + 1. Характеристическое уравнение λ2 − 2λcos + 1=0 – квадратное его дискриминант D = 4cos2 − 4 = 4(cos2 − 1) < 0. Следовательно у характеристического уравнения вещественных корней нет, а, следовательно, нет и собственных векторов. Найдем спектр матрицы поворота A .Корни характеристического уравнения- комплексно сопряженные числа λ1 = cos+isinα , λ2 = cos-isinα .S = {eiα[1], e-iα[1]} − спектр матрицы A.
Доп инфа
Отсутствие собственных векторов у оператора поворота вытекает также и из геометрического смысла собственного вектора. Вектор x собственный, если его образ (x) ему коллинеарен. При повороте на угол kπ (x) не коллинеарен x, если x 0.
6. Доказать, что вещественные корни характеристического многочлена матрицы линейного оператора, действующего в линейном пространстве над полем R ( и только они) являются собственными значениями этого оператора.
7. Доказать, что все корни характеристического многочлена матрицы линейного оператора, действующего в линейном пространстве над полем С ( и только они) являются собственными значениями этого оператора.
8.Изложить метод (алгоритм) нахождения собственных векторов линейного оператора.
1. Составляем матрицу A– λE
2. Вычисляем ее определитель
Пример:
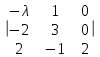 = (2 − λ)(λ2 − 3λ + 2) = −(λ − 2)2(λ − 1). (Мы разложили определитель по третьему столбцу.) = (2 − λ)(λ2 − 3λ + 2) = −(λ − 2)2(λ − 1). (Мы разложили определитель по третьему столбцу.)
У нас два собственных значения, одно из которых двукратно, и спектр таков: S = {1[1], 2[2]}.
3. Для каждого собственного значения ищем соответствующие собственные векторы
Пример (не относится к предыдущему):
Для λ1 = −1 вычисляем матрицу A ─ λ1E = A + E = 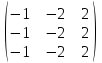 .Для нахождения собственных векторов мы должны решить однородную систему линейных уравнений с найденной матрицей. Для этого приводим матрицу к главному ступенчатому виду: .Для нахождения собственных векторов мы должны решить однородную систему линейных уравнений с найденной матрицей. Для этого приводим матрицу к главному ступенчатому виду:
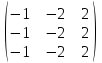 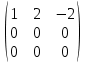 . Такой матрице соответствует система из одного уравнения: x1 + 2x2 ─ 2x3 = 0. Неизвестные x2 и x3 являются свободными, следовательно, подпространство решений двумерно. . Такой матрице соответствует система из одного уравнения: x1 + 2x2 ─ 2x3 = 0. Неизвестные x2 и x3 являются свободными, следовательно, подпространство решений двумерно.
Окончательно множество всех собственных векторов х= с собственным значением −1 можно описать в виде следующей формулы: с собственным значением −1 можно описать в виде следующей формулы:
х= =α =α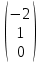 + β + β , α2 + β2 ≠ 0, а собственное подпространство V-1- линейная оболочка векторов , α2 + β2 ≠ 0, а собственное подпространство V-1- линейная оболочка векторов 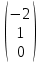 , ,
9.Доказать, что матрица оператора в базисе из собственных векторов диагональная.
10. Дать определение матрицы перехода из одного базиса в другой. Привести пример. Записать формулы преобразования координат вектора при переходе от одного базиса к другому
Матрица P = 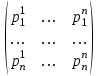 , в столбцах которой стоят координаты векторов второго базиса в первом базисе называется матрицей перехода от базиса e1, …,en к базису f1, …,fn. , в столбцах которой стоят координаты векторов второго базиса в первом базисе называется матрицей перехода от базиса e1, …,en к базису f1, …,fn.
Доп инфа
Столбцы матрицы P − векторы f1, …,fn, которые являются линейно независимыми, т.к. образуют базис. Следовательно, rk P= n, det P 0 и существует обратная матрица P−1.
Пусть собственные векторы это 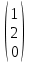 , , 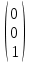 , , . .
Матрица перехода к такому базису:
T= 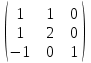 . .
Рассмотрим произвольный вектор x пространства V и разложим его по базисам e1, …,en и f1, …,fn:
x = 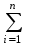 xiei = xiei = 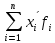
Если P = (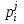 ) − матрица перехода от первого базиса ко второму, то ) − матрица перехода от первого базиса ко второму, то
fi = 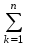 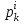 ek; ek;
x =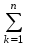 xkek = xkek =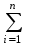 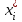 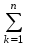 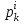 ek = ek =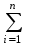 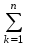 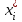 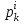 ek = ek =
=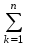 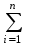 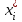 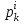 ek = ek =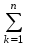 ( (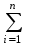 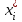 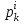 )ek. )ek.
Так как координаты вектора в данном базисе определены однозначно, то
x1 = 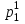 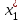 + + 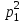 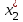 + … + + … + 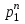 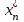 ; ;
x2 = 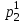 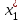 + + 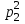 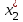 + … + + … + 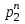 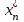 ; ;
…
xn = 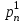 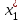 + + 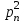 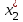 + … + + … + 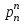 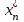 . .
В матричном виде эти соотношения записываются как
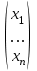 = P = P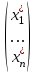 ; (4) ; (4)
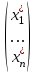 = P−1 = P−1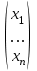 . (5) . (5)
Формулы (4) и (5) называются формулами преобразования координат векторапри переходе от одного базиса к другому.
11.Дать определение подобных матриц. Доказать, что матрицы одного оператора в разных базисах подобны.
Две матрицы A и B называются подобными (A B), если существует невырожденная матрица P такая, что B = P−1AP.
Это определение задает отношение на множестве квадратных матриц порядка n.
Матрица A этого оператора в стандартном базисе совпадает с матрицей A. (См. §2.) Рассмотрим столбцы матрицы P. Это n векторов, записанных в координатном виде в стандартном базисе, причем эти n векторов линейно независимы, так как существует P−1. Рассмотрим новый базис p1, p2, …, pn, составленный из столбцов матрицы P. Матрица перехода от стандартного базиса к базису p1, p2, …, pn совпадает с матрицей P, и, следовательно, по формуле (6) 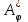 = = P−1AP = P−1AP = B, то есть подобные матрицы суть матрицы одного оператора в различных базисах. Итак, имеется взаимно однозначное соответствие между линейными операторами, действующими в пространстве V (dim V = n), и классами подобных матриц порядка n. Можно сказать, что множество всех линейных операторов является фактор множеством множества матриц порядка n по отношению подобия. = = P−1AP = P−1AP = B, то есть подобные матрицы суть матрицы одного оператора в различных базисах. Итак, имеется взаимно однозначное соответствие между линейными операторами, действующими в пространстве V (dim V = n), и классами подобных матриц порядка n. Можно сказать, что множество всех линейных операторов является фактор множеством множества матриц порядка n по отношению подобия.
Определим некоторые инварианты подобных матриц.
12. Доказать, что характеристические многочлены и ранги подобных матриц равны.
Характеристические многочлены подобных матриц равны.
Доказательство. Обозначим характеристические многочлены: PA(λ) = det (A − λE), PB(λ) = det (B − λE); нам дано, что A
B, т.е. B = C−1AC. Имеем: PB(λ) = det (B − λE) = det (C−1AC − C−1(λE)C) = det (C−1(A − λE)C) = det C−1det (A − λE)det C = det (A − λE) = PA(λ).
Таким образом коэффициенты характеристического многочлена являются инвариантами .
Следствие. Спектры подобных матриц совпадают.
Из этой теоремы следует, что можно ввести понятия характеристического многочлена Pφ (λ) оператора , спектра Sφ оператора , вычисляя их по матрице A, взятой в произвольном базисе пространства V.
Важной геометрической характеристикой линейного оператора является размерность пространства Im . Если A - матрица оператора в некотором базисе, то dim Im =rk A и , следовательно, ранги подобных матриц совпадают.
13. Дать определение диагонализируемого оператора. Доказать, что оператор диагонализируем, если его характеристический многочлен P (λ) имеет n различных корней в поле P. (λ) имеет n различных корней в поле P.
Определение. Оператор называется диагонализируемым, если существует базис, в котором его матрица диагональна.
Если A − матрица такого оператора в произвольном базисе, то она подобна матрице D =  , A D. , A D.
Как же по матрице A узнать, диагонализируем ли оператор ? Мы уже знаем, что в некоторых случаях, а именно, если спектр оператора Sφ = {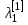 , , 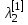 , …, , …, 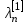 },и все корни характеристического уравнения лежат в рассматриваемом поле, то оператор диагонализируем. },и все корни характеристического уравнения лежат в рассматриваемом поле, то оператор диагонализируем.
Если оператор диагонализируем, а характеристические многочлены подобных матриц равны ( теорема 4), то
Pφ (λ) = PD(λ) = det 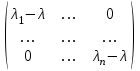 = (−1)n(λ − λ1)…( λ − λn). (7) = (−1)n(λ − λ1)…( λ − λn). (7)
Мы видим, что характеристический многочлен диагонализируемого оператора разлагается на линейные множители в рассматриваемом поле,
причем в последнем выражении возможно повторение сомножителей. Для поля C это условие, как известно, выполняется всегда. Для поля R оно означает, что все корни характеристического многочлена являются действительными числами, причем равными тем самым λi, которые стоят на диагонали матрицы D. Заметим, однако, что условие принадлежности всех корней характеристического уравнения рассматриваемому полю еще не является достаточным для диагонализируемости оператора. Рассмотрим, например, матрицу порядка n:
Jn () = 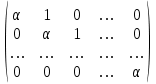 , (8) , (8)
называемую жордановой клеткой, и оператор умножения на эту матрицу в пространстве Rn. Характеристический многочлен
P () = 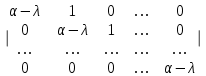 = ( )n, = ( )n,
имеет один корень кратности n, и, следовательно, спектр оператора имеет вид S = {[n]}. Если бы матрица Jn () была подобна диагональной матрице D, то ее вид должен был бы быть:
D = 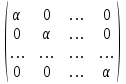 , ,
так как спектры подобных матриц совпадают, и, следовательно, оператор был бы гомотетией с коэффициентом , что неверно, так как умножение на матрицу Jn () переводит вектор x =  в вектор в вектор
y = Jn () = = 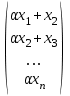  . .
14.Сформулировать ( доказать) теорему о диагонализируемом операторе. Привести пример .
Теорема 5. Оператор диагонализируем тогда и только тогда, когда выполняются два условия.
1. Характеристический многочлен разлагается на линейные множители в рассматриваемом поле.
2. Размерность каждого собственного подпространства равна кратности соответствующего корня характеристического многочлена.
Доказательство.
Необходимость. Пусть оператор - диагонализируем, и пусть e1, …,en – базис, в котором A = D, тогда этот базис состоит из собственных векторов оператора . Действительно, пусть e1, …,en – базис, в котором A = D; тогда векторы можно записать в координатном виде : ei = 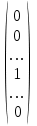 (1 на i-м месте) и найти их образы φ(ei) = (1 на i-м месте) и найти их образы φ(ei) = 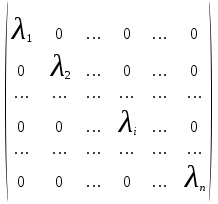 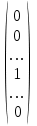 = = 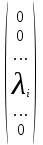 = λi ei. = λi ei.
Таким образом, числа, стоящие на диагонали матрицы D- собственные значения оператора . Формулу (7) можно записать в виде: , Pφ (λ)=
(−1)n(λ − λ1)к1…( λ – λs)ks, где λ1...λs- различные числа, стоящие на диагонали матрицы D. Они являются корнями характеристического многочлена, а k1,…ks-кратности соответствующих корней. Найдем размерности собственных подпространств Vλi . Собственное подпространство Vλi -подпространство решений однородной системы с матрицей A-λiE, следовательно размерность подпространства dim Vλi = n-rk( A-λiE). В случае A = D, матрица D- λiE – диагональная, причем на месте λi на диагонале стоят 0, а остальные диагональные элементы имеют вид λj - λi и отличны от нуля. Ранг такой матрицы равен числу отличных от нуля элементов на диагонали( проверьте) и равен n-ki.Следовательно dim Vλi = ki.
Достаточность. Пусть характеристический многочлен оператора разлагается на линейные множители в рассматриваемом поле, Pφ (λ)=
(−1)n(λ − λ1)к1…( λ – λs)ks, где λ1...λs- различные корни характеристического многочлена, а k1,…ks-кратности соответствующих корней, причем k1+…+ks =n. Если размерности собственных подпространств Vλi = ki, то внутри каждого собственного подпространства можно найти ki линейно независимых собственных векторов e1i, …,ekii соответствующих собственному значению λi . Соберем эти векторы в систему e11, …,ek11 ,…, e1s, …,ekss . В системе k1+…+ks =n векторов. Докажем линейную независимость этой системы, для чего рассмотрим линейную комбинацию этих векторов и приравняем ее к 0.
α11 e11+ …+ αк11ek11 +…+ α1s e1s+ …+ αkssekss =0. Сгруппируем векторы следующим образом: (α11 e11+ …+ αк11ek11 ) +…+( α1s e1s+ …+ αkssekss )=0. В каждой скобке находиться вектор из собственного подпространства, следовательно ,это либо собственный вектор оператора , либо вектор 0, добавленный к собственным векторам. Но вектор в скобке не может быть ненулевым, ибо в противном случае мы получим нетривиальную линейную комбинацию собственных векторов оператора , отвечающих различным собственным значениям равную 0. Но это невозможно, так как согласно теореме 2, такие векторы линейно независимы. Итак, в каждой скобке должен быть нулевой вектор. Но линейная комбинация базисных векторов равно 0 только, если все коэффициенты αij равны нулю. Из этого следует, что система e11, …,ek11 ,…, e1s, …,ekss линейно независима и образует базис линейного пространства. Этот базис состоит из собственных векторов, матрица оператора в котором – диагональная.
Пример. Рассмотрим снова оператор умножения на жорданову клетку (8) и найдем собственные векторы этого оператора . Единственное собственное значение оператора − число . Собственное подпространство находим из решения системы (3) §8. В рассматриваемом случае система принимает вид: 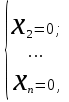 , в которой x1 − свободное неизвестное. Пространство V = , в которой x1 − свободное неизвестное. Пространство V =  , dim V = 1, и собственных векторов не хватает, чтобы составить из них базис пространства Rn. Второе условие теоремы о диагонализируемости оператора не выполняется, т. к. кратность корня равна n, а dim V = 1 (мы предполагаем, что n > 1). , dim V = 1, и собственных векторов не хватает, чтобы составить из них базис пространства Rn. Второе условие теоремы о диагонализируемости оператора не выполняется, т. к. кратность корня равна n, а dim V = 1 (мы предполагаем, что n > 1).
Рассмотрим конкретные примеры на применение изложенных методов.
Дана матрица A = 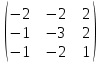 , и известно, что она в стандартном , и известно, что она в стандартном
базисе является матрицею некоторого линейного оператора , действующего в пространстве R3: A = A. Найдем собственные числа и собственные векторы оператора .
Составляем матрицу A– λE= 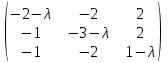 и вычисляем ее определитель, то есть характеристический многочлен оператора , разложением по третьему столбцу ( можно вычислять любым удобным способом) и вычисляем ее определитель, то есть характеристический многочлен оператора , разложением по третьему столбцу ( можно вычислять любым удобным способом)
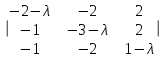 = 2 = 2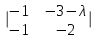 − 2 − 2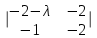 + (1 − λ) + (1 − λ) 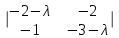 = 2(2 − 3 − λ) − 2(4 + 2λ − 2) + (1 − λ)(6 + 5λ + λ2 − 2) = 2(−1 − λ) − 2(2λ + 2) + (1 − λ)(λ2 + 5λ + 4) = −2 − − 2λ − 4λ − 4 + λ2 + 5λ + 4 − λ3 − 5λ2 − 4λ = −λ3 − 4λ2 − 5λ − 2. = 2(2 − 3 − λ) − 2(4 + 2λ − 2) + (1 − λ)(6 + 5λ + λ2 − 2) = 2(−1 − λ) − 2(2λ + 2) + (1 − λ)(λ2 + 5λ + 4) = −2 − − 2λ − 4λ − 4 + λ2 + 5λ + 4 − λ3 − 5λ2 − 4λ = −λ3 − 4λ2 − 5λ − 2.
Собственные числа нашего оператора суть вещественные корни этого многочлена. Решим характеристическое уравнение −λ3 − 4λ2 − 5λ − 2 = 0.
В надежде отыскать целый корень этого уравнения испытаем делители свободного члена. Немедленно обнаруживаем, что, например, число −1 является корнем. Для нахождения остальных корней воспользуемся теоремой Безу и разделим наш многочлен на λ + 1, получаем в частном многочлен − λ2 − 3λ − 2, а это уже квадратный трехчлен, корни которого: −1 и −2. Имеем разложение: − λ2 − 3λ − 2 = −(λ + 1)(λ + 2), а характеристический многочлен разлагается на линейные множители PA(λ) = −λ3 − 4λ2 − 5λ − 2 = −(λ + 1)2(λ + 2).
Таким образом, у нас два собственных значения, одно из которых двукратно, и спектр таков: S = {(−1)[2], (−2)[1]}. Теперь для каждого собственного значения надо найти соответствующие собственные векторы. Для λ1 = −1 вычисляем матрицу A ─ λ1E = A + E = 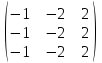 .Для нахождения собственных векторов мы должны решить однородную систему линейных уравнений с найденной матрицей. Для этого приводим матрицу к главному ступенчатому виду: .Для нахождения собственных векторов мы должны решить однородную систему линейных уравнений с найденной матрицей. Для этого приводим матрицу к главному ступенчатому виду:
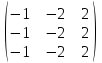 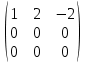 . Такой матрице соответствует система из одного уравнения: x1 + 2x2 ─ 2x3 = 0. Неизвестные x2 и x3 являются свободными, следовательно, подпространство решений двумерно. . Такой матрице соответствует система из одного уравнения: x1 + 2x2 ─ 2x3 = 0. Неизвестные x2 и x3 являются свободными, следовательно, подпространство решений двумерно.
Окончательно множество всех собственных векторов х= с собственным значением −1 можно описать в виде следующей формулы: с собственным значением −1 можно описать в виде следующей формулы:
х= =α =α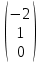 + β + β , α2 + β2 ≠ 0, а собственное подпространство V-1- линейная оболочка векторов , α2 + β2 ≠ 0, а собственное подпространство V-1- линейная оболочка векторов 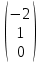 , , . .
А теперь тем же методом найдем собственные векторы, соответствующие собственному значению −2.
Вычисляем матрицу A ─ λ2E = A + 2E = 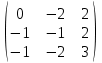 и приводим ее к главному ступенчатому виду: и приводим ее к главному ступенчатому виду: 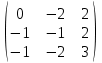 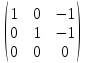 . .
Соответствующая система состоит из двух уравнений: 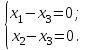
Теперь свободное неизвестное - x3, и подпространство решений одномерно.
Множество всех собственных векторов с собственным значением −2 можно описать в виде формулы:
х= =α =α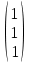 , α ≠ 0, собственное подпространство V-2 порождается вектором , α ≠ 0, собственное подпространство V-2 порождается вектором 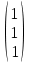 . .
Мы видим, что у нас выполняются все условия теоремы, так что должен существовать базис из собственных векторов. Для нахождения такого базиса достаточно объединить найденные нами базисы в подпространствах решений двух однородных систем. Матрица перехода к такому базису есть матрица, столбцы которой суть найденные базисные векторы: Р= 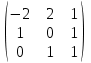 . .
Матрица нашего линейного оператора в этом новом базисе будет диагональной: A’ = 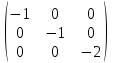 . .
Осталось проверить выполнение формулы (6): P−1AP =  . Вместо этой формулы удобнее, однако, проверять эквивалентную ей формулу: . Вместо этой формулы удобнее, однако, проверять эквивалентную ей формулу:
AР = РA’.
Вычисляя обе части этой формулы, имеем: AР =РA’ = 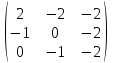 . .
15.Рассмотреть пример не диагонализируемого оператора ( оператора умножения на жорданову клетку). |
 Скачать 128.32 Kb.
Скачать 128.32 Kb.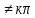 в пространстве R2.
в пространстве R2. 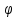 − оператор поворота на угол в R2, kπ;
− оператор поворота на угол в R2, kπ;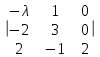 = (2 − λ)(λ2 − 3λ + 2) = −(λ − 2)2(λ − 1). (Мы разложили определитель по третьему столбцу.)
= (2 − λ)(λ2 − 3λ + 2) = −(λ − 2)2(λ − 1). (Мы разложили определитель по третьему столбцу.)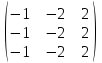 .Для нахождения собственных векторов мы должны решить однородную систему линейных уравнений с найденной матрицей. Для этого приводим матрицу к главному ступенчатому виду:
.Для нахождения собственных векторов мы должны решить однородную систему линейных уравнений с найденной матрицей. Для этого приводим матрицу к главному ступенчатому виду: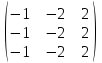
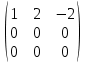 . Такой матрице соответствует система из одного уравнения: x1 + 2x2 ─ 2x3 = 0. Неизвестные x2 и x3 являются свободными, следовательно, подпространство решений двумерно.
. Такой матрице соответствует система из одного уравнения: x1 + 2x2 ─ 2x3 = 0. Неизвестные x2 и x3 являются свободными, следовательно, подпространство решений двумерно.  с собственным значением −1 можно описать в виде следующей формулы:
с собственным значением −1 можно описать в виде следующей формулы: =α
=α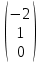 + β
+ β , α2 + β2 ≠ 0, а собственное подпространство V-1- линейная оболочка векторов
, α2 + β2 ≠ 0, а собственное подпространство V-1- линейная оболочка векторов 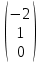 ,
,
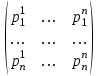 , в столбцах которой стоят координаты векторов второго базиса в первом базисе называется матрицей перехода от базиса e1, …,en к базису f1, …,fn.
, в столбцах которой стоят координаты векторов второго базиса в первом базисе называется матрицей перехода от базиса e1, …,en к базису f1, …,fn. 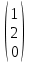 ,
, 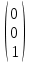 ,
, .
.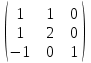 .
.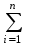 xiei =
xiei = 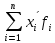
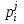 ) − матрица перехода от первого базиса ко второму, то
) − матрица перехода от первого базиса ко второму, то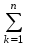
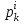 ek;
ek; 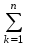 xkek =
xkek =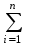
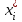
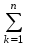
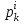 ek =
ek =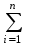
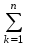
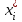
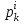 ek =
ek =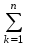
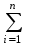
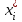
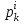 ek =
ek =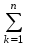 (
(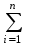
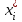
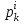 )ek.
)ek.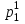
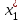 +
+ 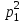
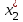 + … +
+ … + 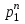
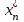 ;
;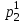
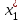 +
+ 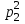
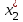 + … +
+ … + 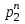
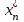 ;
;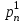
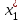 +
+ 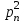
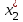 + … +
+ … + 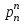
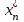 .
.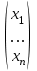 = P
= P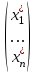 ; (4)
; (4)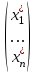 = P−1
= P−1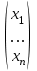 . (5)
. (5)
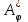 = = P−1AP = P−1AP = B, то есть подобные матрицы суть матрицы одного оператора в различных базисах. Итак, имеется взаимно однозначное соответствие между линейными операторами, действующими в пространстве V (dim V = n), и классами подобных матриц порядка n. Можно сказать, что множество всех линейных операторов является фактор множеством множества матриц порядка n по отношению подобия.
= = P−1AP = P−1AP = B, то есть подобные матрицы суть матрицы одного оператора в различных базисах. Итак, имеется взаимно однозначное соответствие между линейными операторами, действующими в пространстве V (dim V = n), и классами подобных матриц порядка n. Можно сказать, что множество всех линейных операторов является фактор множеством множества матриц порядка n по отношению подобия. 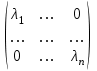 , A D.
, A D. ,
,  , …,
, …, 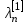 },и все корни характеристического уравнения лежат в рассматриваемом поле, то оператор диагонализируем.
},и все корни характеристического уравнения лежат в рассматриваемом поле, то оператор диагонализируем. 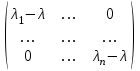 = (−1)n(λ − λ1)…( λ − λn). (7)
= (−1)n(λ − λ1)…( λ − λn). (7)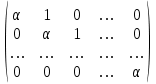 , (8)
, (8)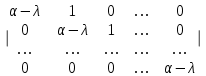 = ( )n,
= ( )n,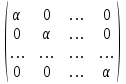 ,
, в вектор
в вектор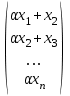
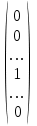 (1 на i-м месте) и найти их образы φ(ei) =
(1 на i-м месте) и найти их образы φ(ei) = 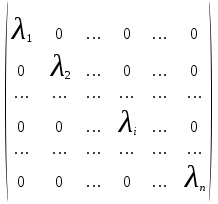
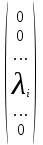 = λi ei.
= λi ei.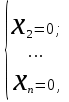 , в которой x1 − свободное неизвестное. Пространство V =
, в которой x1 − свободное неизвестное. Пространство V =  , dim V = 1, и собственных векторов не хватает, чтобы составить из них базис пространства Rn. Второе условие теоремы о диагонализируемости оператора не выполняется, т. к. кратность корня равна n, а dim V = 1 (мы предполагаем, что n > 1).
, dim V = 1, и собственных векторов не хватает, чтобы составить из них базис пространства Rn. Второе условие теоремы о диагонализируемости оператора не выполняется, т. к. кратность корня равна n, а dim V = 1 (мы предполагаем, что n > 1).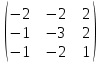 , и известно, что она в стандартном
, и известно, что она в стандартном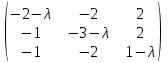 и вычисляем ее определитель, то есть характеристический многочлен оператора , разложением по третьему столбцу ( можно вычислять любым удобным способом)
и вычисляем ее определитель, то есть характеристический многочлен оператора , разложением по третьему столбцу ( можно вычислять любым удобным способом) 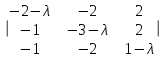 = 2
= 2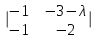 − 2
− 2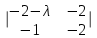 + (1 − λ)
+ (1 − λ) 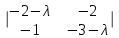 = 2(2 − 3 − λ) − 2(4 + 2λ − 2) + (1 − λ)(6 + 5λ + λ2 − 2) = 2(−1 − λ) − 2(2λ + 2) + (1 − λ)(λ2 + 5λ + 4) = −2 − − 2λ − 4λ − 4 + λ2 + 5λ + 4 − λ3 − 5λ2 − 4λ = −λ3 − 4λ2 − 5λ − 2.
= 2(2 − 3 − λ) − 2(4 + 2λ − 2) + (1 − λ)(6 + 5λ + λ2 − 2) = 2(−1 − λ) − 2(2λ + 2) + (1 − λ)(λ2 + 5λ + 4) = −2 − − 2λ − 4λ − 4 + λ2 + 5λ + 4 − λ3 − 5λ2 − 4λ = −λ3 − 4λ2 − 5λ − 2. 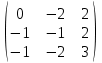 и приводим ее к главному ступенчатому виду:
и приводим ее к главному ступенчатому виду: 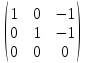 .
.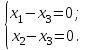
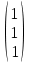 , α ≠ 0, собственное подпространство V-2 порождается вектором
, α ≠ 0, собственное подпространство V-2 порождается вектором 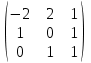 .
.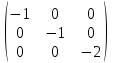 .
.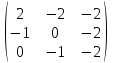 .
.