Практикум по теме Первый и второй замечательные пределы. Первый замечательный предел
 Скачать 127.09 Kb.
|
|
Первый замечательный предел Рассмотрим следующий предел:  (вместо родной буквы «хэ» я буду использовать греческую букву «альфа», это удобнее с точки зрения подачи материала).Согласно нашему правилу нахождения пределов пробуем подставить ноль в функцию: в числителе у нас получается ноль (синус нуля равен нулю), в знаменателе, очевидно, тоже ноль. Таким образом, мы сталкиваемся с неопределенностью вида  , которую, к счастью, раскрывать не нужно. В курсе математического анализа, доказывается, что: Данный математический факт носит название Первого замечательного предела. Нередко в практических заданиях функции могут быть расположены по-другому, это ничего не меняет:  – тот же самый первый замечательный предел.! Но самостоятельно переставлять числитель и знаменатель нельзя! Если дан предел в виде  , то и решать его нужно в таком же виде, ничего не переставляя.На практике в качестве параметра  может вы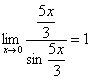ступать не только переменная  , но и элементарная функция, сложная функция. Важно лишь, чтобы она стремилась к нулю.Примеры:  ,  ,  ,  Здесь  ,  ,  ,  , и всё хорошо– первый замечательный предел применим.А вот следующая запись – неправильна: 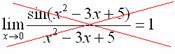 Почему? Потому что многочлен  не стремится к нулю, он стремится к пятерке.На практике не все так гладко, почти никогда студенту не предложат решить простой предел  и получить лёгкий зачет. Переходим к рассмотрению практических примеров: Пример 1 Найти предел  Если мы замечаем в пределе синус, то это нас сразу должно наталкивать на мысль о возможности применения первого замечательного предела. Сначала пробуем подставить 0 в выражение под знак предела (делаем это мысленно или на черновике):  Итак, у нас есть неопределенность вида , ее обязательно указываем в оформлении решения. Выражение под знаком предела у нас похоже на первый замечательный предел, но это не совсем он, под синусом находится  , а в знаменателе  .В подобных случаях первый замечательный предел нам нужно организовать самостоятельно, используя искусственный прием. Ход рассуждений может быть таким: «под синусом у нас , значит, в знаменателе нам тоже нужно получить ».А делается это очень просто: 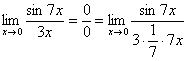 То есть, знаменатель искусственно умножается в данном случае на 7 и делится на ту же семерку. Теперь запись у нас приняла знакомые очертания. Когда задание оформляется от руки, то первый замечательный предел желательно пометить простым карандашом: 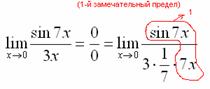 Что произошло? По сути, обведенное выражение у нас превратилось в единицу и исчезло в произведении: 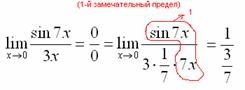 Теперь только осталось избавиться от трехэтажной дроби: 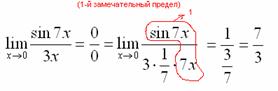 Готово. Окончательный ответ:  Если не хочется использовать пометки карандашом, то решение можно оформить так: “  Используем первый замечательный предел 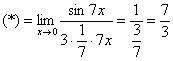 “ Пример 2 Найти предел 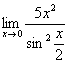 Опять мы видим в пределе дробь и синус. Пробуем подставить в числитель и знаменатель ноль: 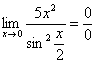 Действительно, у нас неопределенность 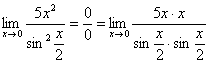и, значит, нужно попытаться организовать первый замечательный предел. Раньше мы рассматривали правило, что когда у нас есть неопределенность , то нужно разложить числитель и знаменатель на множители. Здесь – то же самое, степени мы представим в виде произведения (множителей): Далее, по уже знакомой схеме организовываем первые замечательные пределы. Под синусами у нас 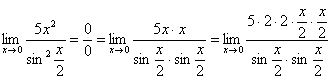 , значит, в числителе тоже нужно получить : Аналогично предыдущему примеру, обводим карандашом замечательные пределы (здесь их два), и указываем, что они стремятся к единице: 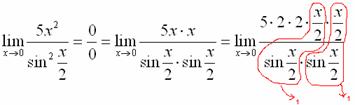 Собственно, ответ готов: 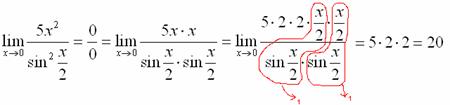 Пример 3 Найти предел  Подставляем ноль в выражение под знаком предела:  Получена неопределенность , которую нужно раскрывать. Если в пределе есть тангенс, то почти всегда его превращают в синус и косинус по известной тригонометрической формуле  (кстати, с котангенсом делают примерно то же самое, см. тригонометрические формулы ).В данном случае:  Косинус нуля равен единице, и от него легко избавиться (не забываем пометить, что он стремится к единице):  Таким образом, если в пределе косинус является МНОЖИТЕЛЕМ, то его, грубо говоря, нужно превратить в единицу, которая исчезает в произведении. Дальше по накатанной схеме, организуем первый замечательный предел: 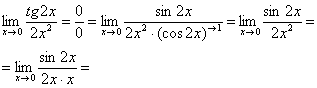 Здесь все вышло проще, без всяких домножений и делений. Первый замечательный предел тоже превращается в единицу и исчезает в произведении: 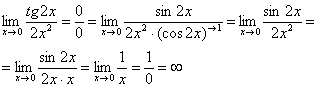 В итоге получена бесконечность, бывает и такое. Пример 4 Найти предел  Пробуем подставить ноль в числитель и знаменатель:  Получена неопределенность (косинус нуля, как мы помним, равен единице)Используем тригонометрическую формулу  . Возьмите на заметку! Пределы с применением этой формулы почему-то встречаются очень часто. Постоянные множители вынесем за значок предела:  Организуем первый замечательный предел: 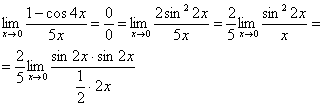 Здесь у нас только один замечательный предел, который превращается в единицу и исчезает в произведении: 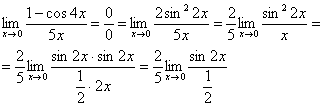 Избавимся от трехэтажности: 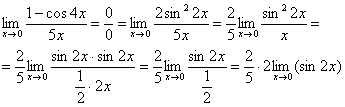 Предел фактически решен, указываем, что оставшийся синус стремится к нулю: 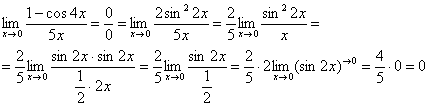 Пример 5 Найти предел  Этот пример сложнее, попробуйте разобраться самостоятельно: 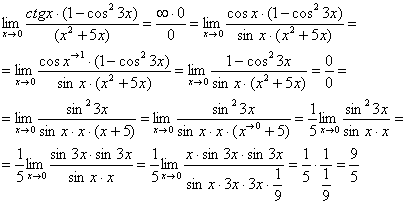 Второй замечательный предел В теории математического анализа доказано, что:  Данный факт носит название второго замечательного предела. Справка:  – это иррациональное число.В качестве параметра может выступать не только переменная , но и сложная функция. Важно лишь, чтобы она стремилась к бесконечности.Пример 6 Найти предел  Когда выражение под знаком предела находится в степени – это первый признак того, что нужно попытаться применить второй замечательный предел. Но сначала, как всегда, пробуем подставить бесконечно большое число в выражение  .Нетрудно заметить, что при  основание степени  , а показатель –  , то есть имеется, неопределенность вида  : Данная неопределенность как раз и раскрывается с помощью второго замечательного предела. Но, как часто бывает, второй замечательный предел не лежит на блюдечке с голубой каемочкой, и его нужно искусственно организовать. Рассуждать можно следующим образом: в данном примере параметр 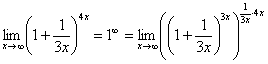 , значит, в показателе нам тоже нужно организовать . Для этого возводим основание в степень , и, чтобы выражение не изменилось – возводим в степень  : Когда задание оформляется от руки, карандашом помечаем: 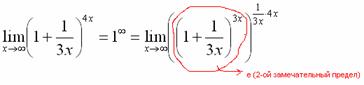 Практически всё готово, страшная степень превратилась в симпатичную букву  :При этом сам значок предела перемещаем в показатель: 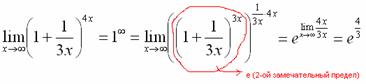 Далее, отметки карандашом я не делаю, принцип оформления, думаю, понятен. Пример 7 Найти предел  Внимание! Предел подобного типа встречается очень часто, пожалуйста, очень внимательно изучите данный пример. Пробуем подставить бесконечно большое число в выражение, стоящее под знаком предела:  В результате получена неопределенность  . Но второй замечательный предел применим к неопределенности вида . Что делать? Нужно преобразовать основание степени. Рассуждаем так: в знаменателе у нас  , значит, в числителе тоже нужно организовать : Теперь можно почленно разделить числитель на знаменатель:  Вроде бы основание стало напоминать 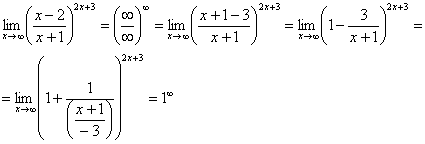 , но у нас знак «минус» да и тройка какая-то вместо единицы. Поможет следующее ухищрение, делаем дробь трехэтажной: Таким образом, основание приняло вид , и, более того, появилась нужная нам неопределенность . Организуем второй замечательный предел  .Легко заметить, что в данном примере 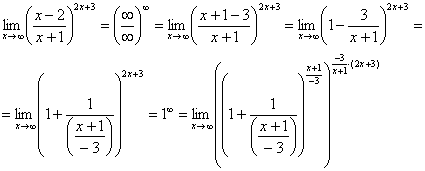 . Снова исполняем наш искусственный прием: возводим основание степени в  , и, чтобы выражение не изменилось – возводим в обратную дробь  : Наконец-то долгожданное 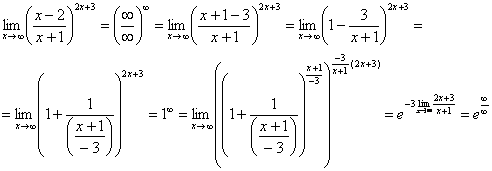 устроено, с чистой совестью превращаем его в букву : Но на этом мучения не закончены, в показателе у нас появилась неопределенность вида  . Делим числитель и знаменатель на : Готово. А сейчас мы рассмотрим модификацию второго замечательного предела. Напомню, что второй замечательный предел выглядит следующим образом: . Однако на практике время от времени можно встретить его «перевёртыш», который в общем виде записывается так: Пример 8 Найти предел  Сначала (мысленно или на черновике) пробуем подставить ноль (бесконечно малое число) в выражение, стоящее под знаком предела:  В результате получена знакомая неопределенность 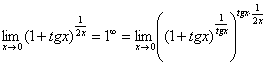. Очевидно, что в данном примере  . С помощью знакомого искусственного приема организуем в показателе степени конструкцию  : Выражение 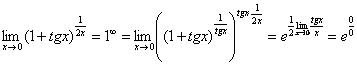 со спокойной душой превращаем в букву : Еще не всё, в показателе у нас появилась неопределенность вида 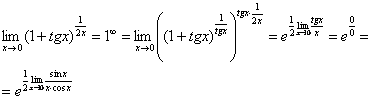 . Раскладываем тангенс на синус и косинус (ничего не напоминает?): Косинус нуля стремится к единице (не забываем помечать карандашом), поэтому он просто пропадает в произведении:  А что такое и к чему оно стремится, нужно уже знать, иначе «двойка»!Как видите, в практических заданиях на вычисление пределов нередко требуется применять сразу несколько правил и приемов. |