Док. Впервые идея применения алгоритмов машинного обучения к зашифрованным данным возникла, и получила развитие,однако практически реализована только в виде программной библиотеки

Название	Впервые идея применения алгоритмов машинного обучения к зашифрованным данным возникла, и получила развитие,однако практически реализована только в виде программной библиотеки
Дата	26.05.2019
Размер	197.1 Kb.
Формат файла
Имя файла	Док.docx
Тип	Документы #78948

Введение
Впервые идея применения алгоритмов машинного обучения к зашифрованным данным возникла, и получила развитие ,однако практически реализована только в виде программной библиотеки. Классификаторы являются бесценным инструментом во многих местах ,сегодня например медицинских или геномных предсказаниях, обнаружении спама, распознавании лиц, и финансовых вычислениях. Многие из этих приложений обрабатывают конфиденциальные данные, поэтому важно чтобы данные и классификатор оставались в секрете. Рассмотрим типичную ситуацию обучения с учителем, изображенную на рисунке . Алгоритмы обучения с учителем состоят из двух фаз: (1) фазы обучения, в течение которого алгоритм строит модель �� по набору пар «объект, ответ», называемом обучающей выборкой (или прецедентами), и (2) фазы распознавания на которой классификатор �� запускается над ранее неизвестным вектором признаков ��, используя модель �� для вывода ответа-результата ��(��, ��). В приложениях, обрабатывающих конфиденциальные данные, важно, чтобы вектор признаков �� и модель �� оставались в секрете для одного или нескольких участников. Рассмотрим пример медицинского исследования или больницы, имеющей модель, построенную с по- мощью конфиденциальных медицинских данных некоторых пациентов; модель конфиденциальна, поскольку содержит информацию о пациентах, и её использование должно быть совместимым с ФЗ «О защите персональных данных»1 . Клиент хочет использовать модель, чтобы сделать прогноз о своем здоровье (например, насколько вероятно быстрое излечение, или, будет ли успешным лечение в стационаре), но не хочет раскрывать свои конфиденциальные медицинские параметры. В идеале, больница и клиент запускают протокол после 1 закон № 152-ФЗ «О персональных данных» 20 Л. К. Бабенко, Ф. Б. Буртыка, О. Б. Макаревич, А. В. Трепачева Рис. 4. Общая модель. Каждый заштрихованный квадрат указывает секретные данные, которые должны быть доступны только одному участнику: прецеденты и модель серверу, а данные и результат – клиенту. Каждый прямой без пунктирный прямоугольник указывает алгоритм, одиночные стрелки указывают входные данные алгоритма, а двойные стрелки указывают результаты. которого клиент узнает один бит («да / нет»), и ни одна из сторон не узнает что-нибудь еще о исходных данных другой. Подобная же ситуация возникает в финансовом учреждении (например, страховой компании), которая держит в секрете модель, а заказчик хочет оценить цены или качество обслуживания на основе своей личной информации.Что представляет собой машинное обучение Благодаря машинному обучению программист не обязан писать инструкции, учитывающие все возможные проблемы и содержащие все решения. Вместо этого в компьютер (или отдельную программу) закладывают алгоритм самостоятельного нахождения решений путём комплексного использования статистических данных, из которых выводятся закономерности и на основе которых делаются прогнозы. Технология машинного обучения на основе анализа данных берёт начало в 1950-х гг., когда начали разрабатывать первые программы для игры в шашки. За прошедшие десятилетия общий принцип не изменился. Зато благодаря взрывному росту вычислительных мощностей компьютеров многократно усложнились закономерности и прогнозы, создаваемые ими, и расширился круг проблем и задач, решаемых с использованием машинного обучения. 3 примера применения машинного обучения, чтобы ускорить бизнес-процессы Чтобы запустить процесс машинного обучения, для начала необходимо загрузить в компьютер некоторое количество исходных данных, на которых ему предстоит учиться обрабатывать запросы. Например, это могут быть фотографии, которым присвоены описания: «здесь есть кот» или «здесь нет кота». После этого программа уже сможет самостоятельно распознавать котов на вновь загруженных картинках. Обучение продолжается и дальше, ведь все загруженные и проанализированные – и верно, и ошибочно – изображения попадают в ту же базу данных. Поэтому, чем больше данных обработано, тем «умнее» программа и всё более точно она решает поставленную задачу. В наше время компьютеры активно применяются в тех сферах, которые всегда считались подвластными только людям. Конечно, некоторые технологии и наработки ещё только входят на рынок и далеко не идеальны, но это только начало пути. Машинное обучение, дающее возможность машинам самостоятельно совершенствовать свою работу, открывает им возможности для бесконечного развития. Благодаря машинному обучению компьютеры учатся распознавать на фотографиях и рисунках не только лица, но и пейзажи, предметы, текст и цифры. Что касается текста, то и здесь не обойтись без машинного обучения: функция проверки грамматики сейчас присутствует в любом текстовом редакторе и даже в телефонах. Причем учитывается не только написание слов, но и контекст, оттенки смысла и другие тонкие лингвистические аспекты. Более того, уже существует программное обеспечение, способное без участия человека писать новостные статьи (на тему экономики и, к примеру, спорта).Любое использование материалов допускается только при наличии гиперссылки.

Задачи машинного обучения. Все задачи, которые решаются с помощью машинного обучения, относятся к одной из следующих категорий. Задача регрессии – прогноз на основе выборки объектов с различными признаками. На выходе должно получиться вещественное число (2, 35, 76.454 и др.), к примеру цена квартиры, стоимость ценной бумаги по прошествии полугода, ожидаемый доход магазина на следующий месяц, качество вина при слепом тестировании. Задача классификации – получение категориального ответа на основе набора признаков. Имеет конечное количество ответов (как правило, в формате «да» или «нет»): есть ли на фотографии кот, является ли изображение человеческим лицом, болен ли пациент раком. Задача кластеризации – распределение данных на группы: разделение всех клиентов мобильного оператора по уровню платёжеспособности, отнесение космических объектов к той или иной категории (планета, звёзда, чёрная дыра и т. п.). Задача уменьшения размерности – сведение большого числа признаков к меньшему (обычно 2–3) для удобства их последующей визуализации (например, сжатие данных). Задача выявления аномалий – отделение аномалий от стандартных случаев. На первый взгляд она совпадает с задачей классификации, но есть одно существенное отличие: аномалии – явление редкое, и обучающих примеров, на которых можно натаскать машинно обучающуюся модель на выявление таких объектов, либо исчезающе мало, либо просто нет, поэтому методы классификации здесь не работают. На практике такой задачей является, например, выявление мошеннических действий с банковскими картами.

Основные виды машинного обучения Основная масса задач, решаемых при помощи методов машинного обучения, относится к двум разным видам: обучение с учителем (supervised learning) либо без него (unsupervised learning). Однако этим учителем вовсе не обязательно является сам программист, который стоит над компьютером и контролирует каждое действие в программе. «Учитель» в терминах машинного обучения – это само вмешательство человека в процесс обработки информации. В обоих видах обучения машине предоставляются исходные данные, которые ей предстоит проанализировать и найти закономерности. Различие лишь в том, что при обучении с учителем есть ряд гипотез, которые необходимо опровергнуть или подтвердить. Эту разницу легко понять на примерах.

Наиболее часто используемые алгоритмы машинного обучения

1. Дерево принятия решений. Это метод поддержки принятия решений, основанный на использовании древовидного графа: модели принятия решений, которая учитывает их потенциальные последствия (с расчётом вероятности наступления того или иного события), эффективность, ресурсозатратность. Для бизнес-процессов это дерево складывается из минимального числа вопросов, предполагающих однозначный ответ — «да» или «нет». Последовательно дав ответы на все эти вопросы, мы приходим к правильному выбору. Методологические преимущества дерева принятия решений – в том, что оно структурирует и систематизирует проблему, а итоговое решение принимается на основе логических выводов.

2. Наивная байесовская классификация Наивные байесовские классификаторы относятся к семейству простых вероятностных классификаторов и берут начало из теоремы Байеса, которая применительно к данному случаю рассматривает функции как независимые (это называется строгим, или наивным, предположением). На практике используется в следующих областях машинного обучения: определение спама, приходящего на электронную почту; автоматическая привязка новостных статей к тематическим рубрикам; выявление эмоциональной окраски текста; распознавание лиц и других паттернов на изображениях.

3. Метод наименьших квадратов Всем, кто хоть немного изучал статистику, знакомо понятие линейной регрессии. К вариантам её реализации относятся и наименьшие квадраты. Обычно с помощью линейной регрессии решают задачи по подгонке прямой, которая проходит через множество точек. Вот как это делается с помощью метода наименьших квадратов: провести прямую, измерить расстояние от неё до каждой из точек (точки и линию соединяют вертикальными отрезками), получившуюся сумму перенести наверх. В результате та кривая, в которой сумма расстояний будет наименьшей, и есть искомая (эта линия пройдёт через точки с нормально распределённым отклонением от истинного значения). Линейная функция обычно используется при подборе данных для машинного обучения, а метод наименьших квадратов – для сведения к минимуму погрешностей путем создания метрики ошибок.

4. Логистическая регрессия Логистическая регрессия – это способ определения зависимости между переменными, одна из которых категориально зависима, а другие независимы. Для этого применяется Логистическая функция (аккумулятивное логистическое распределение). Практическое значение логистическое регрессии заключается в том, что она является мощным статистическим методом предсказания событий, который включает в себя одну или несколько независимых переменных. Это востребовано в следующих ситуациях: замеры успешности проводимых рекламных кампаний; прогноз прибыли с определённого товара; оценка вероятности землетрясения в конкретную дату.

5. Метод опорных векторов (SVM) Это целый набор алгоритмов, необходимых для решения задач на классификацию и регрессионный анализ. Исходя из того что объект, находящийся в N-мерном пространстве, относится к одному из двух классов, метод опорных векторов строит гиперплоскость с мерностью (N – 1), чтобы все объекты оказались в одной из двух групп. На бумаге это можно изобразить так: есть точки двух разных видов, и их можно линейно разделить. Кроме сепарации точек, данный метод генерирует гиперплоскость таким образом, чтобы она была максимально удалена от самой близкой точки каждой группы. SVM и его модификации помогают решать такие сложные задачи машинного обучения, как сплайсинг ДНК, определение пола человека по фотографии, вывод рекламных баннеров на сайты.

6. Метод ансамблей Он базируется на алгоритмах машинного обучения, генерирующих множество классификаторов и разделяющих все объекты из вновь поступающих данных на основе их усреднения или итогов голосования. Изначально метод ансамблей был частным случаем байесовского усреднения, но затем усложнился и оброс дополнительными алгоритмами: бустинг (boosting) – преобразует слабые модели в сильные посредством формирования ансамбля классификаторов (с математической точки зрения это является улучшающим пересечением); бэггинг (bagging) – собирает усложнённые классификаторы, при этом параллельно обучая базовые (улучшающее объединение); корректирование ошибок выходного кодирования. Метод ансамблей – более мощный инструмент по сравнению с отдельно стоящими моделями прогнозирования, поскольку: он сводит к минимуму влияние случайностей, усредняя ошибки каждого базового классификатора; уменьшает дисперсию, поскольку несколько разных моделей, исходящих из разных гипотез, имеют больше шансов прийти к правильному результату, чем одна отдельно взятая; исключает выход за рамки множества: если агрегированная гипотеза оказывается вне множества базовых гипотез, то на этапе формирования комбинированной гипотезы оно расширяется при помощи того или иного способа, и гипотеза уже входит в него.

7. Алгоритмы кластеризации Кластеризация заключается в распределении множества объектов по категориям так, чтобы в каждой категории – кластере – оказались наиболее схожие между собой элементы. Кластеризировать объекты можно по разным алгоритмам. Чаще всего используют следующие: на основе центра тяжести треугольника; на базе подключения; сокращения размерности; плотности (основанные на пространственной кластеризации); вероятностные; машинное обучение, в том числе нейронные сети. Алгоритмы кластеризации используются в биологии (исследование взаимодействия генов в геноме, насчитывающем до нескольких тысяч элементов), социологии (обработка результатов социологических исследований методом Уорда, на выходе дающим кластеры с минимальной дисперсией и примерно одинакового размера) и информационных технологиях.

8. Метод главных компонент (PCA) Метод главных компонент, или PCA, представляет собой статистическую операцию по ортогональному преобразованию, которая имеет своей целью перевод наблюдений за переменными, которые могут быть как-то взаимосвязаны между собой, в набор главных компонент – значений, которые линейно не коррелированны. Практические задачи, в которых применяется PCA, – визуализация и большинство процедур сжатия, упрощения, минимизации данных для того, чтобы облегчить процесс обучения. Однако метод главных компонент не годится для ситуаций, когда исходные данные слабо упорядочены (то есть все компоненты метода характеризуются высокой дисперсией). Так что его применимость определяется тем, насколько хорошо изучена и описана предметная область.

9. Сингулярное разложение В линейной алгебре сингулярное разложение, или SVD, определяется как разложение прямоугольной матрицы, состоящей из комплексных или вещественных чисел. Так, матрицу M размерностью [m*n] можно разложить таким образом, что M = UΣV, где U и V будут унитарными матрицами, а Σ – диагональной. Одним из частных случаев сингулярного разложения является метод главных компонент. Самые первые технологии компьютерного зрения разрабатывались на основе SVD и PCA и работали следующим образом: вначале лица (или другие паттерны, которые предстояло найти) представляли в виде суммы базисных компонент, затем уменьшали их размерность, после чего производили их сопоставление с изображениями из выборки. Современные алгоритмы сингулярного разложения в машинном обучении, конечно, значительно сложнее и изощрённее, чем их предшественники, но суть их в целом нем изменилась. 10. Анализ независимых компонент (ICA) Это один из статистических методов, который выявляет скрытые факторы, оказывающие влияние на случайные величины, сигналы и пр. ICA формирует порождающую модель для баз многофакторных данных. Переменные в модели содержат некоторые скрытые переменные, причем нет никакой информации о правилах их смешивания. Эти скрытые переменные являются независимыми компонентами выборки и считаются сигналами. В отличие от анализа главных компонент, который связан с данным методом, анализ независимых компонент более эффективен, особенно в тех случаях, когда классические подходы оказываются бессильны. Он обнаруживает скрытые причины явлений и благодаря этому нашёл широкое применение в самых различных областях – от астрономии и медицины до распознавания речи, автоматического тестирования и анализа динамики финансовых показателей. Исследование возможности построения гибридной схемы шифрования для алгоритмов машинного обучения на основе алгоритмов криптографического преобразования ГОСТ РФ 28147–89 и алгоритмом Фана и Веркаутерена. Ключевые слова: гомоморфное шифрование, ГОСТ 28147–89, машинное обучение Обеспечение конфиденциальности является одной из основных задач информационной безопасности. С развитием современных технологий увеличился объем сбора, хранения и обработки информации, рост объемов требует внедрения новых методов и алгоритмов анализа данных. Для решения этой задачи часто применяется метод машинного обучения — актуальной и интенсивно развивающейся области знаний, направленной на обработку больших объемов информации. Но активное внедрение приложений интеллектуального анализа данных и алгоритмов машинного обучения позволяют злоумышленникам использовать интеллектуальный анализ данных для получения частной информации. Поэтому встает вопрос о противодействии угрозам путем шифрования конфиденциальных данных и создании таких алгоритмов, которые могли бы обнаружить те же сведения из модифицированных данных так же полностью и правильно, как из исходных данных. Общая схема работы алгоритма, обучения по прецедентам над конфиденциальными данными состоит из двух фаз: обучения и применения, на которой алгоритм работает над вектором признаков, не встречающихся в обучающей выборке. При этом оба этапа проходят в режиме секретности и никакие сведения о работе схемы не раскрываются. Исходные данные и результат работы могут быть доступны только клиенту, отправляющему запрос, а модель получения результата — обрабатывающему серверу.

Рис. 1. Общая схема машинного обучения над зашифрованными данными Общая схема машинного обучения над зашифрованными данными представлена на рисунке 1. Пунктирными линиями выделены зоны конфиденциальности и данные которые доступны в этой области одному из участников. Одиночные стрелки указывают входные данные алгоритма, а двойные стрелки указывают результаты. Наиболее перспективным методом шифрования в схемах машинного обучения является гомоморфное шифрование. Схема шифрования называется гомоморфной для некоторых операций ∈ FM (таких как сложение и умножение), действующих в пространстве сообщений, если существуют соответствующие операции ⋄ ∈ FC, действующие в шифрованном текстовом пространстве, удовлетворяющие свойству: 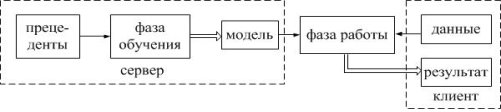$c:\users\шубин\music\44394.001.jpg$

$c:\users\шубин\music\44394.003 (1).png$

Заметим, что это не групповой гомоморфизм в математическом смысле, так как из-за семантической безопасности свойство гомоморфности не коммутируется. То есть, поскольку одно и то же сообщение с высокой вероятностью шифрует различные шифрованные тексты, то:

$c:\users\шубин\music\44394.004.png$

Более того $c:\users\шубин\music\44394.005.png$

Схема гомоморфного шифрования, использующая операции сложения и умножения, получила название полного гомоморфного шифрования, и для нее справедливо следующее условие: 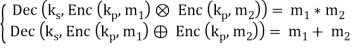$c:\users\шубин\music\44394.006.png$

Но открывшиеся теоретические возможности сдерживаются практическими ограничениями — нельзя говорить о внедрении гомоморфного метода в уже существующие алгоритмы без их существенного изменения: возникают трудности как с логикой построения алгоритма, так и с вычислительными возможностями . Ограничение на работу с целыми числами, количество возможных операций сложения и умножения из-за возрастающего криптографического шума, означает, что на практике гомоморфное шифрование позволяет работать только над зашифрованными данными, представленными в виде полиномов. Но даже в этом случае работа таких алгоритмов будет относительно медленной и ресурсозатратной, а размеры шифротекстов занимают большое пространство в памяти .Так же серьезным ограничением является невозможность использовать какой-либо условный код: операции сравнения, а так же тесты равенства и неравенства, не могут выполняться над зашифрованными данными. Одним из предлагаемых решений проблемы увеличения размера Шифротекста является предварительное шифрование сообщений каким-либо другим стандартом а при обращении к сообщению перекодирование его в гомоморфную схему. Нами была рассмотрена возможность построения гибридной схемы шифрования, основанной на стандарте ГОСТ 28147–89. Идея состоит в упрощении этапа шифрования и отправки Шифротекста клиентом за счет использования более быстродейственного стандарта ГОСТ 28147–89. Полученное сообщение клиент отправляет сервер, где уже вычислительными силами исполнителя производятся вычисления, основанные на методе гомоморфизма. Такое изменение позволит уменьшить объем сообщения, отправляемого клиентом, и вычислительные затраты на криптопреобразование.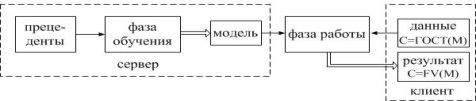

$c:\users\шубин\music\44394.007.jpg$

Рис. 2. Общая схема машинного обучения над зашифрованными данными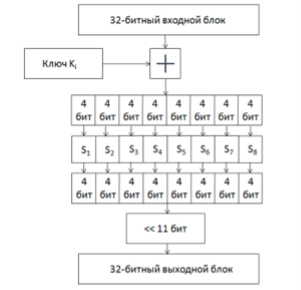

$c:\users\шубин\music\44394.008.png$

Рис. 3. Структура работы ГОСТ 28147–89 Рассмотрим режим простой замены для ГОСТ 28147–89. 64-битный блок открытого текста разбивается на две Части А и В. Для генерации подключей исходный 256-битный ключ разбивается на восемь 32-битных блоков: K1…K8. Ключи K9…K24 являются циклическим повторением ключей K1…K8. Ключи K25…K32 являются ключами K8…K1.

$c:\users\шубин\music\44394.009.png$

$c:\users\шубин\music\44394.011.png$

После выполнения всех 32 раундов алгоритма, блоки A33 и B33 склеиваются. Результат разбивается на восемь 4-битовых последовательностей, каждая из которых поступает на вход своего узла таблицы замен (в порядке возрастания старшинства битов), называемого ниже S-блоком. Общее количество S-блоков стандарта — восемь, то есть столько же, сколько и последовательностей. Каждый S-блок представляет собой перестановку чисел от 0 до 15 (конкретный вид S-блоков в стандарте не определен). В качестве алгоритма, обрабатывающего сообщение на сервере была выбрана схема Fan and Vercauteren. Для обеспечения работы гибридной схемы шифрования необходимо представить схему шифрования ГОСТ 28147–89 как набор операций сложения и умножения, доступных для алгоритма [2]. Так, для выполнения сложения по модулю $c:\users\шубин\music\44394.012.png$ необходимо представить числа в виде суммы а на основе выбранной таблицы замен построить таблицы истинности и вывести СКНФ с избавлением от отрицания для выполнения замен значений без использования операторов сравнения. Теперь подробнее рассмотрим схему [2]. Введем систему обозначений для ее подробного рассмотрения. $c:\users\шубин\music\44394.013.png$

Пусть $c:\users\шубин\music\44394.014.png$ -множество целых чисел, такое, что $c:\users\шубин\music\44394.015.png$ целое число $c:\users\шубин\music\44394.014.png$ равное a mod q и $c:\users\шубин\music\44394.019.png$ -многочлены, коэффициенты которых принадлежат и соответственно. Алгоритм работает с кольцами полиномов $c:\users\шубин\music\44394.021.png$ и $c:\users\шубин\music\44394.022.png$ , где $c:\users\шубин\music\44394.023 (1).png$ , а d-переменная, заданная для конкретного алгоритма. Ограничение $c:\users\шубин\music\44394.025.png$ $c:\users\шубин\music\44394.018.png$

применяется для гарантированного получения случайного полинома необходимой степени.

Полиномы $c:\users\шубин\music\44394.026.png$ , не записаны в функциональной форме $c:\users\шубин\music\44394.027.png$ будут выделены подчеркиванием. Полиномиальное умножение внутри кольца $c:\users\шубин\music\44394.028.png$ так же будет выделено подчеркиванием полиномов, участвующих в операции.

указывает на то, что центрированное сокращение применяется к каждому коэффициенту $c:\users\шубин\music\44394.030.png$ по отдельности, так что $c:\users\шубин\music\44394.031.png$ .Если $c:\users\шубин\music\44394.030.png$ $c:\users\шубин\music\44394.029.png$

получена при помощи равномерного распределения вероятностей на множестве $c:\users\шубин\music\44394.033.png$ это обозначается как $c:\users\шубин\music\44394.034.png$ . Если $c:\users\шубин\music\44394.030.png$ получено при помощи Гауссовского распределения на множестве $c:\users\шубин\music\44394.036.png$ - это обозначает $c:\users\шубин\music\44394.037.png$ .

Пространством сообщений этой схемы является полиномное кольцо $c:\users\шубин\music\44394.038.png$ . Шифрованное текстовое пространство является декартовым произведением двух полиномиальных колец $c:\users\шубин\music\44394.039.png$ , где $c:\users\шубин\music\44394.040.png$ . Прежде чем приступить к шифрованию сообщений, необходимо определить параметры схемы $c:\users\шубин\music\44394.024.png$ определяет степень полиномиальных колец M и C. t и q, определяют множества коэффициентов полиномиальных колец М и С, $c:\users\шубин\music\44394.045 (1).png$

определяет величину случайности, необходимой для обеспечения семантической безопасности.

Генерация ключа. Секретный ключ $c:\users\шубин\music\44394.046.png$ - это переменная, выбранная из $c:\users\шубин\music\44394.047.png$

при помощи равномерного распределения. Открытый ключ, представляет собой вектор , содержащий два многочлена 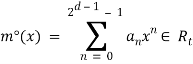: $c:\users\шубин\music\44394.048.png$

$c:\users\шубин\music\44394.049.png$
где $c:\users\шубин\music\44394.034.png$ и $c:\users\шубин\music\44394.050.png$ .

Шифрование $c:\users\шубин\music\44394.051.png$ целочисленное сообщение m представляется как

$c:\users\шубин\music\44394.052.png$ , а заем построить $c:\users\шубин\music\44394.053.png$ , где $c:\users\шубин\music\44394.054.png$ . Шифротекст представляет собой вектор, содержащий два полинома $c:\users\шубин\music\44394.055.png$

где u, $c:\users\шубин\music\44394.057.png$ , $c:\users\шубин\music\44394.058.png$ и $c:\users\шубин\music\44394.059.png$ .
Дешифрование $c:\users\шубин\music\44394.060.png$ : Расшифровка шифрованного текста c производится путем оценки: , $c:\users\шубин\music\44394.062.png$ $c:\users\шубин\music\44394.061.png$
Рассмотрим выполнение операций сложения и умножения над пространством сообщений в алгоритме. Сложение в пространстве шифрованных сообщений выполняется в виде сложения векторов и полиномов с модульной редукцией: $c:\users\шубин\music\44394.063.png$

Умножение в пространстве сообщений приводит к существенному увеличению длины Шифротекст и выполняется по следующей формуле: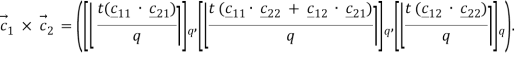

$c:\users\шубин\music\44394.064.png$

При этом можно выполнить дешифрование одного из сообщений, входящих в произведение, изменив функцию дешифрования:

$c:\users\шубин\music\44394.065.png$

Список Литературы

1. S. Laur, H. Lipmaa, T. Mielik¨ainen. Cryptographically private support vector machines // Proceedings of the 12th acm sigkdd international conference on knowledge discovery and data mining ACM, 2006, p. 618–624.

2. T. Graepel, K. Lauter, M. Naehrig. Ml confidential: Machine learning on encrypted data // Information security and cryptology–icisc 2012: Springer, 2013, p. 1–21.

3. R. Bost, R. A. Popa, S. Tu, S. Goldwasser. Machine learning classification over encrypted data, 2014. http://eprint.iacr.org/. ↑19 24 Л. К. Бабенко, Ф. Б. Буртыка, О. Б. Макаревич, А. В. Трепачева

4. J. Wiens, J. Guttag, E. Horvitz. Learning evolving patient risk processes for c. diff colonization // Icml workshop on machine learning from clinical data, 2012.

5. A. Singh, J. V Guttag. A comparison of non-symmetric entropy-based classification trees and support vector machine for cardiovascular risk stratification // Engineering in medicine and biology society, embc, 2011 annual international conference of the ieee IEEE, 2011, p. 79–82.

6. A. Singh, G. Nadkarni, J. Guttag, E. Bottinger. Leveraging hierarchy in medical codes for predictive modeling // Proceedings of the 5th acm conference on bioinformatics, computational biology, and health informatics ACM, 2014, p. 96–103.

7. Yi X., Paulet R., Bertino E. Homomorphic Encryption and Applications. — New York City: Springer International Publishing, 2014. — 136 p. Encrypted statistical machine learning // https://arxiv.org/. URL: https://arxiv.org/pdf/1508.06574v1.pdf

8. Петер Флах. Машинное обучение .Наука и искусство построение алгоритмов Петербург 2016.