Статистика (вопросы для письменного ответа). Вторичной группировкой
 Скачать 56.74 Kb. Скачать 56.74 Kb.
|
|
Перегруппировка уже сгруппированного материала, то есть образование новых групп на основе ранее проведенной группировки, называется вторичной группировкой. К вторичной группировке прибегают: 1) Когда из большого числа первоначально образованных групп надо получать меньшее число более крупных, более характерных групп. Или наоборот, из небольшого числа получить большее число менее крупных групп. 2) Когда в целях сравнения нужно привести в сопоставимый вид по-разному сгруппированный материал. Абсолютные показатели отражают «физические» характеристики исследуемых процессов и явлений (площадь, массу, объем, пространственно-временные параметры). Абсолютные величины в статистике являются исходной базой статистического анализа. Они выражаются в натуральных, условно-натуральных, стоимостных и трудовых единицах. Относительные величины представляют собой результат сравнения (деления) двух показателей. В отличие от абсолютных величин, относительные показатели являются величинами производственными и рассчитываются на основе абсолютных величин. Соотношение между средней арифметической, модой и медианой указывает на характер распределения признака в совокупности, позволяет оценить его ассиметрию. Если Мо<Ме< 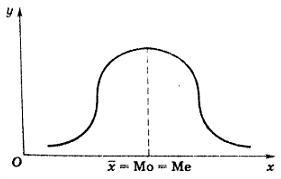 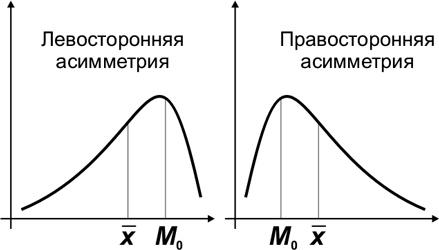 Среднеквадратическое отклонение — наиболее распространённый показатель рассеивания значений случайной величины, относительно её математического ожидания. При ограниченных массивах выборок значений вместо математического ожидания используется среднее арифметическое совокупности выборок. Соотношение среднего квадратического отклонения и среднего линейного отклонения служит индикатором «засоренности» совокупности неоднородными, с основной массой элементов. Чем больше это соотношение, тем больше таких элементов. Среднее линейное отклонение в силу его условности применяется на практике сравнительно редко (в частности, для характеристики выполнения договорных обязательств по равномерности поставки; в анализе качества продукции с учетом технологических особенностей производства). Наиболее совершенной характеристикой вариации является среднее квадратическое отклонение, которое называют стандартом (или стандартным отклонение). По способу построения статистические графики подразделяются на диаграммы, картограммы и картодиаграммы. Диаграмма представляет чертеж, на котором статистическая информация изображается посредством геометрических фигур или символических знаков. Линейные диаграммы широко применяются для характеристики изменений явлений во времени, изучения рядов распределения, выявления связи между явлениями. Для их построения обычно применяется система прямоугольных координат. Геометрическими знаками в линейных диаграммах служат точки, которые последовательно соединяются отрезками прямых линий и складываются в статистическую кривую (ломаную). При построении столбиковых диаграмм также применяется прямоугольная система координат, а статистические данные на них изображаются в виде вертикальных столбиков. Полосовые диаграммы состоят из прямоугольников, расположенных горизонтально (полосами, лентами). В квадратных и круговых диаграммах величина изображаемого явления выражается размером площади. Фигурные диаграммы представляют собой графические изображения в виде рисунков, силуэтов, фигур, соответствующих содержанию статистических данных. Распространенным видом диаграмм являются секторные диаграммы. В них вся величина явления принимается за 100%, а доли отдельных его частей определяются в процентах. Диаграмма, называемая по имени русского ученого В. Е. Варзара: "Знак Варзара", представляет собой прямоугольник, у которого один сомножитель принят за основание, другой за высоту, а вся площадь равна произведению. Картограмма – это схематическая карта, или план местности, на которой отдельные территории в зависимости от величины изображаемого показателя обозначаются с помощью графических символов (точек, расцветок, штриховки). Бывает фоновая и точечная. В фоновых картограммах территории с различной величиной показателя имеют различную штриховку или цвет, например, карта плотности населения на 1 кв. км. по областям страны. В точечных картограммах количество точек одинакового размера (условная единица - величина) на определенной территории характеризует размер изучаемого явления. Они часто применяются для исследования спроса и предложения на товары по регионам. Принцип построения картодиаграммы заключается в том, что на контурной карте составные части диаграммы (столбики, круги) размещаются на площади, отведенной определенной территории. Её преимущество перед диаграммой состоит в том, что она дает представления о величине изучаемого показателя на различных территориях и изображает пространственно размещение изучаемого явления. В зависимости от формы применяемых графических образов статистические графики могут быть точечными, линейными, плоскостными и фигурными. В зависимости от целевого применения статистические графики классифицируются на графики: рядов распределения; структуры статистической совокупности; рядов динамики; показателей связи; показателей выполнения обязательств, договоров и т. д. Статистика — это общетеоретическая наука (комплекс научных дисциплин), которая изучает количественную сторону качественно определенных массовых социально-экономических явлений и процессов, их состав, распределение, размещение в пространстве, движение во времени выявляя действующие взаимозависимости и закономерности в конкретных условиях места и времени. Для анализа рядов распределения чаще всего используют их графическое изображение, которое позволяет судить о форме распределений единиц совокупности по значениям группировочного признака. Дискретный ряд изображается на графике в виде ломаной линии – полигона распределения. 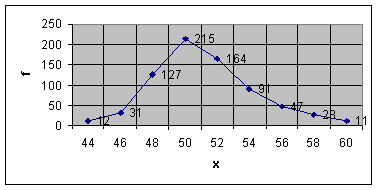 Интервальные ряды изображаются в виде гистограмм распределения (то есть столбиков диаграмм) при этом основанием каждого прямоугольника служит величина соответствующего интервала, а высотой его частотная характеристика. 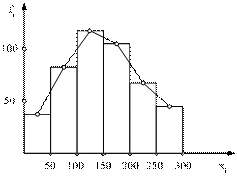 Любая гистограмма может быть преобразована в полигон распределений, для этого необходимо соединить между собой отрезками прямой вершины ее прямоугольников. Стоимостные единицы измерения служат для определения общего размера различных явлений, несопоставимых между собой в натуральных единицах измерения. Они позволяют оценить общие результаты деятельности предприятий, отраслей, регионов, экономики в целом. В условиях рыночной экономики наибольшее значение и применение имеют стоимостные единицы измерения: рубли, доллары, евро, условные денежные единицы и др. Для оценки социально-экономических явлений и процессов используются показатели в текущих или фактически действующих ценах или в сопоставимых ценах. Медианна – это уровень показателя, который делит некоторый набор данных на две равные половины. В статистике абсолютная частота показывает, какое количество раз конкретное значение появляется в наборе данных. В то же время накопительная частота показывает сумму (или нарастающий итог) всех частот, вплоть до текущей точки в наборе данных. Накопительная частота отвечает на вопрос «сколько раз встречается в списке данное значение?» В результате статистического наблюдения исследователь получает сведения о каждой единице анализируемой совокупности. Эти сведения характеризуют ее с различных сторон, поскольку обладают многочисленными признаками и свойствами, изменяющимися во времени и пространстве. Возникает необходимость в систематизации и обобщении результатов статистического наблюдения для получения сводной характеристики всего объекта при помощи обобщающих показателей. Это дает возможность выявить характерные особенности, специфические черты статистической совокупности в целом и отдельных ее составляющих, обнаружить закономерности изучаемых социально-экономических явлений и процессов. Такую систематизацию называют сводкой первичного статистического материала. Данные, получаемые в результате сводки, необходимы для практической и научно-исследовательской работы. Чтобы сделать эти данные доступными для исследования их необходимо изложить в ясной и доходчивой форме. Общепринятой формой изложения цифровых данных является статистическая таблица. Табличная форма позволяет изложить результаты сводки удобно, компактно, наглядно и рационально. В любой статистической таблице имеются ряд горизонтальных строк и вертикальных граф. Простая сводка статистических данных без распределения единиц совокупности на группы по определенным существенным признакам не позволяет получить полную, достоверную характеристику изучаемого объекта. Эго значит, что статистическая группировка является одним из основных этапов проведения статистического исследования. Статистическая группировка - это разделение общей совокупности единиц объекта наблюдения по одному или нескольким существенным признакам на однородные группы, различающиеся между собой в качественном и количественном отношении и позволяющие выделить социально-экономические типы явлений, изучить структуру совокупности или проанализировать взаимосвязи и взаимозависимости между признаками. Группировки являются важнейшим статистическим методом обобщения статистических данных, основой для правильного исчисления статистических показателей. В основе математики лежит число и все действия, происходящие над ним. В статистике же используют группировки, некое обобщение для группы предметов. Математика даёт максимально точный ответ, а статистика заимствуя принципы и методы других дисциплин, может давать разные ответы, в зависимости от интерпретации (выводов) статистических исследований. Построение статистических группировок осуществляется по следующим этапам: Определение числа групп при построении группировки зависит: • от задач статистического исследования; • признака, положенного в основание группировки; • объема изучаемой совокупности; • степени вариации признака. При решении задачи определения чиста групп важно учитывать признак, по которому осуществляется разбиение единиц совокупности на группы, особенно, если в качестве группировочного выступает качественный признак. Так, группировка сотрудников компании по полу может содержать только две группы: "женский" и "мужской", так как признак "пол" по своей сущности имеет только эти две градации. При построении группировки единиц совокупности по количественному признаку особое внимание необходимо обратить на объем изучаемой совокупности и степень вариации признака, положенного в основание группировки. При анализе совокупностей малого объема не следует образовывать большое количество групп, так как группы будут включать в себя недостаточное число единиц совокупности изучаемого объекта. Показатели, рассчитанные для таких групп, не будут представительными и типичными для каждой выделенной группы. Выделение большого числа групп позволит, с одной стороны, точнее воспроизвести характер изучаемого объекта. С другой стороны, слишком большое число групп затрудняет выявление закономерностей при исследовании социально-экономических явлений и процессов. Степень вариации группировочного признака оказывает существенную роль для определения числа групп. В связи с этим при определении числа групп необходимо принять во внимание размах вариации признака. Можно предположить, что чем больше колеблемость, изменяемость значений признака в совокупности, т.е. чем больше размах вариации изучаемого признака, тем большее число групп можно образовать. Однако при этом может возникнуть проблема получения пустых групп, т.е. групп, не содержащих ни одной единицы совокупности. Относительный показатель представляет собой результат деления одного абсолютного показателя на другой и выражает соотношение между количественными характеристиками социально-экономических процессов и явлений. Относительные показатели могут выражаться в коэффициентах, процентах, промилле, продецимилле или быть именованными числами. Если база сравнения принимается за 1, то относительный показатель выражается в коэффициентах, если база принимается за 100, 1000 или 10 000, то относительный показатель соответственно выражается в процентах (%), промилле (%0) и продецимилле (% 00). При изучении социально-экономических явлений и процессов статистика встречается с разнообразной вариацией признаков, характеризующих отдельные единицы совокупности. Величины признаков колеблются, варьируют под действием различных причин и условий, которые в статистике называются факторами. Нередко эти факторы действуют в противоположных направлениях и сами, в свою очередь, варьируют. Среди них есть существенные факторы, определяющие величину вариантов данного признака у всех единиц совокупности. Но есть и несущественные (чисто случайные), которые на одни единицы совокупности могут оказывать влияние, на другие нет. Например, курсы акций, объем спроса и предложения, % ставки в разные периоды. Вариация экзаменационной оценки студентов вызывается такими существенными факторами: - различными способностями студентов - посещаемостью занятий - временем затраченных на подготовку к экзамену - различными социально-бытовыми условиями и т.д. И случайные факторы, которые могут повлиять на оценку: временное недомогание, застряли в лифте, проспали и.д. Результаты сводки и группировки материалов статистического наблюдения, как правило, излагаются в виде статистических таблиц. Однако не всякая таблица является статистической (например, таблица умножения). Статистическую таблицу от других табличных форм отличает следующее: она должна содержать результаты подсчета эмпирических данных; она является итогом сводки первоначальной информации. Статистической называется таблица, которая содержит сводную числовую характеристику изучаемой совокупности по одному или нескольким существенным признакам, взаимосвязанным логикой экономического анализа. Главной задачей статистики является получение и соответствующая обработка статистической информации для принятия решений направленных на достижение желаемого результата в хозяйственной, социально-экономической, научной, культурной и других видах деятельности государства, общественных организаций, экономических структур общества и т.д. и т.п. Основными задачами статистики являются: 1) сбор данных о социально-экономическом положении страны, ее регионов, отраслей экономики, предприятий; 2) разработка и совершенствование научно обоснованной статистической методологии, соответствующей потребностям общества на современном этапе и международным стандартам; 3) разработка и анализ экономико-статистической информации; 4) изучение динамики социально-экономических явлений, прогнозирование и выявление основных тенденций развития; 5) изучение связей между явлениями общественной жизни и степени влияния их друг на друга; 6) научное исследование, обогащение и углубление теоретического познания явлений на основе изучения систем статистических показателей. Система статистических показателей используется при анализе результатов для получения обоснованных выводов о состоянии изучаемого объекта и закономерностях его развития. Для этого применяются обобщающие статистические показатели: абсолютные, относительные и средние величины, вариации и статистические индексы. Выявляются причинно-следственные связи, закономерности, оценивается эффективность и возможности экономических и социальных явлений. Средние величины - это величины, которые позволяют охарактеризовать явление по количественно варьирующему признаку. Простая средняя считается по не сгруппированным данным, взвешенная средняя считается по сгруппированным данным. Средняя арифметическая простая – самый распространенный вид средней. Она равна сумме отдельных значений признака, деленной на общее число этих значений. Средняя арифметическая взвешенная применяется в тех случаях, когда данные представлены в виде рядов распределения или группировок. Она вычисляется как сумма произведений вариантов на соответствующие им частоты, деленная на сумму частот всех вариантов. В ходе анализа средних величин возникает вопрос степени колеблемости, степени вариации, скрывающейся за средней величиной. Для характеристики колеблемости признака в изучаемой совокупности явлений применяются следующие показатели: Размах вариации; Среднее линейное отклонение; Дисперсия; Среднее квадратическое отклонение; Коэффициент. Графики придают статистическим данным предметно-образное выражение, делают их более доступными для восприятия, чем непосредственно числовое (цифровое) выражение этих данных. Они дают более наглядное и доходчивое отображение социально-экономических процессов. В статистических графиках выразительнее сравнительные характеристики, отчетливее видны взаимосвязи, тенденции в развитии явлений. Они облегчают восприятие материала, проведение анализа. Статистические графики отличаются от других графиков тем, что они всегда изображают статистические показатели, дают представление о социально-экономическом явлении или процессе. Статистическим графиком называют чертеж, на котором с помощью условных геометрических образов или знаков описываются в различных разрезах те или иные совокупности. Статистические карты представляют собой вид графических изображений статистических данных на схематичной географической карте, характеризующих уровень или степень распространения того или иного явления на определенной территории. Средствами изображения территориального размещения являются штриховка, фоновая раскраска или геометрические фигуры. Различают картограммы и картодиаграммы. Статистический показатель – это качественно определенная переменная величина, количественно характеризующая объект исследования или его свойства. Качественную определенность обеспечивает набор признаков, содержащихся в его определении. Количественная определенность показателя связана с признаками места и времени. Статистические показатели определяются путем суммирования абсолютных значений признака (численность населения, безработных, трудовых ресурсов), вычисления средних значений признаков (средняя заработная плата, средний доход на душу населения), относительных величин (индекс себестоимости, темпы прироста). В зависимости от охвата единиц изучаемой статистической совокупности показатели подразделяются на индивидуальные и сводные. Индивидуальные показатели характеризуют отдельный объект или отдельную единицу совокупности – предприятие, фирму, банк, домохозяйство и т. п. Примером индивидуальных абсолютных показателей может служить численность промышленно-производственного персонала предприятия, оборот торговой фирмы, совокупный доход домохозяйства. Индивидуальный относительный показатель представляет собой результат соотнесения двух индивидуальных абсолютных показателей, характеризующих один и тот же объект или единицу совокупности. Например, рентабельность продукции отдельного предприятия получают как отношение прибыли от реализации продукции и услуг к затратам на их производство и реализацию. Сводные показатели в отличие от индивидуальных характеризуют группу единиц, представляющую собой часть статистической совокупности или всю совокупность в целом. Эти показатели, в свою очередь, подразделяются на объемные и расчетные. Объемные показатели получают путем сложения значений признака отдельных единиц совокупности. Полученная величина, называемая объемом признака, может выступать в качестве объемного абсолютного показателя (например, стоимость основных фондов всех предприятий отрасли), а может сравниваться с другой объемной абсолютной величиной (например, с численностью промышленно-производственного персонала этих предприятий) или объемом совокупности (в данном примере – с числом предприятии). В последних двух случаях получают объемный относительный и объемный средний показатели (соответственно – фондовооруженность и средняя стоимость основных фондов). Расчетные показатели, вычисляемые по различным формулам, служат для решения отдельных статистических задач анализа – измерения вариации, характеристики структурных сдвигов, оценки взаимосвязи и т. д. Они также делятся на абсолютные, относительные или средние. В эту группу входят индексы, коэффициенты тесноты связи, ошибки выборки и прочие показатели, подробно рассмотренные ниже в соответствующих главах. Статистический показатель дает количественно-качественную оценку свойств изучаемых явлений. Статистический показатель строится как обобщающая характеристика признака, чем отличается от индивидуальных значений (признаков). Например, продолжительность жизни индивидуума представляет собой признак, а средняя продолжительность ожидаемой жизни родившегося поколения — показатель. Он может исчисляться как среднее значение признаков, сумма абсолютных значений признака и вычисление относительных величин. Методика исчисления статистических показателей постоянно совершенствуется: от исчисления некоторых показателей за ненадобностью отказываются, в то же время появляются новые, более точные. Так, в современных условиях особое значение для международных сравнений, диагностики состояния экономики страны имеют макроэкономические показатели (ВНД, ВВП, уровень занятости, индекс инфляции и т.д.). Эти показатели публикуются в специальных статистических сборниках, Средняя величина – это обобщающая характеристика единиц совокупности по какому–либо варьирующему признаку. Величина средней дает обобщающую количественную характеристику всей совокупности и характеризует ее в отношении данного признака. В качестве структурных средних чаще всего используют показатели моды – наиболее часто повторяющегося значения признака – и медианы – величины признака, которая делит упорядоченную последовательность его значений на две равные по численности части. В итоге у одной половины единиц совокупности значение признака не превышает медианного уровня, а у другой – не меньше его. Мода представляет наиболее часто встречающееся или типичное значение. Мода применяется в коммерческой практике для изучения покупательского спроса и регистрации цен. Медиана – это элемент, который больше или равен и одновременно меньше или равен половине остальных элементов ряда распределения. Свойство медианы заключается в том, что сумма абсолютных отклонений значений признака от медианы меньше, чем от любой другой величины. Вариация – колеблемость, многообразие, изменяемость величины признака у отдельных единиц совокупности. Она возникает в результате того, что индивидуальные значения признака складываются под влиянием разнообразных факторов (условий), которые по-разному сочетаются в каждом отдельном случае. К показателям вариации относятся: I группа — абсолютные показатели вариации размах вариации среднее линейное отклонение дисперсия среднее квадратическое отклонение II группа — относительные показатели вариации коэффициент вариации коэффициент осцилляции относительное линейное отклонение Экспликация графика - это пояснение его содержания, включающее в себя заголовок графика, объяснения масштабных шкал, пояснения отдельных элементов графического образа. Заголовок графика в краткой и четкой форме поясняет основное содержание изображаемых данных. Помимо заголовка на графике дается текст, делающий возможным чтение графика. Цифровые обозначения шкалы дополняются указанием единиц измерения. Все буквенные и цифровые значения должны располагаться на графике так, чтобы их легко можно было отсчитывать от начала масштабной шкалы. Ряды цифровых данных, отображающие изменения показателей коммерческой деятельности во времени, размещаются в строгой хронологической последовательности и обязательно по оси абсцисс. Общим требованием графического метода изображения статистических показателей является то, что факторные признаки размещаются на горизонтальной шкале графика и их изменения читаются слева направо, а результативные признаки - по вертикальной шкале и читаются снизу вверх. Это повышает аналитическое значение статистических графиков. При этом важно, чтобы заголовок (титул) графика был бы кратким, но достаточно четко пояснял основное его содержание. |
