Введение 2 Глава Теоретические основы оптимизации инвестиционного портфеля 4
 Скачать 216.51 Kb. Скачать 216.51 Kb.
|
|
ГЛАВА 2. ОПТИМИЗАЦИЯ ИНВЕСТИЦИОННОГО ПОРТФЕЛЯ ПО МЕТОДУ МАРКОВИЦА 2.1 Проблема выбора инвестиционного портфеля В 1952 году Гарри Марковиц опубликовал основополагающую статью, заложившую основу современного подхода теории портфеля к инвестированию. Подход Марковица начинается с предположения, что в настоящее время у инвестора есть определенная сумма для инвестирования. Эти деньги инвестируются в течение периода времени, называемого периодом владения. В конце периода владения инвестор продает ценные бумаги, купленные в начале периода, а затем использует полученную выручку для потребления или реинвестирования в различные ценные бумаги (или и то, и другое). Таким образом, подход Марковица можно рассматривать как дискретный подход, в котором начало периода обозначается как t=0, а конец периода обозначается как t=1. В момент времени t = 0 инвестор решает купить определенную ценную бумагу в портфеле к моменту времени t = 1. Поскольку портфель представляет собой набор различных ценных бумаг, это решение эквивалентно выбору оптимального портфеля из набора возможных портфелей. Поэтому эту проблему часто называют проблемой выбора инвестиционного портфеля. Принимая решение в момент времени t = 0, инвестор должен иметь в виду, что доходность ценной бумаги (и, следовательно, доходность портфеля) в следующем периоде владения неизвестна. Однако инвестор может оценить ожидаемую (или среднюю) доходность различных ценных бумаг на основе некоторых предположений и инвестировать в ценную бумагу с наивысшей ожидаемой доходностью. Марковиц говорит, что в целом это неразумно, потому что типичный инвестор хочет «высокой прибыли», но при этом ищет «наиболее надежную возможную прибыль». Это означает, что инвестор, стремящийся максимизировать ожидаемую прибыль и минимизировать неопределенность (т. е. риск), имеет две конкурирующие цели, которые должны быть сбалансированы при принятии решения о покупке в момент времени t = 0. Это означает, что Подход Марковица к принятию решений позволяет адекватно решать обе эти задачи. В результате наличия двух противоречивых целей вам следует диверсифицироваться, покупая несколько ценных бумаг вместо одной. Последующее обсуждение подхода Марковица к инвестированию начинается с более конкретного определения понятий начального и конечного богатства. Согласно уравнению доходность ценной бумаги за один период можно рассчитать следующим образом: 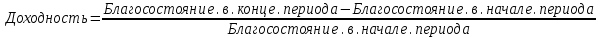 где «начальный актив» — цена покупки одной ценной бумаги данного типа (например, 1 обыкновенной акции компании) в момент времени t = 0, а «конечный актив» — рынок. Стоимость этой ценной бумаги в момент времени t = 1 равна сумме всех выплат наличными (или наличными) держателям этой ценной бумаги в период с момента времени t = 0 до момента времени t = 1. Аналогичным образом можно рассчитать доходность ценных бумаг. 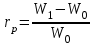 Здесь W0 обозначает совокупную цену покупки всех ценных бумаг, входящих в портфель в момент t = 0; W1 - совокупную рыночную стоимость этих ценных бумаг в момент t = 1 и, кроме того, совокупный денежный доход от обладания данными ценными бумагами с момента t = 0 до момента t = 1. Уравнение с помощью алгебраических преобразований может быть приведено к виду: 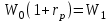 Уравнение говорит нам, что начальное богатство или богатство в начале периода (W0), умноженное на 1, и сумма доходности портфеля равняется богатству в конце периода (W1). ), или конечное богатство. Ранее мы упоминали, что инвестор должен решить, какой портфель покупать в момент времени t = 0. Делая это, инвестор понятия не имеет, какова будет ожидаемая стоимость большинства различных альтернативных портфелей. Он не знает, какова будет доходность большинства этих портфелей. Следовательно, согласно Марковицу, инвесторы должны относиться к норме доходности, связанной с любым из этих портфелей, как к случайной величине. Следовательно, переменные имеют свои собственные свойства, одно из которых — ожидаемое (или среднее) значение, а другое — стандартное отклонение. Марковиц утверждает, что инвесторы должны выбирать портфели исключительно на основе ожидаемой доходности и стандартных отклонений. Это означает, что инвестор должен оценить ожидаемую доходность и стандартное отклонение каждого портфеля и выбрать «лучший» на основе их соотношения. Интуиция играет в этом решающую роль. Ожидаемый доход может быть выражен как мера потенциального вознаграждения, связанного с конкретным портфелем, а стандартное отклонение может быть выражено как мера риска, связанного с этим портфелем. Поэтому, рассмотрев каждый портфель с точки зрения потенциальных выгод и рисков, инвесторы должны выбрать тот портфель, который им больше всего подходит. Предположим, что два альтернативных портфеля обозначены буквами А и В. Эти портфели показаны в таблице 1. Портфель A имеет ожидаемую годовую доходность 8%, а портфель B имеет ожидаемую годовую доходность 12%. Предположим, у инвестора есть первоначальный капитал в размере 100 000 и период владения 1 год. Это означает, что ожидаемый окончательный уровень благосостояния, связанный с портфелями A и B, составляет 108 000 и 112 000 соответственно. Исходя из этого, можно сделать вывод, что портфель Б более уместен. Однако годовые стандартные отклонения для портфелей A и B составляют 10% и 20% соответственно. Таблица 2.1 - Сравнение уровней конечного благосостояния двух гипотетических портфелей
Как показано в Таблице 2.1, это означает, что при наличии портфеля B существует 2%-ная вероятность того, что конечное богатство инвестора составит 70 000 или меньше, но в действительности, когда портфель A куплен, это означает, что вероятность того, что конечное богатство инвестора быть меньше 70 000 равно нулю. Точно так же у портфеля B есть 5%-ная вероятность того, что у него останется менее 80 000, а у портфеля A — нулевая вероятность. Более пристальный взгляд показывает, что у портфеля B есть 14 % шансов упасть ниже 90 000, а у портфеля A — 4 %. Более того, существует 27%-ная вероятность того, что в портфеле B окажется меньше 100 000, тогда как для портфеля A такая вероятность составляет всего 21%. Поскольку инвестор имеет первоначальный капитал в размере 100 000, это означает, что он с большей вероятностью получит отрицательный доход (27%) от покупки портфеля B, чем от покупки портфеля A (21%). Наконец, из таблицы 1 видно, что портфель А является менее рискованным портфелем, чем портфель Б. Так что лучше в этом смысле. Окончательное решение о покупке портфеля A или B зависит от отношения конкретного инвестора к риску и доходности. Метод, применяемый для выбора наиболее желательного портфеля, использует так называемую кривую безразличия. Эти кривые отражают отношение инвесторов к риску и доходности и могут быть представлены в виде двумерных графиков. где горизонтальная ось — это риск, измеряемый стандартным отклонением (обозначается ), а вертикальная ось — измеренное вознаграждение. По ожидаемой доходности (уточненной). На гипотетическом графике кривой безразличия инвесторов каждая кривая представляет собой одну кривую безразличия инвесторов, представляющую собой комбинацию всех портфелей, обеспечивающих определенный уровень аппетита инвесторов. Отсюда вытекает первое важное свойство кривой безразличия. Другими словами, все портфели, лежащие на определенной кривой безразличия, эквивалентны инвестору. Следствием этого свойства является невозможность пересечения кривых безразличия. Это приводит ко второму важному свойству кривой безразличия. Инвесторы обнаружат, что портфели с кривой безразличия вверху слева более привлекательны, чем портфели с кривой безразличия внизу справа. В заключение, инвесторы должны знать, что существует бесконечное количество кривых безразличия. Это просто означает, что независимо от того, как вы расположите две кривые безразличия на графике, всегда есть возможность создать между ними третью кривую. Тут уместно спросить. Как инвестор может определить форму своей кривой безразличия В конечном итоге каждый инвестор будет иметь график кривой безразличия. Он обладает всеми вышеперечисленными характеристиками и в то же время является сугубо индивидуальным для каждого инвестора. Один метод требует, чтобы инвестор ознакомился с набором гипотетических портфелей и их ожидаемой доходностью и стандартными отклонениями. Из них он должен выбрать наиболее привлекательную. На основе сделанного выбора можно оценить форму и положение кривой безразличия инвестора. Предполагается, что каждый инвестор действует так, как если бы он основывал свой выбор на кривой безразличия, даже если он сознательно не использует эту кривую. В заключение, у каждого инвестора есть график кривой безразличия, представляющий их выбор ожидаемой доходности и стандартного отклонения. Для этого инвестор определяет ожидаемую доходность и стандартное отклонение для каждого потенциального портфеля, наносит их на график, а затем выбирает один портфель на кривой безразличия выше и левее другой кривой. При обсуждении кривых безразличия мы сделали два неявных предположения. Во-первых, ожидается, что инвестор будет выбирать между двумя портфелями, которые в остальном идентичны по ожидаемой доходности, и выбирать портфель с более высокой ожидаемой доходностью. При использовании подхода Марковица делается предположение о десатурации. То есть предполагается, что инвесторы предпочитают более высокий уровень конечного благосостояния более низкому. Это связано с тем, что чем выше ваш предельный уровень благосостояния, тем больше вы можете потратить на потребление в момент времени t = 1 (или дальше в будущем). Следовательно, имея два портфеля с одинаковым стандартным отклонением, инвестор выберет портфель с более высокой ожидаемой доходностью. Однако все не так просто, когда инвестору необходимо выбирать из портфелей с одинаковым уровнем ожидаемой доходности, но разными уровнями стандартного отклонения. Здесь стоит рассмотреть второе предположение о том, что инвесторы не склонны к риску. В общем случае предполагается, что инвесторы не склонны к риску. Он выбирает портфель с меньшим стандартным отклонением. Что значит быть не склонным к риску Это означает, что инвестор, у которого есть выбор, не хочет выбирать «честную игру», где ожидаемое вознаграждение по определению равно нулю. Например, предположим, что вы подбрасываете монету и платите 5 долларов за выпадение орла и 5 долларов за решку. Вероятность выпадения орла (или решки) составляет 50%, поэтому ожидаемое вознаграждение равно 0 долларов США [(0,5 x 5 долларов США) + (0,5 x (-5 долларов США)]. Поэтому не склонные к риску инвесторы инстинктивно избегают этой игры. Это связано с тем, что «количество разочарования» потенциальных потерь выше, чем «количество удовольствия» потенциальных выигрышей. Эти два предположения о снижении насыщения и неприятии риска объясняют выпуклость и положительный наклон кривой безразличия. Несмотря на предположение, что все инвесторы не склонны к риску, мы не можем предположить, что все инвесторы имеют одинаковую степень неприятия риска. Некоторые инвесторы очень не склонны к риску, в то время как другие несколько не склонны к риску. Это означает, что разные инвесторы имеют разные кривые безразличия. 2.2 Вычисление ожидаемой доходности и стандартных отклонений портфелей В предыдущем разделе мы обсудили вопросы выбора портфеля, с которыми сталкиваются все инвесторы. Он также рассказал об инвестиционном подходе Гарри Марковица как способе решения этой проблемы. Этот подход требует от инвесторов оценки всех альтернативных портфелей с точки зрения ожидаемой доходности и стандартных отклонений с использованием кривых безразличия. Если инвестор не склонен к риску, то для инвестиций выбирается портфель, лежащий на кривой безразличия и «выше и левее» всех остальных. Однако некоторые вопросы остаются без ответа. Например, как инвестор рассчитывает ожидаемую доходность и стандартное отклонение портфеля. а) Не склонные к риску инвесторы б) Инвесторы со средним неприятием риска в) Инвесторы с низким уровнем неприятия риска 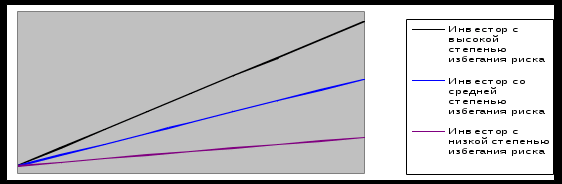 Рисунок 2.1 - Кривые безразличия инвесторов с различной степенью избегания риска Исходя из подхода Марковица к инвестированию, особое внимание инвесторам следует уделять конечному (на конец периода) благосостоянию W1. Это означает, что при принятии решения о том, какой портфель купить и использовать первый (на начало периода) актив W0, инвестор должен обратить особое внимание на влияние различных портфелей на W1. Этот эффект может быть представлен ожидаемой доходностью и стандартным отклонением для каждого портфеля. Как упоминалось ранее, портфель представляет собой набор различных ценных бумаг. Поэтому кажется логичным, что ожидаемая доходность и стандартное отклонение портфеля зависят от ожидаемой доходности и стандартного отклонения каждой ценной бумаги в портфеле. Также ясно, что большое влияние оказывает то, какая часть начального капитала вложена в ту или иную ценную бумагу. Ожидаемая доходность портфеля может быть рассчитана несколькими способами, каждый из которых дает одинаковые результаты. Первый метод рассчитывает ожидаемую цену портфеля в конце периода и использует формулу для расчета нормы прибыли. Следовательно, начальная стоимость портфеля (W0) вычитается из ожидаемой стоимости портфеля в конце периода (W1) и эта разница делится на начальную стоимость портфеля (W0) для получения этих результатов. Операция – это ожидаемая доходность портфеля. Эта процедура может быть применена к любому количеству ценных бумаг в вашем портфеле. Другой способ расчета ожидаемой доходности портфеля. Эта процедура рассчитывает ожидаемую доходность портфеля как средневзвешенную ожидаемую доходность ценных бумаг, составляющих портфель. В качестве весов используются относительные рыночные цены ценных бумаг в портфеле. Общее правило расчета ожидаемой доходности портфеля из N ценных бумаг имеет символическую форму: 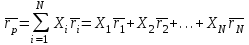 где rp - ожидаемая доходность портфеля; Хi - доля начальной стоимости портфеля, инвестированная в ценную бумагу; ri - ожидаемая доходность ценной бумаги I; N - количество ценных бумаг в портфеле. Следовательно, вектор ожидаемой доходности можно использовать для вычисления ожидаемой доходности любого портфеля из N ценных бумаг. Вектор состоит из одного столбца чисел, где i-я строка содержит ожидаемую доходность i-й ценной бумаги. Поскольку ожидаемая доходность портфеля представляет собой средневзвешенную ожидаемую доходность ценных бумаг, вклад каждой ценной бумаги в ожидаемую доходность портфеля зависит не только от ее доли в начальной рыночной стоимости портфеля, но и от ее ожидаемой доходности. Вложился в эту безопасность. Остальные факторы значения не имеют. Уравнение (4) просто означает, что инвестор, желающий получить максимально возможную ожидаемую доходность, должен иметь портфель из одной ценной бумаги с максимально возможной ожидаемой доходностью. Немногие инвесторы делают это, и лишь немногие инвестиционные консультанты советуют такую экстремальную политику. Вместо этого инвесторы должны диверсифицировать свои портфели. Портфель должен содержать несколько ценных бумаг. Это имеет смысл, потому что диверсификация может снизить риск, измеряемый стандартным отклонением. Любая полезная мера риска должна каким-то образом учитывать вероятность и величину возможных «плохих» результатов. Вместо измерения вероятностей различных результатов измерение риска требует некоторого способа оценки того, насколько вероятно, что фактический результат будет отличаться от ожидаемого результата. Стандартное отклонение — это мера, которая позволяет это сделать, поскольку это расчетное отклонение фактической доходности от ожидаемого значения. Простая мера риска может показаться в лучшем случае очень грубой суммой «плохих» возможностей. Однако в наиболее типичных обстоятельствах стандартное отклонение на самом деле является очень хорошей мерой степени неопределенности в оценке перспектив портфеля. Лучший пример — это когда распределение вероятностей доходности портфеля может быть аппроксимировано знакомой колоколообразной кривой, называемой нормальным распределением. Это часто рассматривается как правдоподобное предположение при анализе эффективности диверсифицированных портфелей, когда исследуемый период владения относительно невелик (до 1/4). Это поднимает вопрос о стандартном отклонении как мере риска. Почему мы должны учитывать «сюрпризы» (т. е. случаи, когда доходность выше ожидаемой) при измерении риска? Почему не учитывать отклонения ниже ожидаемой доходности? Однако, если распределение вероятностей симметрично, как и нормальное распределение, результат будет таким же. Почему? Потому что левая часть симметричного распределения является зеркальным отражением правой части. Таким образом, список портфелей, упорядоченный по «риску снижения», не будет отличаться от списка, упорядоченного по стандартному отклонению, если бы доходность распределялась нормально. Например, Гарри Марковиц изначально (в своей оригинальной работе об эффективных множествах) предполагал, что меры риска включают только отрицательные результаты. Позже он отказался от этого подхода в пользу стандартного отклонения, чтобы упростить расчеты. Неважно, что расчет включает в себя результаты, которые превышают и те, которые не превышают. Стандартное отклонение суммирует «плохую» часть распределения дохода от инвестиций. Но что, если доход от инвестиций не распределяется нормально? Мы можем представить ситуации, в которых доходность обыкновенных акций не соответствует этому предположению. Предположим, инвестор на рынке обычных акций сталкивается с ограниченной ответственностью. В этом случае самое большое, что он может потерять, — это первоначальные вложения. При этом потенциальные выгоды от повышения не ограничены. Наконец, мы ожидаем, что доходность большинства обыкновенных акций упадет до среднего уровня по рынку. То, что вы только что описали, называется распределением со сдвигом вправо по отношению к нормальному распределению. Стандартное отклонение неадекватно характеризует риск «правого сдвига» ценных бумаг. При этом игнорируется тот факт, что большая часть волатильности ценной бумаги находится на «хорошей» стороне ожидаемой доходности ценной бумаги. Интересно, что распределения со сдвигом вправо можно свести к нормальным распределениям с помощью простых математических манипуляций. Если вы добавите 1 к доходности ценной бумаги, а затем рассчитаете натуральный логарифм этого значения, результирующее распределение преобразованных доходностей может быть нормальным. Поэтому исследователей часто интересует, удовлетворяет ли доходность ценной бумаги «логарифмически нормальному» распределению, а не нормальному. Хотя эмпирические данные могут быть противоречивыми, большинство экспертов считают, что «логарифмическая нормальность» является хорошей мерой доходности обыкновенных акций. Однако доходность некоторых ценных бумаг не является нормально распределенной или «логарифмически нормально распределенной». Самый простой пример — опцион. Например, колл-опцион позволяет его владельцу получить прибыль в случае положительной доходности связанной акции, но в то же время избежать убытков в случае отрицательной доходности связанной акции. . По сути, колл-опцион обрывает распределение доходности акций в точке, где начинается убыток. Следовательно, инвестору принадлежит только «хорошая» или правильная сторона распределения прибыли. Таким образом, доходность колл-опционов по определению не распределяется нормально. Кроме того, некоторые ценные бумаги содержат опционы. Например, облигация с регрессом может быть погашена по усмотрению эмитента. Они делают это только в том случае, если процентные ставки меняются в их пользу. Более сложная мера риска доходности ниже ожидаемой осуществляется с использованием набора статистических данных, известных как парциальные моменты более низкого порядка. Полудисперсия аналогична дисперсии, но в расчетах используются только доходы, которые, вероятно, упадут ниже ожидаемого дохода. Полудисперсия — это меньшее стандартное отклонение ожидаемой доходности, что делает ценные бумаги с относительно большим потенциальным дефицитом менее привлекательными. Для ценных бумаг с ненормальной и «логарифмически нормальной» доходностью эти меры риска являются более интуитивными и гибкими, чем традиционные меры риска. Стандартное отклонение измеряется на основе среднего значения распределения доходов. Однако инвестор может захотеть оценить инвестиции, используя какое-либо значение в качестве цели, например, норму доходности рыночного индекса или простое число, такое как 0%. Измеритель риска потерь может учитывать все эти предпочтения. Однако есть некоторые проблемы с использованием измерителя риска потерь. В частности, игнорируется возможность превышения целевого дохода. Вместо использования этих индикаторов риска можно напрямую учитывать предвзятость в ценообразовании инвестиций. В качестве альтернативы мы можем предположить, что инвесторы анализируют потенциальные инвестиции с точки зрения величины сдвига вправо, а также ожидаемой доходности и стандартного отклонения. По сути, риск является многомерным, поскольку включает в себя как стандартное отклонение, так и погрешность. Если две инвестиции имеют одинаковую ожидаемую доходность и стандартное отклонение, предпочтение отдается той инвестиции, которая больше всего смещена вправо. Нельзя ожидать, что мера риска даст точные результаты во всех ситуациях. Стандартное отклонение доказало свою эффективность в большинстве ситуаций, с которыми сталкиваются практики. Если это не подходящая мера, альтернативы следует рассматривать не только с точки зрения того, насколько хорошо они описывают распределение доходности, но и сложности, которые они вносят в анализ. Давайте посмотрим, как рассчитывается стандартное отклонение портфеля. Для портфеля, состоящего из трех ценных бумаг, формула выглядит следующим образом: | ||||||||||||||||||||||||||
