Введение 8 Этапы создания Windowsприложения 8
 Скачать 6.98 Mb. Скачать 6.98 Mb.
|
8.6. Обработка квадратных матрицКвадратной называют матрицу, у которой число строк равно числу столбцов. В общем случае обработка квадратных матриц принципиально не отличается от обработки прямоугольной матрицы. Для нее также используют вложенные циклы, с той лишь разницей, что диапазоны значений для внешнего и внутреннего счетчиков будут одинаковыми. Посмотрим, как изменяется текст программы ввода матрицы и вывода ее в окно списка при переходе от прямоугольной матрицы к квадратной. Так как размеры у квадратной матрицы совпадают, то для их хранения достаточно одной переменной. В квадратной матрице n строк и n столбцов. Следовательно, вместо двух блоков ввода (ввод числа строк и ввод числа столбцов) будет один – ввод размера матрицы. Do n = Val(InputBox("Введите размер матрицы")) Loop Until n > 0 Нумерация элементов в квадратной матрице идет также как и в прямоугольной – с нуля. Поэтому номера последней строки и столбца будут на единицу меньше соответствующего размера. n -= 1 Выделяем память для хранения квадратной матрицы. ReDim a(n, n) Организуем вложенные циклы для ввода элементов матрицы. Диапазоны значений счетчиков у этих циклов совпадают, так как совпадают размеры матрицы. For i = 0 To n For j = 0 To n Вводим очередной элемент матрицы. a(i, j) = Val(InputBox("Введите элемент (" + _ Str(i) + "," + Str(j) + ")")) Next Next С завершением вложенных циклов завершается и процесс ввода значений элементов квадратной матрицы. Начинаем процесс вывода матрицы в окно списка. Сначала это окно необходимо очистить от предыдущих результатов работы программы. lstMatrix.Items.Clear() Затем мы выводим поясняющий заголовок. lstMatrix.Items.Add("Матрица") Организуем вложенные циклы для вывода матрицы. Диапазоны значений счетчиков у этих циклов совпадают, так как совпадают размеры матрицы. В остальном процесс вывода квадратной матрицы ничем не отличается от вывода прямоугольной матрицы. For i = 0 To n s = "" For j = 0 To n s += Str(a(i, j)) + vbTab Next lstMatrix.Items.Add(s) Next Полный текст программы обработки квадратной матрицы приведен в приложениях 41 и 42. При обработке квадратных матриц можно использовать все алгоритмы, разработанные для прямоугольных матриц. Но существует ряд задач, характерных именно для квадратных матриц. Это задачи обработки элементов, находящихся на диагоналях матрицы или в одном из ее треугольников. В квадратной матрице выделяют главную и побочную диагонали. Главная диагональ (см. рис. 56) идет из верхнего левого угла матрицы в правый нижний угол, то есть от элемента с индексами (0, 0) до элемента с индексами (n, n), где n – номер последнего столбца и строки матрицы. На каждой строке матрицы находится ровно один элемент, стоящий на главной диагонали. Для этого элемента всегда будет выполняться условие i = j, где i – номер строки, а j – номер столбца. 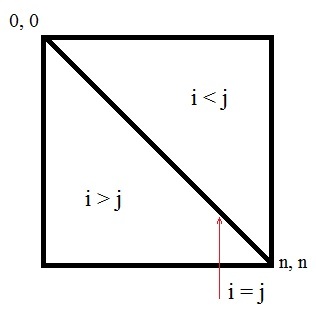 Рис. 56. Главная диагональ квадратной матрицы Главная диагональ разбивает матрицу на два треугольника. Все элементы верхнего треугольника расположены над главной диагональю. Для них выполняется условие i < j, где i – номер строки, а j – номер столбца. Все элементы нижнего треугольника расположены под главной диагональю. Для них выполняется условие i > j, где i – номер строки, а j – номер столбца. Как правило, элементы, стоящие на диагонали, не включаются ни в один треугольник. Если же по условию задачи требуется включить диагональные элементы в один из треугольников, то в соответствующем условии строгое неравенство заменяется на нестрогое. Условия главной диагонали и соответствующих треугольников проиллюстрированы на рис. 56. Побочная диагональ (см. рис. 57) идет из верхнего правого угла матрицы в левый нижний угол, то есть от элемента с индексами (0, n) до элемента с индексами (n, 0), где n – номер последнего столбца и строки матрицы. На каждой строке матрицы находится ровно один элемент, стоящий на побочной диагонали. Для этого элемента всегда будет выполняться условие i + j = n, где i – номер строки, j – номер столбца, n – номер последней строки и последнего столбца матрицы. 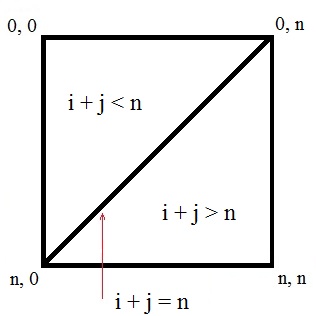 Рис. 57. Побочная диагональ квадратной матрицы Побочная диагональ разбивает матрицу на два треугольника. Все элементы верхнего треугольника расположены над побочной диагональю. Для них выполняется условие i + j < n, где i – номер строки, j – номер столбца, n – номер последней строки и последнего столбца матрицы. Все элементы нижнего треугольника расположены под побочной диагональю. Для них выполняется условие i + j > n, где i – номер строки, j – номер столбца, n – номер последней строки и последнего столбца матрицы. Как правило, элементы, стоящие на диагонали, не включаются ни в один треугольник. Если же по условию задачи требуется включить диагональные элементы в один из треугольников, то в соответствующем условии строгое неравенство заменяется на нестрогое. Условия побочной диагонали и соответствующих треугольников проиллюстрированы на рис. 56. Рассмотрим особенности алгоритма обработки диагональных элементов на примере решения задачи определения суммы элементов, стоящих на главной диагонали, и произведения элементов, стоящих на побочной диагонали. Полученные результаты будем выводить в окно списка. Объявляем переменные для хранения суммы и произведения. Dim sum, proiz As Integer И задаем им начальные значения. sum = 0 proiz = 1 Так как в каждой строке находится ровно один элемент с каждой диагонали, то для их обработки нам достаточно одного цикла, поскольку, зная номер строки, номер столбца можно вычислить, пользуясь условием соответствующей диагонали. Организуем цикл по всем строкам матрицы. For i = 0 To n Для элементов главной диагонали выполняется условие i = j, то есть номер строки совпадает с номером столбца. Следовательно, если элемент стоит на главной диагонали и находится в строке с номером i, то он будет стоять в столбце с номером i. Таким образом, любой элемент с главной диагонали матрицы a(,) можно обозначить a(i, i). Добавляем этот элемент к итоговой сумме. sum += a(i, i) Для элементов побочной диагонали выполняется условие i + j = n. Номер строки i нам известен, равно как и значение переменной n. Следовательно, мы можем из этого условия выразить значение переменной j. j = n - i Тогда, если элемент стоит на побочной диагонали и находится в строке с номером i, то он будет стоять в столбце с номером n - i. Таким образом, любой элемент с побочной диагонали матрицы a(,) можно обозначить a(i, n - i). Включаем этот элемент в искомое произведение. proiz *= a(i, n - i) Next После завершения цикла печатаем полученные результаты. Сначала выводим горизонтальную черту, чтобы зрительно отделить исходные данные от результатов. lstMatrix.Items.Add("------------------------------") Затем печатаем значения суммы и произведения с поясняющим текстом. lstMatrix.Items.Add("Сумма = " + Str(sum)) lstMatrix.Items.Add("Произведение = " + Str(proiz)) Полный текст программы представлен в приложении 41. Пример работы программы приведен на рис. 58. 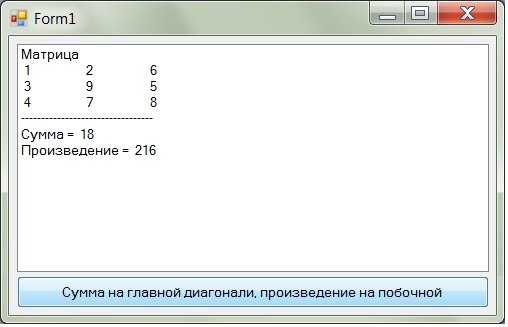 Рис. 58. Пример работы программы вычисления суммы элементов, стоящих на главной диагонали квадратной матрицы, и произведения элементов, стоящих на побочной диагонали квадратной матрицы Теперь рассмотрим особенности алгоритма обработки элементов, принадлежащих к какому-нибудь треугольнику. В качестве примера возьмем задачу поиска минимального из элементов, стоящих выше главной диагонали, и максимального из элементов, стоящих ниже побочной диагонали. Помимо самих значений определим еще индексы искомых элементов. Полученные результаты будем выводить в окно списка. Описываем переменные для хранения минимального и максимального значений, а также их индексов. Dim min, imin, jmin As Integer Dim max, imax, jmax As Integer Зададим начальное значение для минимума. Им может быть любой элемент, который всегда будет принадлежать к нужному треугольнику. Удобнее всего брать элемент, который расположен в вершине прямого угла (см. рис. 56 и рис. 57). Для треугольника, расположенного выше главной диагонали, это будет элемент, находящийся в правом верхнем углу – a(0, n). min = a(0, n) Задаем соответствующие начальные значения индексов. imin = 0 jmin = n Рассуждая аналогичным образом, зададим начальное значение для максимума. Так как нужный треугольник расположен ниже побочной диагонали, то это будет элемент, находящийся в правом нижнем углу – a(n, n). max = a(n, n) Задаем соответствующие начальные значения индексов. imax = n jmax = n Организуем вложенные циклы для обработки всех элементов матрицы. Внешний цикл будет идти по строкам, а внутренний – по столбцам. For i = 0 To n For j = 0 To n На каждом шаге цикла проверяем, принадлежит ли очередной элемент матрицы к треугольнику, расположенному выше главной диагонали, и меньше ли значение этого элемента, чем ранее найденный минимум. If i < j And a(i, j) < min Then Если на оба вопроса дан положительный ответ, значит надо обновить значение минимума, записав в соответствующую переменную значение анализируемого элемента матрицы. min = a(i, j) При этом необходимо еще запомнить индексы текущего элемента. imin = i jmin = j End If Теперь проверяем, принадлежит ли очередной элемент матрицы к треугольнику, расположенному ниже побочной диагонали, и больше ли значение этого элемента, чем ранее найденный максимум. If i + j > n And a(i, j) > max Then Если на оба вопроса дан положительный ответ, значит надо обновить значение максимума, записав в соответствующую переменную значение анализируемого элемента матрицы. max = a(i, j) При этом необходимо еще запомнить индексы текущего элемента. imax = i jmax = j End If Next Next После завершения вложенных циклов в соответствующих переменных хранится искомая информация. Нам остается только вывести ее в окно списка. Сначала выводим горизонтальную строку, чтобы зрительно отделить исходные данные от полученных результатов. lstMatrix.Items.Add("------------------------------") Затем печатаем поясняющий текст и значения необходимых переменных. lstMatrix.Items.Add("Минимум над глав. диагональю") lstMatrix.Items.Add("Значение:" + Str(min)) lstMatrix.Items.Add("Строка:" + Str(imin)) lstMatrix.Items.Add("Столбец:" + Str(jmin)) lstMatrix.Items.Add("Максимум под побоч. диагональю") lstMatrix.Items.Add("Значение:" + Str(max)) lstMatrix.Items.Add("Строка:" + Str(imax)) lstMatrix.Items.Add("Столбец:" + Str(jmax)) Полный текст программы представлен в приложении 42. Пример работы программы приведен на рис. 59. 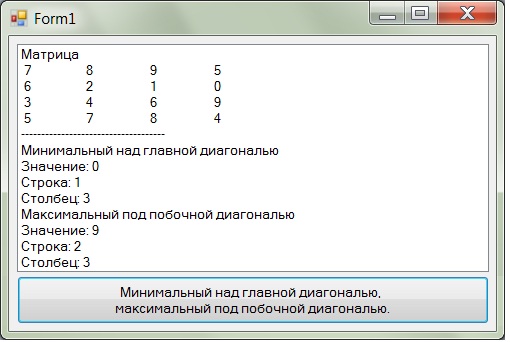 Рис. 59. Пример работы программы поиска минимального из элементов, стоящих выше главной диагонали квадратной матрицы, и максимального из элементов, стоящих ниже побочной диагонали квадратной матрицы Сформулируем основные правила обработки элементов матрицы, стоящих на любой диагонали или принадлежащих к одному из треугольников. Для обработки элементов, стоящих на любой диагонали, достаточно одного цикла. Для обработки элементов, принадлежащих к одному из треугольников, необходимо использовать вложенные циклы. |
