Моделирование система Лабораторная №1. Моделирование систем Лабораторная работа №1. Введение Цель работы

• Название: Введение Цель работы
• Анкор: Моделирование система Лабораторная №1
• Дата: 22.05.2023
• Размер: 1.19 Mb.
• Имя файла: Моделирование систем Лабораторная работа №1 .docx
• Тип: Реферат; #1151625

Введение

Цель работы: Разработка и тестирование конгруэнтного мультипликативного датчика базовой случайной величины (БСВ).

Содержание работы:

1. 
   Выбор параметров датчика БСВ (модуля, множителя и начального значения);
   
2. 
   Реализация датчика БСВ на компьютере;
   
3. 
   Тестирование длины периода датчика БСВ. Длина периода Т должна отвечать требованию Т>10000;
   
4. 
   Тестирование датчика на равномерное распределение;
   
5. 
   Тестирование датчика на независимость БСВ.
   

Результат выполнения лабораторной работы

1. 
   Выбор параметров датчика БСВ
   

В качестве параметров датчика БСВ были взяты следующие значения представленные в таблицы Таблица 1.

Таблица 1. Параметры датчика БСВ

Модуль m	Множитель k
4294965889	371596

В качестве начального значения А₀ = 2.

2. 
   Тестирование длины периода датчика БСВ
   

Оценку длины периода осуществляем путем сравнения начального значения А₀ со всеми последующими числами A_i (i=1…10000). Для этого используем функцию СЧЁТЕСЛИ.

3. 
   Тестирование датчика на равномерное распределение
   

1. 
   Метод моментов.
   

Данный метод заключается в вычислении эмпирических моментов распределения случайной величины (с.в.) по ее выборке и их сравнение с теоретическими моментами. При достаточно большой длине выборки эмпирические моменты с.в., которые являются приближенными оценками моментов, приближаются к точным значениям моментов распределения.

Результат расчета эмпирических и теоретических значений представлен на рисунке 1 и 2.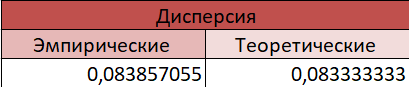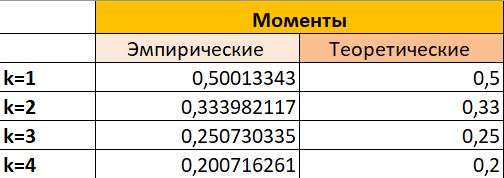




Рисунок 1. Результат расчета эмпирических и теоретических значений

Из рисунка 1 мы видим, что эмпирические значения очень близки к теоретическим.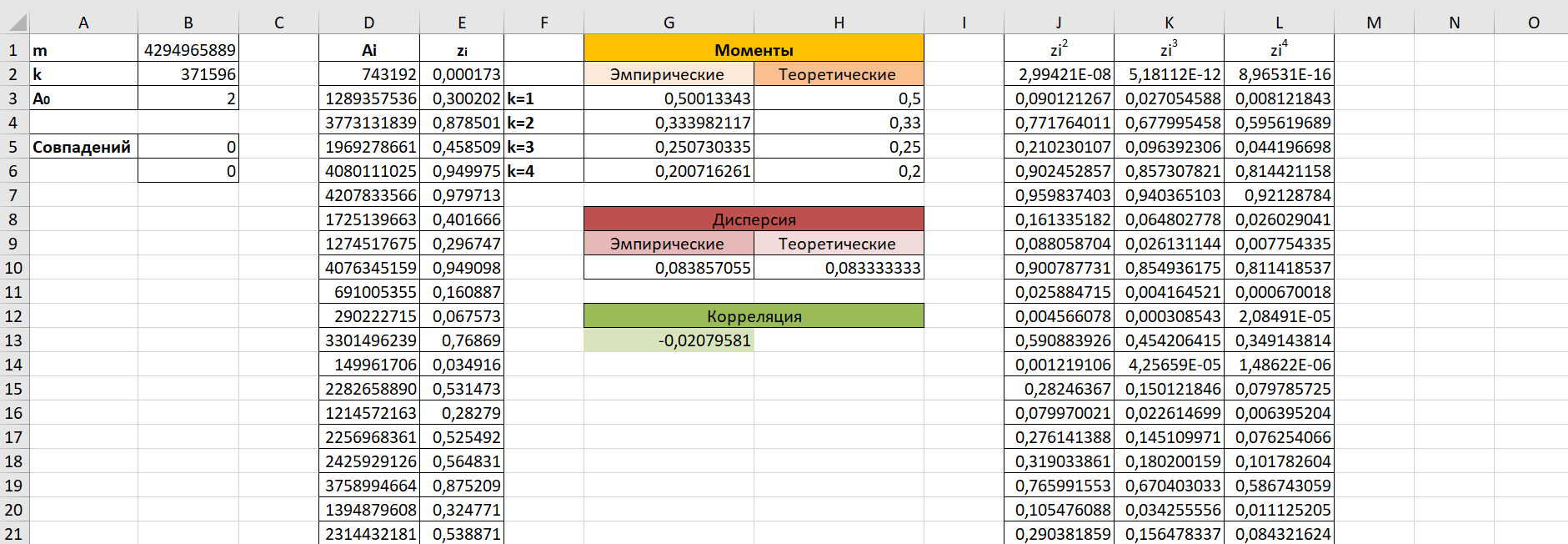

На рисунке 2 представлен вид рабочего листа в программе Excel.

Рисунок 2. Вид рабочего листа в Excel

2. 
   Метод построения эмпирической функции распределения вероятностей.
   

На Листе 2 проведем построение эмпирич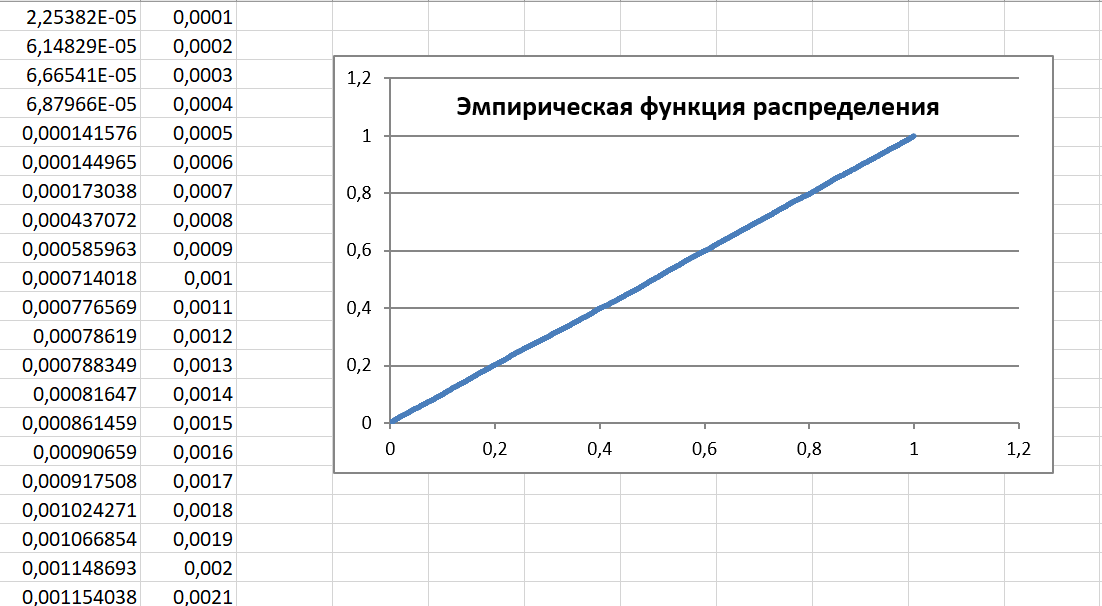еской функции распределения.

На рисунке 3 представлен вид эмпирической функции распределения.

Рисунок 3. Вид эмпирической функции распределения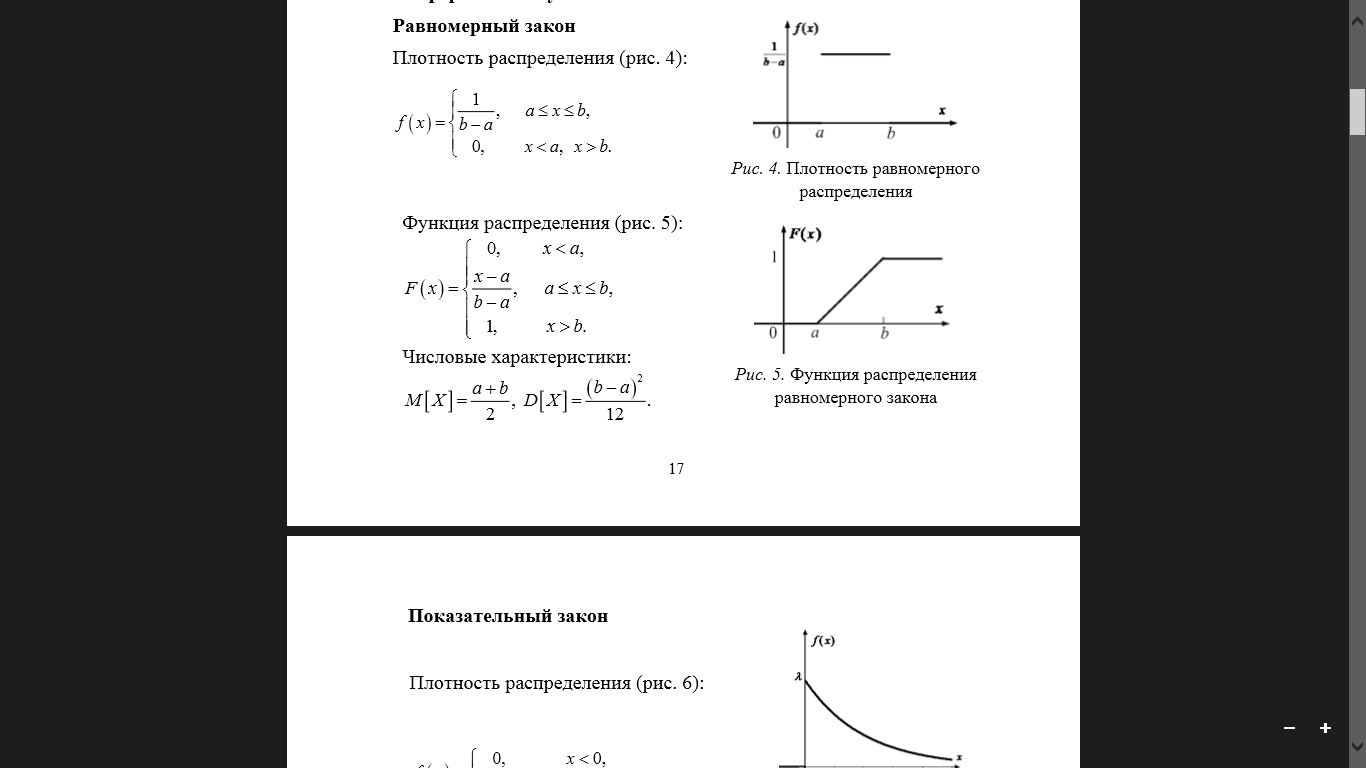




Рисунок 4. Теоретическая функция распределения
Как видно из рисунков 3 и 4 эмпирическая функция распределения полностью похожа на теоретическую, описываемую выражением F(t)=t (0≤t≤1).

4. 
   Тестирование датчика на независимость БСВ.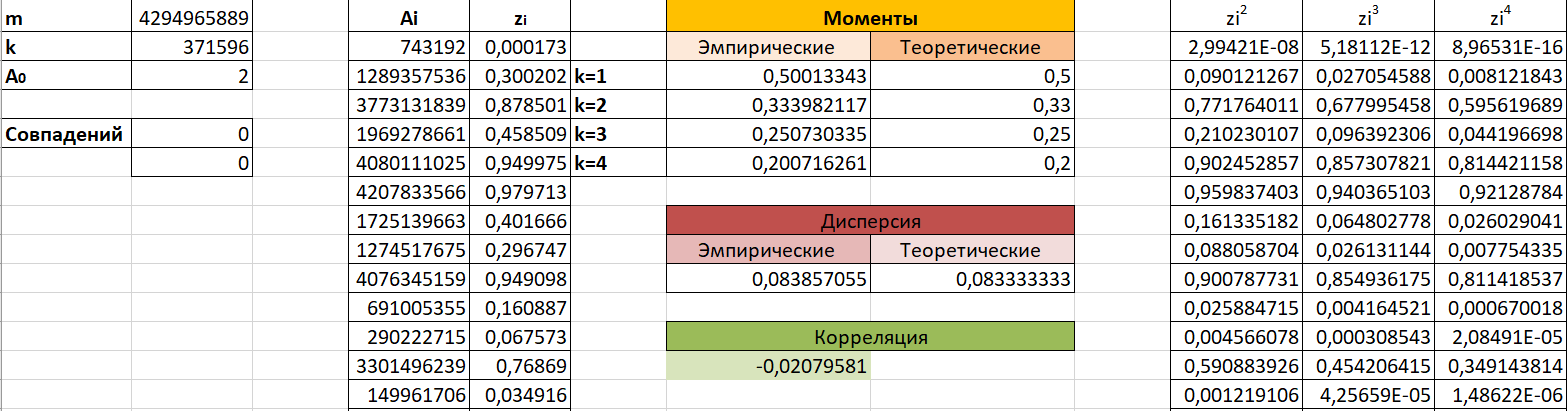
   

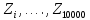Выполним проверку независимости псевдослучайных чисел , оценив коэффициент корреляции между двумя последовательно выдаваемыми датчиком числами. На рисунке 5 представлено нахождение коэффициента корреляции.

Рисунок 5. Коэффициент нахождения корреляции.

Так как коэффициент корреляции между парой соседних элементов выборки составляет -0,0208, то это свидетельствует об отсутствии зависимости между соседними элементами выборки.
Заключение

В ходе работы была смоделирована выборка из 10000 псевдослучайных чисел. Выборка была проверена на длину периода и установлено, что все элементы выборки – различны. Тестирование полученной выборки было осуществлено тремя методами, результат тестирования – выборка является случайной, равномерно-распределенной на интервале (0,1).

Список использованных источников

1. Задорожный В.Н., Маркова М.П. Информатика – методические указания к лабораторным работам. – Омск: Изд-во ОмГТУ, 2022. – 29 с.