Многокритериальная задача об упаковке в контейнеры. Задача об упаковке в контейнеры

• Название: Задача об упаковке в контейнеры
• Анкор: Многокритериальная задача об упаковке в контейнеры
• Дата: 02.05.2021
• Размер: 202.5 Kb.
• Имя файла: tasks1_2.doc
• Тип: Задача; #200883

Многокритериальная задача об упаковке в контейнеры

Общая постановка задачи

Пусть имеется М объектов, которые нужно упаковать в К контейнеров для перевозки, причём К<<М. Объект характеризуется количественными физическими параметрами (Р параметров), например, вес и объём. Контейнер характеризуется этими же параметрами, например, объём и грузоподъёмность. Кроме того, каждый объект имеет оценки по нескольким критериям, которые определяют его качество, привлекательность для лица, ответственного за перевозку (ЛПР). Каждый критерий имеет порядковую шкалу.

Задача решается при следующем условии:



где V^k, V^o – объёмы контейнеров и объектов соответственно.

Желательно осуществить упаковку так, чтобы:

1. 
   число упакованных объектов было бы максимально возможным, критерий О₁;
   
2. 
   среди упакованных объектов было бы максимально возможное количество таких, качество которых превосходило бы качество неупакованных объектов, критерий О₂.
   

(Вспомните проблему упаковки багажа при сборах в отпуск).

Для начала видоизменим задачу. Предположим, что имеющиеся М объектов нужно упаковать в минимально возможное число контейнеров. Эта задача является NP-полной и единственным гарантированно находящим оптимальное размещение методом решения является полный перебор. Однако есть ряд простых эвристических алгоритмов, дающих неплохой результат. Рассмотрим их.

1. 
   Алгоритм ПП – первый подходящий.
   

Объекты и контейнеры упорядочиваются произвольным образом. Объект кладётся в первый подходящий по физическим характеристикам контейнер.

2. 
   Алгоритм ППУ – первый подходящий с убыванием.
   

Объекты и контейнеры упорядочиваются по убыванию. Затем каждый объект также кладётся в первый подходящий по физическим характеристикам контейнер.

3. 
   Алгоритм ЛП – лучший подходящий.
   

Идея алгоритма аналогична алгоритму ПП с той разницей, что объект помещается не в первый подходящий, а в наиболее подходящий, т.е. в тот контейнер, где имеется наименьшее достаточное для него место.

4. 
   Алгоритм ЛПУ – лучший подходящий с убыванием.
   

Алгоритм аналогичен ЛП, но объекты упорядочены от меньших к большим.

Для этих алгоритмов получен ряд оценок для худших случаев:

1. 
   Алгоритм ППУ: пусть К₀ – минимальное достаточное для перевозки число контейнеров, полученное полным перебором; К_ппу – число контейнеров в соответствии с алгоритмом ППУ. Тогда для любого >0 и достаточно большого К₀ справедливо неравенство:
   

(1)

Т.о. решение ППУ отличается от оптимального не более чем на 23%.

2. 
   Алгоритм ПП: оценка хуже –
   

(2)

Для интуитивно лучших алгоритмов ЛП и ЛПУ математиками не найдено лучших оценок, чем для ПП и ППУ.

Формальная постановка задачи

Основные отличия реальной задачи об упаковке от упрощённой задачи:

• 
  объекты имеют оценки качества по многим критериям;
  
• 
  надо упаковать максимальное число объектов в фиксированное число контейнеров, а не фиксированное число объектов в минимальное число контейнеров.
  

Примем следующие обозначения: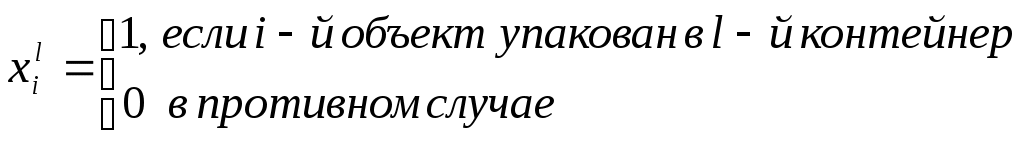



v_ji – j-й физический параметр i-го объекта;

V_jl – j-й физический параметр l-го контейнера;

U_i – общая ценность i-го объекта;

I=1,2,…,M;

I⁺={iI | jI : Uj  Ui, } – множество тех упакованных объектов, для которых не найдётся более ценных среди неупакованных.

Формальная постановка задачи имеет вид:

1. 
   количество упакованных объектов – максимально возможное:
   

(3)

2. 
   количество тех упакованных объектов, для которых не найдётся более ценных среди неупакованных, также стремится к максимуму: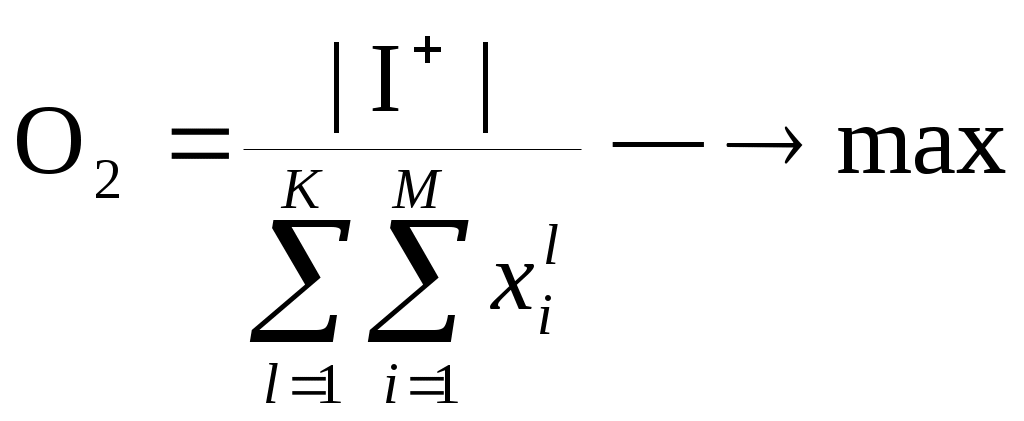
   

(4)

3. 
   сумма по каждому физическому параметру объектов, упакованных в l-й контейнер, меньше либо равна значению этого физического параметра для данного контейнера:
   

(5)

4. 
   каждый объект упаковывается только 1 раз:
   

(5)

Пусть N – количество критериев;

w_i – количество оценок на шкале i-го критерия, расположенных в порядке убывания;

Ai – множество оценок на шкале i-го критерия.

Тогда Y = A₁A₂…A_N – множество векторных оценок;

y_i = (y_i¹, y_i²,…y_i^N) – произвольная векторная оценка.

Алгоритм решения включает в себя алгоритмы решения вспомогательных задач:

1. 
   упаковка многомерных объектов в контейнеры;
   
2. 
   получение информации от ЛПР, позволяющей определить порядок упаковки многокритериальных объектов.
   

Рассмотрим вариант с равноценными объектами и алгоритм с отбрасыванием (АО). Цель – максимизировать количество объектов.

Применим алгоритм ППУ, разместим n первых объектов из списка (сколько поместится). Далее, если не поместились все объекты, отбрасывается самый тяжёлый (или объёмный) объект, и снова применяется алгоритм ППУ. Так делают до тех пор, пока список не будет исчерпан. В качестве решения выбирают тот вариант, у которого количество объектов больше.

Если физических параметров не один, а несколько, то объекты чередуются так: самый тяжёлый, самый объёмный, имеющий самые большие линейные размеры и т.д. Отбрасывание производится в соответствие с этим списком, и алгоритм называется алгоритм с отбрасыванием и чередованием (АОЧ).

Оценка алгоритма АО: M_max  7/6M_AO+3.

M_max – число объектов, найденное перебором.

Оценка алгоритма АОЧ, полученная экспериментальным путём: M_АОЧ/M_max = 0.95.

Общий алгоритм решения задачи об упаковке

1. 
   Предварительное упорядочивание объектов в соответствии с отношением доминирования.
   

Исследование соотношений по качеству объектов. Путём попарного сравнения объектов определяется асимметричное транзитивное отношение доминирования:

P⁰={(y_i,y_j)YY | k=1,…,N; y_i^k y_j^k и p: y_i^p< y_j^p }

2. 
   Выделение паретовых слоёв.
   

В соответствии с отношением P⁰ на множестве объектов можно выделить подмножество недоминируемых объектов. После их удаления можно выделить второе подмножество и т.д. до исчерпания множества. Выделенные слоя являются паретовыми слоями.

3. 
   Предварительная упаковка объектов.
   

Она заключается в применении алгоритма АОЧ по слоям.

Пусть упаковка объектов (i-1) первых слоёв возможна, но объекты i-го слоя уже не входят. Рассмотрим частный случай, когда каждый объект (i-1)-го слоя превосходит каждый объект i-го слоя и каждый объект i-го слоя в свою очередь превосходит каждый объект (i+1)-го слоя, причём объекты, принадлежащие одному слою, эквиваленты по качеству. В этом случае можно сразу переходить к шагу 6, т.к. имеется вся необходимая информация для упаковки объектов в месте их предполагаемого "разреза" на группы упакованных и неупакованных объектов.

В общем случае такая информация отсутствует. Для уменьшения неопределённости требуются шаги 4,5.

4. 
   Определение информации, требующейся для предварительного упорядочивания объектов.
   

Производится сравнение объектов (i-1), i и (i+1) слоёв, т.е. тех слоёв, где вероятно произойдёт разделение объектов при упаковке. Определяется объём информации, необходимый для упорядочения этих объектов по качеству.

Если объекты этих слоёв находятся в отношении доминирования или "почти" доминирования (т.е. доминирования по всем критериям, кроме одного), то информация для упорядочения этих объектов может быть получена от ЛПР путём прямого опроса. ЛПР предъявляют объекты (попарно) и выясняют, какой из них для ЛПР является более ценным. При возникновении противоречий (A>B>C>A) необходимо указывать на эти противоречия ЛПР для их разрешения.

В общем случае объекты отличаются оценками по нескольким критериям и при этом являются достаточно представительными элементами множества Y. Для их упорядочения требуется дополнительная информация о предпочтениях ЛПР.

Например, если все объекты можно расположить в соответствии с оценками так, как это приведено на рис. 3.1,а ,то объекты 2 и 5, 4 и 6, 4 и 7 оказываются несравнимыми. Для их упорядочения нужна дополнительная информация от ЛПР (рис. 3.1,б).

Методы прямого опроса в данной ситуации используются редко, т.к. это достаточно сложная для ЛПР операция выбора. Выявление предпочтений ЛПР осуществляется с помощью построения решающего правила ЛПР (мы рассмотрим это позже).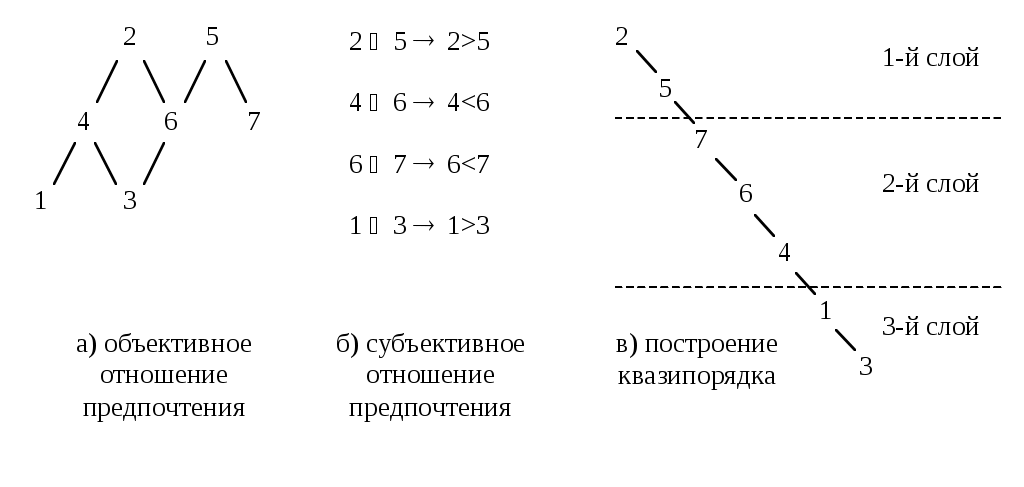



Рис. 3.1. Пример построения квазипорядка для объектов

5. 
   Построение квазипорядка на множестве объектов.
   

На основе сформированного на шаге 4 бинарного отношения можно построить квазипорядок (рис. 3.1,в) и выделить паретовые слои. При этом считается, что объект, принадлежащий высшему слою, "потенциально" лучше объекта из низшего слоя.

6. 
   Нахождение различных вариантов упаковки.
   

К построенному квазипорядку итеративно применяется алгоритм АОЧ. Среди объектов, упакованных на первом этапе, выделяется подмножество объектов, превосходящих каждый из остальных упакованных, если таковые имеются. Это подмножество подлежит обязательной упаковке. Далее к списку применяется алгоритм АОЧ, но объекты из вышеуказанного подмножества не отбрасываются. Т.о., алгоритм применяется, начиная с i-го слоя объектов.

Будем применять алгоритм АОЧ до исчерпания списка. Получим варианты с различными значениями критериев, например, для случая двух критериев (рис. 3.1):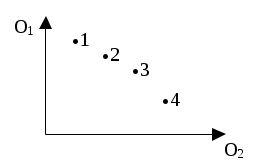



Рис. 3.1. Примеры оценок вариантов решений по двум критериям

7. 
   Определение компромисса между критериями (3) и (4).
   

ЛПР может выбрать один из полученных вариантов или указать соотношение значений критериев, по которому будет произведён этот выбор, например:

K = max (0.9O₁ + 0.3O₂)

Метод решения задачи об упаковке может быть распространён на случаи, когда:

1. 
   часть объектов может быть упакована только в определённые контейнеры;
   
2. 
   несколько объектов имеют общие части и должны быть упакованы вместе.
   

Многокритериальная задача о назначениях

Общая постановка задачи

В теории исследования операций эта задача формулируется как однокритериальная: для каждой работы известна её стоимость при выполнении каждым исполнителем. И критерий  минимизация суммарной стоимости выполнения. В реальности приходится учитывать много критериев.

Пусть имеется М субъектов и М объектов (задач, работ). Каждый субъект и каждая задача характеризуется оценками по N критериям (критерии, естественно, одни и те же). Необходимо назначить субъекта для исполнения каждой задачи с учётом значений оценок по критериям.

Шкалы оценок дискретные. Причина дискретности шкал в том, что многие критерии имеют качественный характер и могут быть выражены дискретными формулировками. Оценки на шкалах упорядочены от лучшей к худшей. Если _i – номер оценки на шкале j-го критерия, то при I=1 имеем худшую оценку.

Пусть имеется объект O_i с оценками O_i¹, O_i²,…, O_i^N и субъект C_j с оценками C_j¹, C_j²,…, C_j^N, где O_i^k, C_j^k – номера оценок на шкале k-го критерия. Определим j-ю компоненту вектора соответствия характеристик i-го субъекта требуемым характеристикам v-го объекта: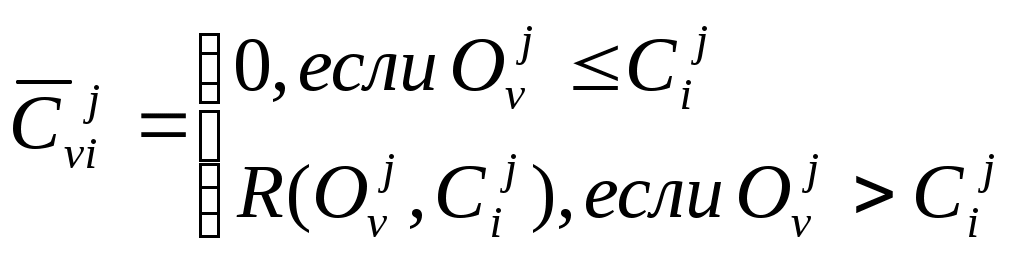

(1)

где R(O_v^j, C_i^j) – количество оценок на шкале j-го критерия, на которое O_v^j превышает C_i^j. Вектор 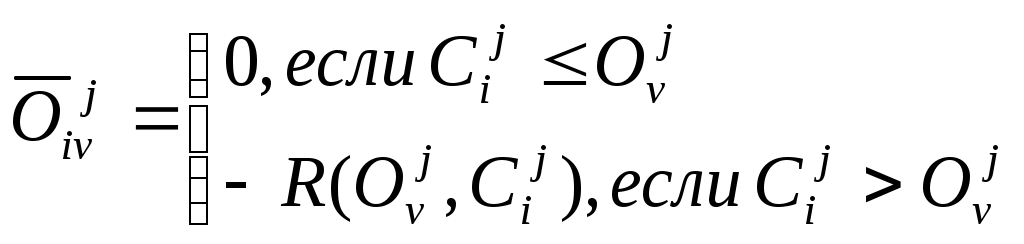определяет, насколько i-й субъект не удовлетворяет требованиям, предъявляемым v-м объектом. Определим аналогично:

(2)

как j-ю компоненту вектора, описывающего соответствие между характеристиками v-го объекта и требованиями i-го субъекта.

Формулы (1) и (2) соответствуют типичному для задачи о назначениях пониманию оценок объекта как уровня требований, предъявляемых к субъекту. Оценки субъекта рассматриваются как его возможности. Естественно, что после достижения уровня требований объекта оценки субъекта являются "одинаково хорошими" для объекта.

Решение задачи о назначениях

Для каждого v-го объекта могут быть найдены векторы соответствия ,…, . Введём следующее бинарное отношение (B1): вектор доминирует над вектором , если:

, j=1,2,…,N (3)

причём хотя бы для одной компоненты справедливо строгое неравенство (т.е. чем меньше несоответствие между оценками объекта и субъекта, тем лучше). Вектор эквивалентен вектору , если их компоненты равны:

, j=1,2,…,N (4)

Если не выполняется (3) и (4), вектора несравнимы.

В соответствии с бинарным отношением В1 на элементах ,…, может быть построен граф T_v, в котором дугой, направленной от к , отражается отношение доминирования (3), дугой с двумя противоположными стрелками – отношение эквивалентности (4), а отсутствие дуги говорит об отношении несравнимости.

Для i-го субъекта могут быть определены в соответствии с (2) векторы ,…, . Введём бинарное отношение В2 между этими векторами: вектор доминирует над вектором , если:

, j=1,2,…,N (5)

причём хотя бы для одной компоненты справедливо строгое неравенство. Вектор эквивалентен вектору , если их компоненты равны:

, j=1,2,…,N (6)

Если не выполняется (5) и (6), вектора несравнимы.

В соответствии с бинарным отношением В2 на элементах ,…, .может быть построен граф S_i, в котором дугой, направленной от к , отражается отношение доминирования (5), дугой с двумя противоположными стрелками – отношение эквивалентности (6), а отсутствие дуги говорит об отношении несравнимости.

Получим два графа подобия T_v и S_m.

Лемма: графы подобия не содержат циклов.

Анализ графов подобия

Этап I. Выделение в графе вершин, в которые не входят однонаправленные дуги. По сути, эти вершины либо доминируют над остальными, либо несравнимы с ними, т.е. составляют множество Парето в пространстве критериев. Назовём эти вершины ядром 1-й степени. Если элементы ядра несравнимы, присвоим им индекс Н1, если доминируют – Д1.

Этап II. Удалим из графа вершины ядра 1-й степени. Повторим для графа этап I, только ядру присвоим индексы 2 (Н2 и Д2).

Процесс выделения ядер продолжается до полного исчерпания вершин. Если остаётся две вершины, то им присваивается индекс Дi, если они эквивалентны или если все вершины (i-1)-го ядра доминируют над вершинами i-го ядра.

Если провести подсчёт вероятностей того, что между двумя вершинами графа подобия будет отношение доминирования или эквивалентности (при условии равновероятности получения оценок), то получаются высокие значения. Так, при шести критериях с тремя оценками вероятность доминирования одной вершины над другой 0.52. Это позволяет предположить, что реальные графы подобия имеют большое количество дуг.

Формирование матриц сходства

На основе анализа графов подобия формируется матрица сходства (рис. 3.2).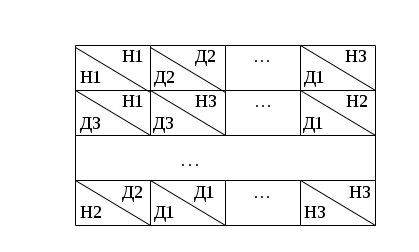



Рис. 3.2. Матрицы сходства графов подобия

В каждой ячейке матрицы сходства содержится два значения: над чертой – оценка субъекта со стороны объекта, под чертой – оценка объекта со стороны субъекта.

Для матрицы сходства возможны три случая:

1. 
   Есть одна ячейка Д1\Д1. Тогда производится "идеальное назначение" O_v – C_i, и эти вершины удаляются из дальнейшего рассмотрения.
   
2. 
   Есть несколько ячеек Д1\Д1. Если они находятся в разных строках и столбцах, то производится несколько "идеальных назначений". Если ячейки Д1\Д1 находятся в одной строке (столбце), производится одно из возможных "идеальных назначений", после чего назначенные вершины удаляются из рассмотрения.
   
3. 
   В матрице нет ни одной ячейки Д1\Д1. В этом случае необходимо обратиться в ЛПР за дополнительной информацией. Эта информация нужна для установления новых связей (дуг) в графе. Для этого анализируются клетки Д1\Н1, Н1\Д1 и Н1\Н1. ЛПР предъявляются вектора соответствия, получившие индекс Н1, и другие вектора из этого же графа и ставится вопрос: какой из векторов лучше (является доминирующим)? Ответ на этот вопрос позволяет провести в графе дополнительные дуги и изменить матрицу сходства. (Ответы ЛПР необходимо проверять на отсутствие противоречий).
   

После удаления вершин, для которых проведены назначения, из оставшихся вершин строятся графы подобия, и всё повторяется (до исчерпания списка вершин).

Оценим вышеприведённый способ решения задачи о назначениях с точки зрения сложности выполняемых ЛПР операций. ЛПР осуществляет формирование шкал критериев (021) и сравнивает формально несравнимые альтернативы (031). Первая операция является допустимой, вторая  сложной, т.е. в целом метод можно оценить как сложный для ЛПР. С другой стороны, реальные вектора соответствия часто отличаются друг от друга оценками по одному-двум критериям. Расчёт вероятностей того, что вектора соответствия отличаются по 1-2 критериям, показывает следующую тенденцию: эта вероятность увеличивается при увеличении количества критериев и размерности шкал критериев. Например, вероятность для 5 критериев и 3-х балльных шкалах составляет 0.36, а для 4-х балльных шкал  0.43. Таким образом, для оценки ЛПР предъявляются обычно вектора, отличающиеся значениями 1-2 критериев. Сравнить такие вектора несколько проще, чем вектора, несравнимые по 3-м и более критериям.

Рассмотренный метод решения задачи о назначениях чувствителен к ошибкам ЛПР (БЧ), но обеспечивает сходимость процесса. Целесообразность применения этого метода заключается в том, что система сама выявляет объективные соответствия требований задач и возможностей исполнителей, уменьшая объём задачи, которую должен решить ЛПР, и гарантируя получение лучшего решения, чем при случайном распределении работ. Отметим, что возможны ситуации, когда применение данного метода не требует от ЛПР выполнения сложных операций (если в каждой строке матрицы сходства графов подобия найдётся одна ячейка Д1\Д1).