Лаб 1 Физика. Введение Целью настоящей работы является изучение кристаллического строения твердых тел и дифракции рентгеновского излучения в кристаллах.
 Скачать 63.9 Kb. Скачать 63.9 Kb.
|
|
Введение Целью настоящей работы является изучение кристаллического строения твердых тел и дифракции рентгеновского излучения в кристаллах. В ходе выполнения данной работы необходимо рассчитать углы отражения от плоскостей 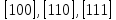 и определить относительную интенсивность максимума для указанных плоскостей с учетом плотности заполнения плоскости атомами, фактора поглощения, фактора повторяемости и температурного фактора, а также графически изобразить вид дифрактограммы в координатах интенсивность-угол отражения. и определить относительную интенсивность максимума для указанных плоскостей с учетом плотности заполнения плоскости атомами, фактора поглощения, фактора повторяемости и температурного фактора, а также графически изобразить вид дифрактограммы в координатах интенсивность-угол отражения.Задание Найти углы отражения от плоскостей 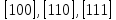 кристалла кристалла 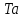  , соответствующие дифракционным максимумам , соответствующие дифракционным максимумам  -ого порядка для характеристического рентгеновского излучения -ого порядка для характеристического рентгеновского излучения 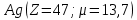 : :а) учитывая, что интенсивность дифракционного максимума зависит от плотности заполнения плоскости атомами, фактора поглощения, фактора повторяемости и температурного фактора, определить относительную интенсивность максимума для указанных плоскостей; б) графически изобразите вид дифрактограммы в координатах интенсивность – угол отражения. Расчетная часть Для расчета углов отражения воспользуемся условием Вульфа-Брэгга: 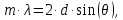 где 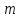 – номер дифракционного максимума; – номер дифракционного максимума; 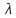 – длина волны характеристического рентгеновского излучения, – длина волны характеристического рентгеновского излучения, 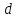 – межплоскостное расстояние, – межплоскостное расстояние, 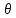 – угол отражения рентгеновского излучения. – угол отражения рентгеновского излучения.Длину волны характеристического излучения определим из закона Мозли: 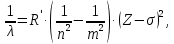  где  – постоянная Ридберга, – постоянная Ридберга, 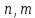 – целые числа – целые числа 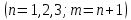 , , 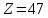 – порядковый номер серебра – порядковый номер серебра 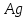 в периодической таблице Менделеева, в периодической таблице Менделеева,  – постоянная экранирования. – постоянная экранирования. Межплоскостное расстояние рассчитаем по формуле: 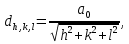 где 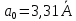 – постоянная кристаллической решетки тантала – постоянная кристаллической решетки тантала 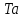 , , 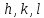 – индексы Миллера. – индексы Миллера.Для плоскости 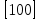 : :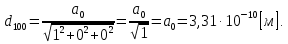 - для плоскости 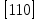 : :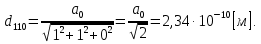 - для плоскости 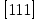 : : Выразим углы отражения из условия Вульфа-Брэгга: 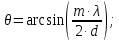 Для плоскости 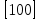 : :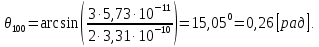 - для плоскости 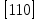 : : - для плоскости 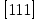 : :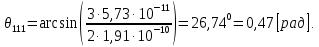 Под действием рентгеновского излучения электроны в твердом теле совершают вынужденные колебания и вследствие этого становятся источниками электромагнитных колебаний той же частоты. Полная интенсивность рассеяния электронов в заданном направлении в рамках кинематической теории выражается формулой:  где  – заряд электрона, – заряд электрона,  – масса электрона, – масса электрона,  – скорость света в вакууме, – скорость света в вакууме,  – расстояние от рассеивающего центра до плоскости, – расстояние от рассеивающего центра до плоскости, 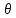 – угол отражения. – угол отражения.Рассчитаем сомножитель: 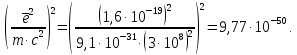 Так как в твердом теле количество электронов 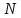 , то выражение для интенсивности рассеяния электронов примет вид: , то выражение для интенсивности рассеяния электронов примет вид: Количество электронов 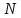 определим из соотношения: определим из соотношения: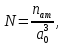 где 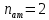 – количество атомов, приходящихся на одну элементарную ячейку в кубической объёмно-центрированной решетке. – количество атомов, приходящихся на одну элементарную ячейку в кубической объёмно-центрированной решетке. Учтем, что интенсивность зависит от плотности заполнения плоскости атомами. Это можно учесть с помощью коэффициента компактности: 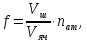 где 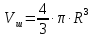 – объем жестких сфер, – объем жестких сфер,  – объем элементарной ячейки. – объем элементарной ячейки. В кубической объемно-центрированной ячейке (ОЦК) шары соприкасаются по телесной диагонали куба, то есть длина телесной диагонали равна  , а параметр ячейки , а параметр ячейки 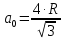 , а на ячейку ОЦК приходится два шара, тогда: , а на ячейку ОЦК приходится два шара, тогда: Так как требуется найти относительную интенсивность, то:  Фактор поглощения  учитывает ослабление рентгеновского излучения в образце при данной геометрии и зависит от линейного коэффициента поглощения: учитывает ослабление рентгеновского излучения в образце при данной геометрии и зависит от линейного коэффициента поглощения: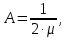 где  – линейный коэффициент поглощения для хрома. – линейный коэффициент поглощения для хрома.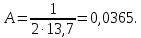 Перепишем выражение для относительной интенсивности: 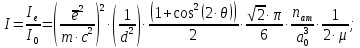 Вероятность появления в отражающем положении той или иной грани кристалла выражается фактором повторяемости 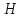 . Множитель . Множитель 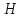 пропорционален числу эквивалентных кристаллографических плоскостей, образующих кристаллическую форму, и выражается целыми числами. Для плоскости пропорционален числу эквивалентных кристаллографических плоскостей, образующих кристаллическую форму, и выражается целыми числами. Для плоскости 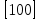  , для плоскости , для плоскости 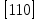  , для плоскости , для плоскости 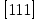 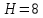 , то есть , то есть 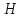 равен количеству повторений грани куба. равен количеству повторений грани куба. Тогда исследуемое выражение с учетом фактора повторяемости запишем следующим образом: 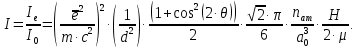 Температурный множитель учитывает разность фаз рассеянных рентгеновских лучей, возникшую вследствие тепловых колебаний:  где 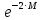 – температурный множитель. – температурный множитель.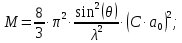 Для плоскости 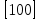 : :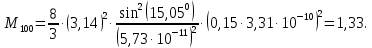 - для плоскости 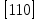 : : - для плоскости 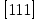 : :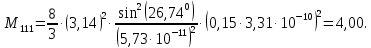 Общее выражение для определения зависимости относительной интенсивности от угла отражения с учетом всех факторов имеет вид: 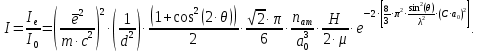 Для плоскости 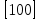 : :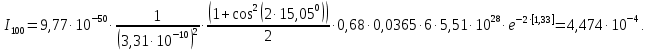 - для плоскости 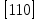 : :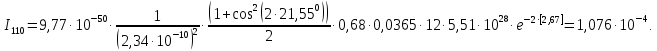 - для плоскости 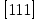 : :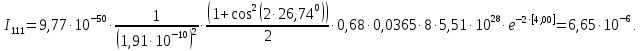 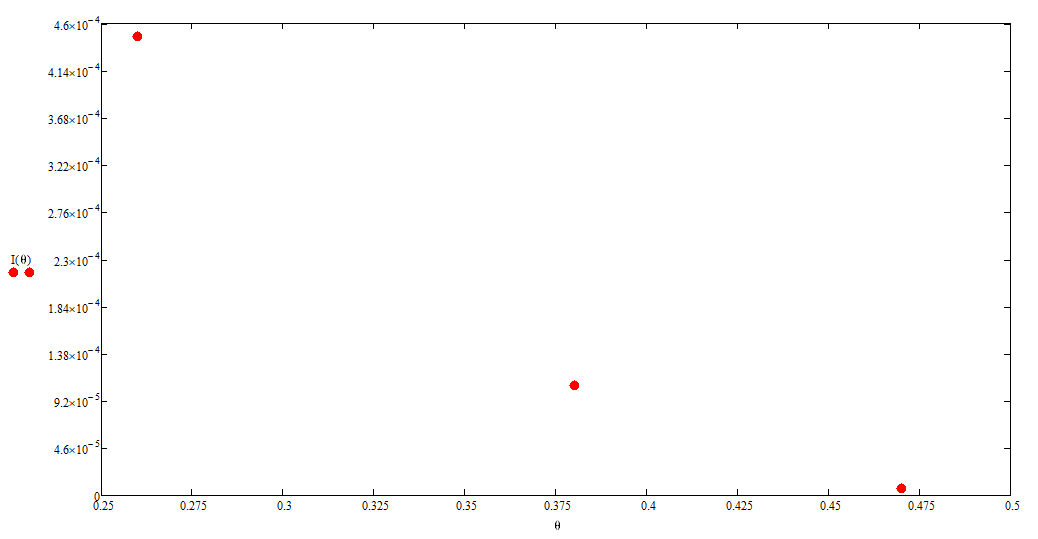 Вид дифрактограммы в координатах интенсивность-угол отражения для рассчитанных значений относительной интенсивности Заключение В ходе выполнения данной работы рассчитаны углы отражения от плоскостей 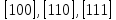 и определена относительная интенсивность максимума для указанных плоскостей с учетом плотности заполнения плоскости атомами, фактора поглощения, фактора повторяемости и температурного фактора, а также графически изображена дифрактограмма в координатах интенсивность-угол отражения. и определена относительная интенсивность максимума для указанных плоскостей с учетом плотности заполнения плоскости атомами, фактора поглощения, фактора повторяемости и температурного фактора, а также графически изображена дифрактограмма в координатах интенсивность-угол отражения.Список литературы 1 Смирнов, С.В. Физика твердого тела: Учебное пособие. – Томск: Изд-во НТЛ, 2003, – 276 с. 2 Саврук Е. В., Смирнов С. В. Физика конденсированного состояния: методические указания по лабораторным работам для студентов направления подготовки 210100.62 «Электроника и наноэлектроника», профиль «Промышленная электроника». — Томск: Факультет дистанционного обучения, ТУСУР, 2015. — 59 с. |
